考虑徐(温)变效应的列车与连续梁－框架墩桥耦合振动分析＊

苗永抗，尹邦武，郭向荣

(中南大学土木工程学院，湖南 长沙 410075)

客运专线铁路曲线半径大、技术标准高，与既有铁路、道路、管线等小角度交叉常常不可避免。用小跨度梁和框架墩结构代替常规大跨桥梁结构跨越，能有效降低结构高度，节省工期和造价，具有明显的技术经济优势。目前，框架墩－简支梁在速度不超过160 km/h的铁路上应用较多，但在铺设无砟轨道的客运专线桥梁上的应用尚缺乏研究［1］。本文主要分析徐(温)形变对客运专线连续梁－框架墩桥列车走行性的影响。

1 工程概况

某客运专线为7×16 m七跨等截面连续梁－框架墩桥，设计活载为ZK活载。本桥因需跨既有铁路线，墩采用了独柱墩与框架墩结合的方式。主梁采用单箱单室截面，梁高2 m，主梁采用C50混凝土，设纵向、横向和竖向预应力。框架墩垂直于既有线布设，与正线的法线夹角取15°，框架墩的横向跨度为20 m，承台角距离线路中心最小4.5 m。连续梁两端分别与20 m跨度的简支梁相连。既有线轨顶高程为2.19 m，既有线轨面到横梁底距离为11.0 m。全桥俯视图如图1所示。

图1 全桥俯视图Fig.1 A plan view of the full bridge

2 连续梁－框架墩徐(温)变形组合曲线

温度变化一方面使箱梁产生均匀变形，另一方面在箱梁内外形成较大的温度差，混凝土箱梁的各部分处于不同温度状态，将产生不同的温度变形。国内已经对引起这种变形的温度场做了部分研究［2，3］。由于本次分析桥梁主梁及框架墩均为箱型断面，这种温度变化引起的变形将会影响更大，并且桥梁设计时速为350 km/h公里，故非常有必要对连续梁－框架墩体系温度变形行为及对车桥动力响应的影响进行深入研究，为在时速350 km/h客运专线无砟轨道铁路桥梁上采用框架墩体系积累经验。

我国铁路规范TB 10002.3－2005关于日照下箱梁温度梯度的规定考虑了大气透明度、地理纬度、箱梁横向温差等因素。

日照下混凝箱梁沿梁高、梁宽方向的温度梯度按下式计算，见图2。

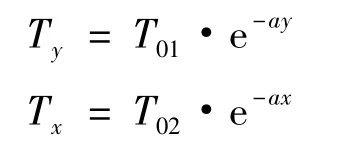
式中:Tx和Ty分别为计算点y和x处的温差(℃);T01和T0平分别为箱梁梁高方向、梁宽方向温差，可按表1取值;y和x分别为计算点至箱梁外表面的距离(m);a为参数，见表1。

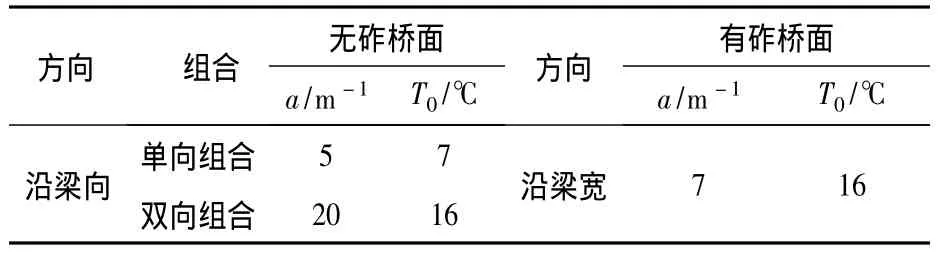
表1 日照温差曲线参数与温差值Table 1 The parameters and temperature values of sunshine temperature curve

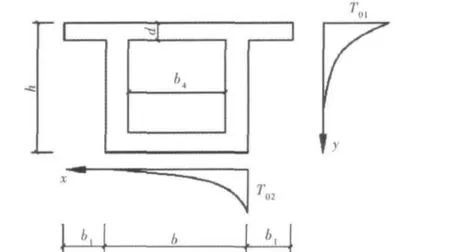
图2 箱梁温差分布图Fig.2 The temperature distribution of box girder

对于降温作用下的温度梯度，箱形梁沿顶板、外腹板板厚温差曲线的指数值a采用14 m，相应的T0采用－10℃。

对于该桥的温度取值，主要根据设计院提供的资料，选择以下参数:(1)合拢温度取5～10℃，结构整体升、降温按均匀升温25℃、降温20℃计算;(2)非线性温度变化，按TB10002.3－2005(《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》)附录B取值，组合说明如表2。

表2 温度组合Table 2 The combinations of temperatures

考虑徐变对列车走行性的影响，计算1500 d之后混凝土的徐变参与组合［4，5］。选取中间三个框架墩为一联连续梁的多固定墩体系。具体组合曲线说明如表3所示，组合曲线如图3所示。

为了说明徐(温)变的影响，本文还计算了在不考虑徐(温)变形情况下的车桥动力响应数据。

表3 组合曲线说明Table 3 The descriptions of combination curves

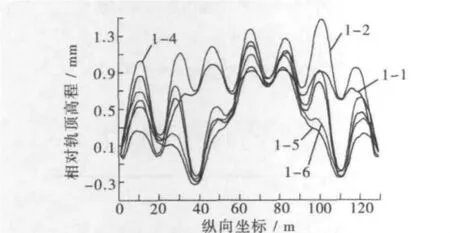
图3 各组合桥面相对变形曲线Fig.3 The deformation curves of deck related different combinations

3 车桥耦合振动分析

3.1 车桥动力响应研究的内容

(1)桥梁结构在列车动荷载作用下的强度问题，通常采用冲击系数来表达，其目的是为桥梁结构的动力设计提供参数。

(2)桥上列车的安全性问题，主要通过对轮轨力(轮重减载率、脱轨系数、横向力)的限制来保证行车安全。

(3)桥上行车的乘坐舒适度问题，以车体振动加速度和Sperling舒适度指标来反映。

3.2 空间振动方程的建立和求解

本文在研究空间振动方程时，首先运用达朗伯原理建立车桥系统运动方程，将列车与桥梁视为一个耦合的整体体系，然后采用曾庆元院士提出的“动力学势能不变值原理［6］”与形成矩阵的“对号入座［7］”法则建立桥梁刚度、质量、阻尼等矩阵，形成系统的空间振动矩阵方程:

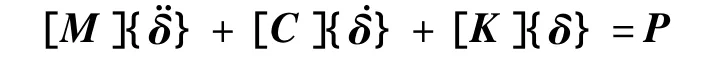
采用中南大学自主研发的列车桥梁时变系统空间振动分析软件TBI，进行车桥耦合振动分析，建立有限元模型如图4所示。

图4 有限元划分示意图Fig.4 The finite element model of the bridge

根据前述计算模型与计算原理，本文对全桥模型进行了分析计算，采用德国ICE3动力分散独立式高速列车，列车编组为“2×(动车+动车+拖车+动车+动车+拖车+动车+动车)”，计算速度等级取 160 km/h～420 km/h，(设计速度为350 km/h，取20%的检验速度)，轨道不平顺采用德国低干扰谱。

3.3 桥梁空间动力响应

首先，提供在不同工况下桥梁的最大冲击系数(表4)，以供设计参考。根据《铁路桥涵设计基本规范》中第 4.3.5 节内容，

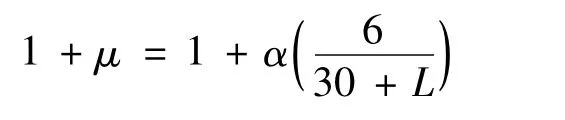
式中:α=4(1－h)≤2;h为顶板至轨底的填土厚度(m);L为连续梁跨度(m)。设h=0 m，α=2 m，L=16 m。由此可得1+μ=1.25。规范计算出的冲击系数比软件计算的略大，说明按照规范设计的桥梁荷载略大，计算结构偏于安全，规范取值是合理的。同时各工况冲击系数的最大值都出现在350 km/h时速下，说明该桥在列车以350 km/h通过时产生共振，并且单线冲击系数普遍比双线要高，这说明在两辆列车相对开出时，列车对桥梁作用产生折减。

表4 不同工况下桥梁最大冲击系数Table 4 The maximum impact coefficient of the bridge in different combinations

为了体现不同车速下桥梁的动力响应，图5和图6给出了各工况下双线列车以不同车速通过桥梁时，桥梁跨中横、竖向位移从图5和图6可以看出:徐(温)变形对连续梁－框架墩的车桥振动影响较大，尤其对桥梁横向位移产生较大影响，并且桥梁产生最大位移响应所对应的车速发生改变，应予以重视。同时还可以看出徐(温)变形对连续梁－框架墩的车桥振动影响随所采用的桥面组合变形曲线的不同而变化不敏感。

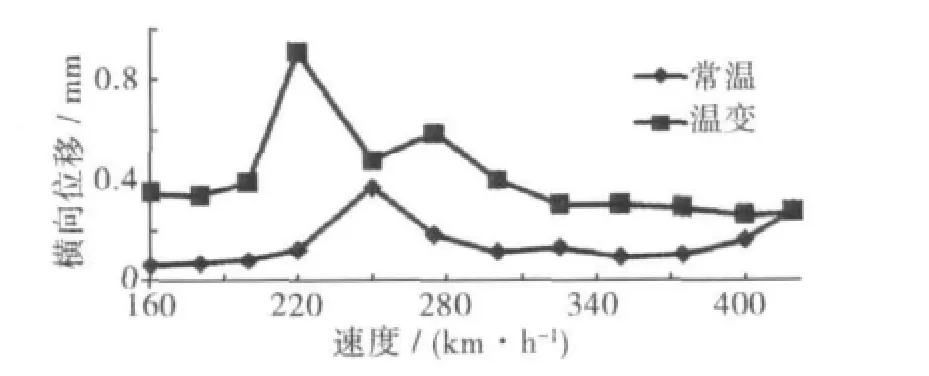
图5 不同时速下桥梁最大横向位移Fig.5 The maximum lateral displacement of the bridge in different speeds

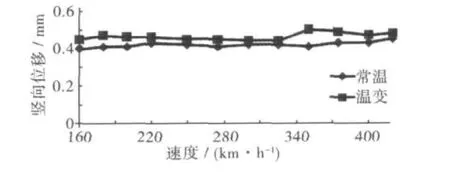
图6 不同时速下桥梁最大竖向位移Fig.6 The maximum vertical displacement of the bridge in different speeds

为了显示桥梁在列车通过过程中的振动情况，图7和图8分别为德国ICE3高速列车以350 km/h通过桥梁时，跨中横向位移和竖向位移的时程曲线。曲线表明，桥梁横、竖向位移值均不大，且在列车通过时产生多次均匀性波动，说明等截面连续梁在跨度16m的框架墩上的整体工作性良好，列车以较快速度通过时，并未产生某一个突出的最值点。

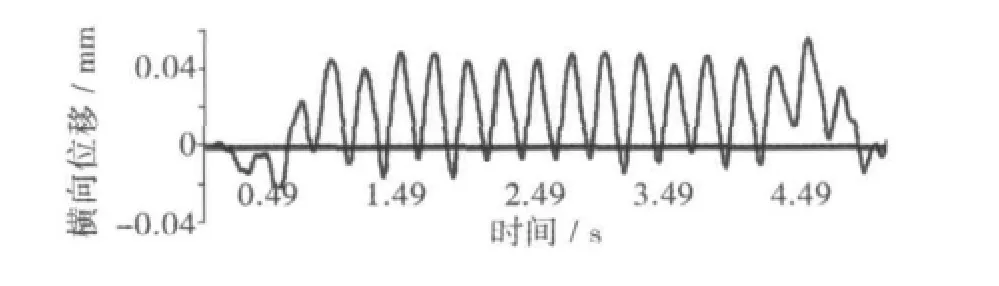
图7 350 km/h时跨中横向位移时程曲线Fig.7 Time history curve of midspan lateral displacement at train speed of 350 km/h

图8 350 km/h时跨中竖向位移时程曲线Fig.8 Time history curve of midspan vertical displacement at train speed of 350 km/h

从以上分析可以看出:列车在通过连续梁－框架墩时，受徐(温)变形的激励，会对桥梁产生较大的冲击力，使得桥梁位移增大。这种横、竖向振幅满足《铁路桥梁检定规范》［8－9］要求，该桥梁横、竖向刚度满足要求。

3.4 列车动力响应及其舒适性分析

分析列车安全性，主要分析脱轨系数、轮重减载率以及横向摇摆力。根据文献［8－9］中的规定，列车运行安全性的评价限值为:脱轨系数小于等于0.8，轮重减载率小于等于0.6，横向摇摆力小于等于80 kN。表5反应脱轨系数、轮重减载率及摇摆力在各种工况下的最大值。

表5 各工况下车辆安全性指标最大值Table 5 The maximum indicators of vehicle safety in different conditions

通过表5可以得出:高速列车在徐(温)变形下的连续梁－框架墩桥梁上运行时，依然满足行车的安全性。徐(温)变形对列车高速行驶时的轮重减载率影响较大，对脱轨系数和横向力的影响较小，而随所采用的桥面组合变形曲线的不同而变化不敏感。

为显示列车在不同时速下的安全情况，给出了在工况1－1下，动车脱轨系数、轮重减载率及横向力随速度的变化曲线，见图9。从图9可以看出:这几个参数都是随车速的增长而增长，当车速较大时，这种增长更加明显，在连续梁－框架墩用于高速铁路建设中对徐(温)变形应予以足够重视。

分析列车舒适性，我国客车运行平稳性(即舒适性)分别按平稳性指标和平均最大振动加速度来评定。根据文献［8－9］中的规定，列车运行平稳性指标为:进行车桥耦合振动计算分析中所得到车体最大竖向加速度容许值为0.13 g，横向为0.10 g。适合本文的Sperling舒适度指标限制为3.0。将列车的横、竖向加速度和横、竖向Sperling舒适性指标见表6。

通过表格中数据可知，列车在徐(温)变形下的连续梁－框架墩桥梁上行走时，舒适性满足要求。徐(温)变形对列车舒适性影响较大，而随所采用的桥面组合变形曲线的不同而变化不敏感。

同样，为显示列车在不同时速下的舒适情况，给出工况1－1下，动车竖向加速度、横向加速度及横、竖向Sperling指标随速度的变化曲线，见图10。

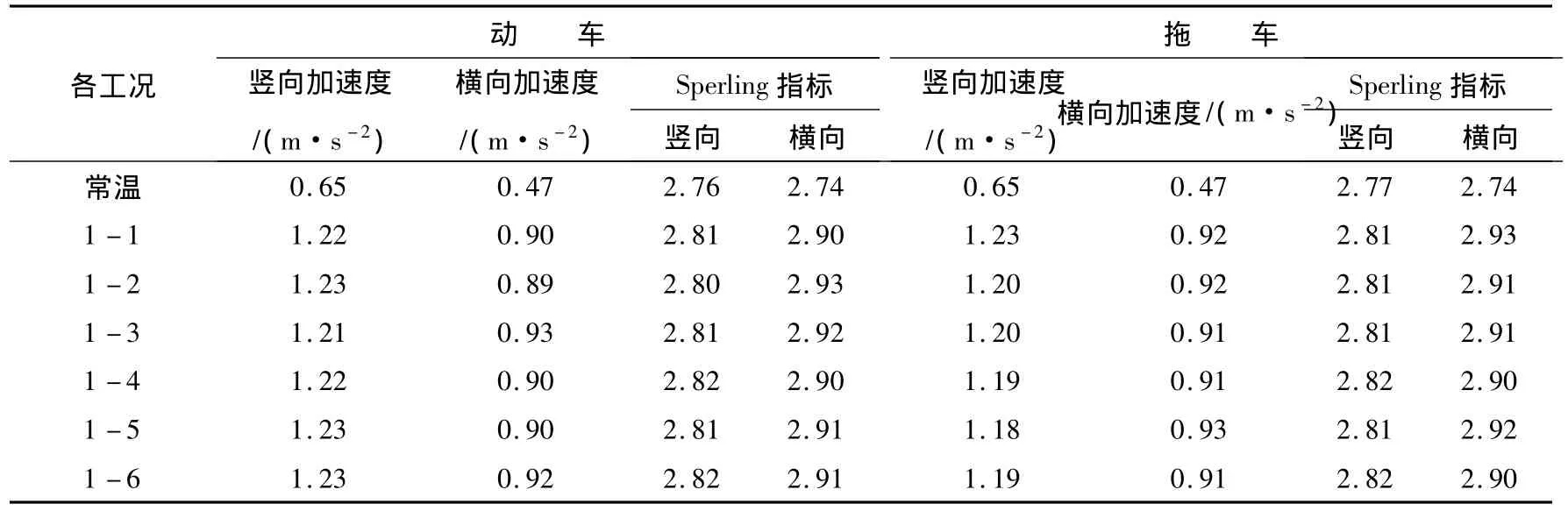
表6 各工况下车辆平稳性指标最大值Table 6 The maximum indicators of vehicle stationarity in different conditions

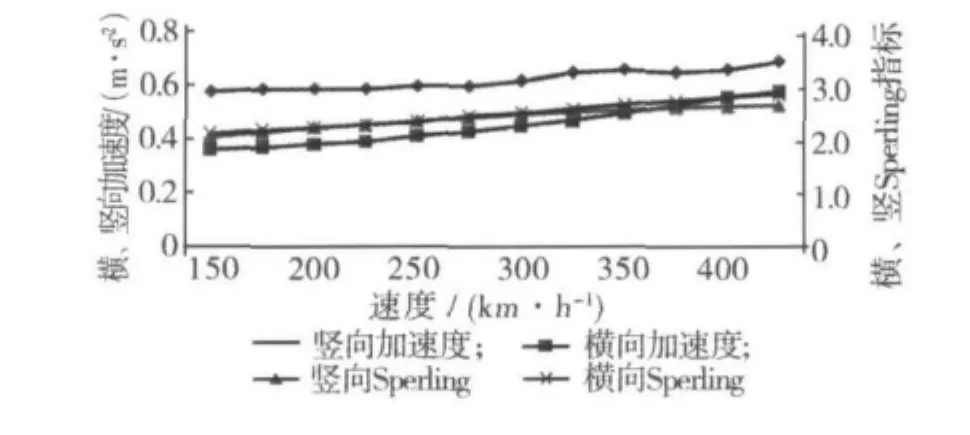
图10 不同时速下动车横竖向加速度及横竖向Sperling指标变化曲线Fig.10 The lateral and vertical acceleration and the Sperling index curves of the EMU in different speeds

4 结论

(1)各工况下，考虑徐(温)变形引起的桥面不平顺的桥梁响应值比未考虑其影响的值较大，而随所采用的桥面组合变形曲线的不同而变化不敏感。

(2)在所计算工况下，桥梁响应和车辆响应均在允许范围之内。车辆横向加速度及横向Sperling舒适度指标接近允许值，说明徐(温)变形引起的轨道不平顺属于长波不平顺，列车高速行驶时，更多的是会对车辆的影响。

(3)列车在各工况下响应值随车速增长而增长，当车速较大时，这种增长更加明显，因此，温度变形引起的桥面线路不平顺对列车走行性的影响必须予以足够重视。

［1］余常俊.客运专线连续梁－框架墩体系几个问题的探讨［J］.铁道标准设计.2012，2(2):100 －102.YU Changjun.Discussion of continuous beam －framework pier bridge in the using of passenger line［J］.The Standards of Railway Design.2012(2):100－102.

［2］范立础.预应力混凝土连续梁桥［M］.北京:人民交通出版社，1988:253－261.FAN Lichu.Prestressed concrete continuous beam bridge［M］.Beijing:People’s Transports Press，1988:253 －261.

［3］刘兴法.混凝土结构的温度应力分析［M］.北京:人民交通出版社，1991:46－103.LIU Xingfa.Thermal stress analysis of concrete structures［M］.Beijing:People’s Transports Press，1991:49 －103.

［4］向小斌.桥梁结构混凝土徐变试验研究［J］.交通科技，2007，4(2):20 －22.XIANG Xiaobin，Experiment in the concrete creep of bridge structure［J］.Science and Technology of Transport，2007，4(2):20 －22.

［5］胡狄，陈政清.从短期试验结果预测新建预应力混凝土梁收缩和徐变的长期效应［J］.中国铁道科学，2003，6(3):44－49.HU Di，CHEN Zhengqing.The long－ term forecasting of concrete creep and shrinkage efforts of new bridge from the short－ term experiment［J］.China Railway Science.2003，6(3):44 －49.

［6］曾庆元，郭向荣.列车桥梁事变系统振动分析理论与应用［M］.北京:中国铁道出版社，1999.ZENG Qingyuan，GUO Xiangrong.Theory and application of train－bridge time－variant system vibration analysis［M］.Beijing:China Railway Press，1999.

［7］曾庆元，杨平.形成矩阵的“对号入座”法则与桁段有限元法［J］.铁道学报，1986，8(2):48－59.ZENG Qingyuan，YANG Ping.The“set－in－right－position”rule for formulating matrix and the truss finite element method for spatial truss analysis［J］.Journal of the Railway Society，1986，8(2):48－59.

［8］GB 5599—85，铁道动力性能评定和试验鉴定规范［S］.GB 5599－85，The assessment and test norms of railway dynamic performance［S］.

［9］TB/T 2360—1993，铁道机车动力学性能试验鉴定方法及评定标准［S］.TB/T 2360—1993，The test and assessment standards of railway locomotive dynamic performance［S］.