钢轨在动载荷作用下的动应力响应特性分析＊

曹玉，黄志辉，李屹罡，杨星星

(1.中南大学机电工程学院，湖南 长沙 410083;2.高性能复杂制造国家重点实验室，湖南 长沙 410083)

研究钢轨在移动车轮作用下的动应力响应［1］对动态轨道超偏载检测［2］具有重要意义，因为一种常用的轨道超偏载检测方法是通过检测车轮经过钢轨时钢轨的动应力响应来实现的。文献［3］研究了使用应力检测法实现轨道超偏载检测的方法，但未对钢轨的动应力响应分布规律进行研究，未能将应力传感器安装在应力响应较大的位置，导致提取到的应力响应值较小，使得后续信号放大电路的放大倍数过大，得到信号的信噪比较低。为解决此问题，本文作者研究钢轨在车轮动载荷作用下的动应力响应规律，确定轨道超偏载检测传感器安装的合理位置。已有许多学者研究了钢轨受载时的动力响应规律，有很大的参考价值，但不能有针对性地解决文献［3］中所遇到的问题。例如:黄志辉等［4］应用有限元法分析钢轨受静态载荷下的应力分布场，得到钢轨在静载荷作用下的应力分布规律;Mazilu［5］应用格林函数研究轮轨模型在竖直激励下的动力响应，但未研究轮轨模型在移动载荷激励下的动力响应;黄志辉等［6］应用振型叠加法法对钢轨在移动载荷作用下的动力响应进行研究，得到简化梁在移动载荷作用下的动力响应，但对模型进行较大简化，且未研究钢轨在移动载荷下的动应力响应分布与变化规律。本文利用轨道弹射实验台提供的模拟轨道，运用非线性有限元分析软件ABAQUS提供的显式动力学分析法［7］，分析钢轨在移动载荷作用下的动应力响应。同时在实验台钢轨侧面粘贴应变片，用以模拟超偏载检测所使用的应力传感器，提取实验台钢轨在车轮动载荷作用下的应力响应数据，验证了有限元分析结果。综合有限元分析和实验分析得到钢轨侧面在车轮动载荷作用下的应力分布与变化规律，找到了最大应力响应点，得到了合理的超偏载检测应力传感器的安装位置，提高了超偏载检测信号的信噪比。

1 轨道弹射实验台模型

1.1 轨道弹射实验台物理模型

图1 轨道弹射实验台Fig.1 Test bench of rail ejection

轨道弹射实验台实物如图1所示，其结构示意图如图2所示，实验台主要由导轨、模拟列车(由滑块、弹簧和车轮组成)、钢轨、弹射装置和基座组成。实验台又可以分为弹射段、检测段和减速段。检测段钢轨长度为1100 mm，包含两跨，每跨长度为550 mm。实验台的钢轨的横截面为矩形，矩形的高为28 mm，宽为14 mm。轨道弹射实验台的详细结构可参考文献［8］。实验台上方安装有导轨，模拟列车可以在导轨上滑动，模拟列车通过弹簧将1个车轮压在钢轨上。本研究中使用的弹簧刚度为10 N/mm。

图2 轨道弹射实验台结构示意图Fig.2 Structure chart of rail ejection test bench

1.2 轨道实验台有限元模型

本文主要对轨道弹射实验台的检测段进行研究，钢轨检测段由两跨组成。运用非线性有限元分析软件ABAQUS建立轨道实验台检测段的三维轮轨接触有限元模型。有限元模型如图3所示。有限元模型中车轮与滑块通过1个刚度为10 N的弹簧单元联接，弹簧的压缩量为30 mm。本有限元模型用弹簧单元模拟实验台的支撑。有限元模型的各部件采用一阶六面体减缩积分单元C3D8R进行离散，钢轨的网格单元格的边长为4 mm。各部件的材料属性设置为钢。钢的材料属性如表1所示。

图3 三维轮轨接触有限元模型Fig.3 Finite element model of 3D wheel/rail

表1 钢材料属性参数Table 1 Material properties of steel

1.3 支撑的等效刚度

轨道弹射实验台的支撑结构如图4所示，钢轨通过螺栓固定在基座上，钢轨与基座间垫有橡胶垫块。为了提高运算速度，简化计算模型，本文有限元模型采用弹簧单元替代由橡胶垫块与螺栓构成的支撑。以如图4所示的轨道弹射实验台的支撑为物理原型，建立支撑的有限元模型，进行有限元分析，得到支撑的等效刚度。支撑的有限元模型中，钢轨、六角头螺栓和基座的材料属性设置为钢，其参数如表1所示。橡胶垫块的材料属性为超弹性材料，根据文献［9］，橡胶的材料模型使用Mooney－Rivlin模型［9］，橡胶的材料属性如表2所示。

表2 橡胶材料属性参数Table 2 Material properties of rubber

使用通用静态分析法［10］对支撑块有限元模型进行分析，共有4个分析步:第1个分析步，在螺栓上施加大小为250 N的预紧力，橡胶垫块产生0.241 mm的凹陷，与轨道弹射实验台上的橡胶垫块在预紧螺栓后产生的凹陷值相等;第2个分析步，将预紧力的施加方法改为固定螺栓的长度，更接近螺栓预紧的实际情况;第3个分析步，在钢轨上表面施加1个Fv=300 N的平均分布力，提取上表面沿作用力方向的平均位移 Wv=3.64×10－3mm。支撑的等效刚度 Kv=Fv/Wv=8.25×107N/m;第4个分析步，在钢轨横截面上施加1个Fh=300 N的平均分布力，提取横截面沿作用力方向的平均位移Wh=3.29×10－2mm。支撑的等效刚度 Kh=Fh/Wh=9.13×106N/m。

图4 支撑结构图Fig.4 Structure chart of rail support

本文模型由2跨轨道组成，共有3处支撑。轨道两端支撑为中部支撑的1/2，故轨道两端支撑的水平刚度与竖直刚度为中部支撑的1/2。为近似模拟实际支撑，本模型在每个支撑位置各添加2列水平方向与竖直方向的弹簧单元，每列平均分布3个弹簧单元，中部的支撑弹簧的竖直方向的总刚度为8.25×107N/m，水平方向的总刚度为9.13×106N/m。钢轨两端支撑弹簧的竖直方向的总刚度为4.13×107N/m，水平方向的总刚度为4.57 ×106N/m。

2 有限元计算结果及其分析

本文主要分析钢轨在动载荷作用下的动应力响应。在有限元分析中设定小车以11 m/s的速度通过钢轨，耗时 0.1 s。

本文采用如图3所示的坐标系，坐标系的X方向与钢轨的横截面垂直。定义S11，S22和S33分别为X方向正应力、Y方向正应力、Z方向正应力。图5～8所示为车轮经过钢轨的跨中时3个方向正应力及Mises等效应力分布云图。由图5～8可知:钢轨在车轮移动载荷作用下，S11应力响应最大，其最大值为13.97 MPa。S22与S33应力响应较小，最大值分别为0.21 MPa 和0.37 MPa。

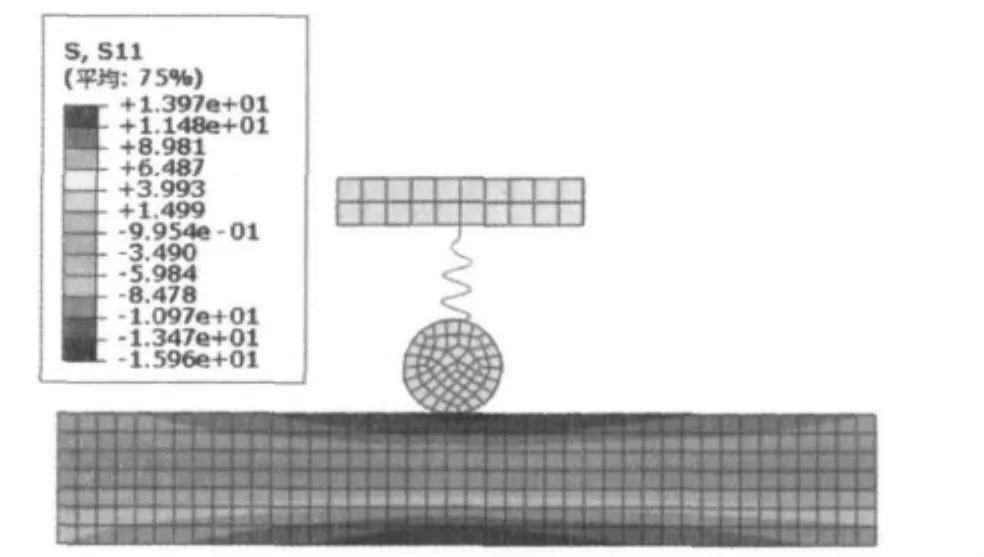
图5 车轮经过跨中时局部钢轨的S11应力分布Fig.5 Distribution of S11 at the rail passes middle－span

图6 车轮经过跨中时局部钢轨的S22应力分布Fig.6 Distribution of S22 at the rail passes middle－span

图7 车轮经过跨中时局部钢轨的S33应力分布Fig.7 Distribution of S33 at the rail passes middle－span

图8 车轮经过跨中时局部钢轨的Mises应力分布Fig.8 Distribution of Mises when the rail passes middle－span

图9所示为钢轨侧面上坐标为X=276 mm，Y=－10 mm的节点3个方向的正应力随时间变化规律。综合图5～9可知:钢轨在沿钢轨方向的正应力S11的应力响应远大于其他2个正应力方向的响应。故本文主要分析应力S11。

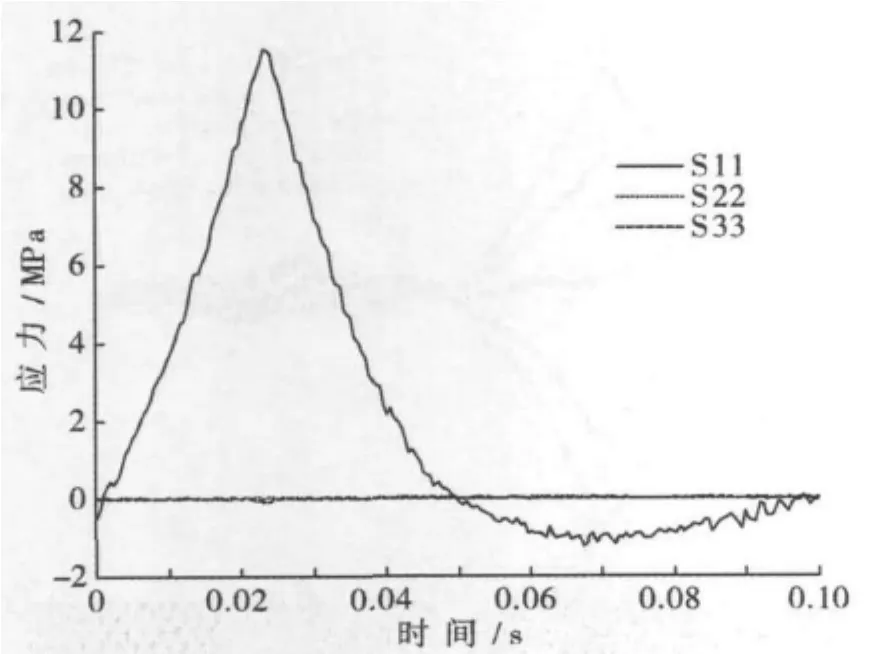
图9 节点(X=276 mm，Y=－10 mm)正应力变化Fig.9 Normal stress variation on a node(X=276 mm，Y= －10 mm)

为研究S11应力在Y方向上的分布规律，在X=276处选取Y坐标为－14～+14间的8个节点，在图10中绘出这8个节点的S11应力随时间的变化规律。从图10可知:应力在Y方向上近似关于Y=0反对称分布，且在Y的正方向上应力响应的绝对值略大于对称位置的应力响应。

图10 X=276 mm处8节点S11应力变化规律Fig.10 S11 stress variation on 8 nodes at X=276 mm

为研究应力响应在X方向的分布规律，在钢轨侧面上y=－10处建立一条起点为X=0，终点X=1100的路径，命名为路径Ⅰ。在路径Ⅰ上选取X坐标为124～424 mm之间的5个节点绘出S11应力的变化规律。图11所示为这5个节点S11应力随时间的变化规律。从图11可知:当车轮向节点驶近时，节点的应力响应增大，当车轮驶离节点时，节点的应力响应减小，且在X=276 mm处的应力响应最大;在X轴方向上，距离跨中位置的距离越远，其最大动力响应越小。

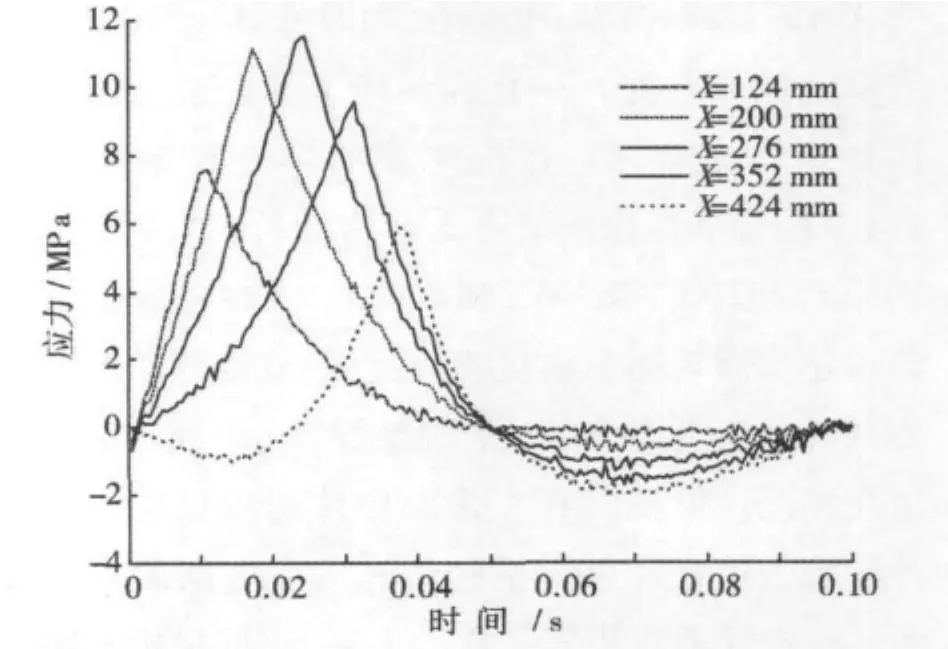
图11 多节点S11应力变化规律Fig.11 S11 stress variation on mult－ nodes

图12所示为路径Ⅰ的S11应力值随时间和X坐标变化规律的三维曲面图。由图12可知:当车轮经过钢轨时，路径Ⅰ上的应力响应存在2个波峰。波峰在钢轨的跨中位置，最大应力为11.62 MPa。综合以上分析可知最大应力响应点的坐标为X=276 mm，Y=14 mm，即在钢轨的跨中最上方。

图12 动应力响应变化Fig.12 Dynamic response variation

3 实验验证及其分析

为验证有限元分析的结果，本研究通过在钢轨上粘贴应变片，获得轨道实验台检测段钢轨的应力数据，应变片的粘贴位置如图2所示。应变片的粘贴方向垂直于钢轨横截面，用以检测S11应力。由于应变片需要占用一定的空间，有限元分析得到的应力响应最大的点(X=276 mm，Y=14 mm)在轨道的边缘，没有粘贴空间。本实验选定一个靠近应力响应最大点的位置粘贴应变片，具体的坐标位置为X=276 mm，Y=10 mm。同时在 X=276 mm，Y方向坐标分别为6，－6和－10 mm处也粘贴3片应变片作为对比。在检测段的第一跨钢轨侧面Y=－10 mm处也安装有5片应变片，其X坐标分别为124，200，276，352 和424 mm。在文献［3］中，轨道超偏载传感器由应变片组成，应变片的粘贴位置的X坐标为115 mm，Y轴坐标为－4 mm，本实验也在相同位置粘贴有1片应变片用以对比。应变片输出的信号经过电桥和信号放大电路放大。放大后的电压通过数据采集卡采集，数据采集的频率为10 kHz。

当模拟列车以10.1 m/s的速度通过检测段时，在钢轨侧面Y=－10 mm处安装的5片应变片输出信号经放大电路放大后输出电压如图13所示。由图13可知，在X=276 mm处的应力响应最大。采集到的电压信号与有限元分析结果相符。在X=276 mm处与X=115 mm处粘贴的应变片输出信号经放大电路放大后输出电压如图13所示。由图13可知，在相同的信号放大电路与相同的放大倍数下，在X=115 mm，Y=－4 mm处的动应力响应远小于最大应力响应点附近的动应力响应，将应力传感器安装在最大应力响应点附近，采集到的有效信号显著提高，在噪声信号近似不变的情况下，信号的信噪比显著提高。同理，将基于应力检测法的超偏载检测传感器安装在最大应力响应点附近可显著提高信号的信噪比。

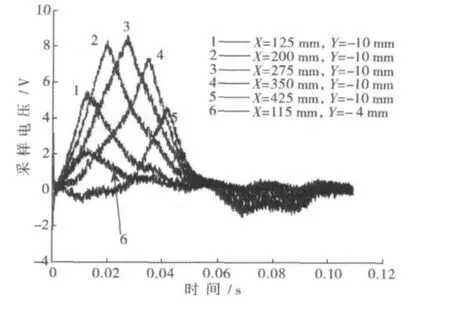
图13 Y=－10 mm处与X=115 mm处应变片信号对比Fig.13 Comparison of strain gauge signal between Y=－10 mm and X=115 mm

图14 X=256 mm处与X=115 mm处应变片信号对比Fig.14 Comparison of strain gauge signal between X=256 mm and X=115 mm

4 结论

(1)钢轨在车轮动载荷作用下，最大的正应力方向垂直于钢轨的横截面。

(2)钢轨的最大动应力响应点在钢轨跨中最上方。

(3)将超偏载检测传感器安装在最大应力响应点附近可显著提高信号的信噪比。

［1］韩自力，张千里.既有线提速路基动应力分析［J］.中国铁道科学，2005，26(5):1 －5.HAN Zi1i，ZHANG Qian1i.Dynamic stress analysis on speed－increase subgrade of existing railway［J］.China Railway Science，2005，26(5):1－5.

［2］贺建清，曾京.轻便型铁路货车超偏载检测装置［J］.中国铁道科学，2010，31(6):137 －140.HE Jianqing，ZENG Jing.A portable type of device for detecting the overload and unbalanced load of railway freight car［J］.China Railway Science，2010，31(6):137－140.

［3］刘超.高速扫掠力轨基检测系统集成研究［D］.长沙:中南大学，2010.LIU Chao.Research of integrated monitor system in high speed sweeping force rail［D］.Changsha:Central South University，2010.

［4］黄志辉，赵红伟.钢轨应变分布场的有限元分析［J］.机电工程，2007，24(4):13－15.HUANG Zhihui，ZHAO Hongwei.Finite element analysis of rail strain distribution［J］.Mechanical＆ ElectricalEngineering Magazine，2007，24(4):13－15.

［5］Mazilu T.Green’s functions for analysis of dynamic response of wheel/rail to vertical excitation［J］.Journal of Sound and Vibration 306(2007)31－58.

［6］黄志辉，陈庆广，李屹罡，等.移动质量速度对钢轨动力响应的影响［J］.铁道科学与工程学报，2012，9(1):122－124.HUANG Zhihui，CHEN Qingguang，LI Yigang，et al.The effect of moving mass velocity on the dynamic response of the rail［J］.Journal of Railway Science and Engineering，2012，9(1):122 －124.

［7］马劲红，陈伟，张文志.波纹轨腰钢轨万能轧制数值模拟与实验研究［J］.塑性工程学报，2009，16(1):120－124.MA Jinhong，CHEN Wei，ZHANG Wenzhi.Numerical simulation and experimental study on corrugated waist rail with universal rolling［J］.Journal of Plasticity Engineering，2009，16(1):120 －124.

［8］杨海军.列车车轮扫掠力检测实验台的设计与研究［D］.长沙:中南大学，2008.YANG Haijun.Design and research of rail sweeping force test bench［D］.Changsha:Central South University，2008.

［9］陈盛钊，高速扫掠力作用下轨基检测位置动力响应分析与实验研究［D］.长沙:中南大学，2011.CHEN Shengzhao，Experiment and analysis of rail dynamic response under high speed sweeping force［D］.Changsha:Central South University，2011.

［10］石亦平，周玉蓉.ABAQUS有限元实例详解［M］.北京:机械工业出版社，2011.SHI Yiping，ZHOU Yurong.Example explanation of ABAQUS［M］.Beijing:China Machine Press，2011.