汽车车桥结构的有限元分析

刘 昕

(西安汽车职业大学，陕西 西安 710600)

0 前言

作为汽车的承载模块，车桥是整车结构的关键部件之一，其动态特性对汽车整体性能具有直接的影响。有限元分析广泛应用于各种线性和非线性问题，是一种分析大型复杂工程结构的有效方法。随着计算机技术的发展，有限元分析已成为结构分析的常用方法，可以实现多种几何形状、边界条件的结构分析和优化[1]。因此，采用有限元分析探究汽车车桥的结构特性具有现实意义。

1 汽车车桥结构有限元分析

1.1 车桥结构参数的导入

本文以某品牌越野车为例进行车桥结构有限元分析。该越野车搭载了前置发动机，采用四轮四驱方式，核定乘员为4人，最高车速大于120 km/h。前后悬架均采用空气弹簧式悬架，整车采用齿轮齿条式转向系统，制动系统采用钳盘式制动器。整车电气系统和液压系统均采用统一设计布置，系统的一体化程度较高。该越野车的其他技术参数为：轴距3 800 mm，轮距1 680 mm，整备质量3 800 kg，额定总质量5 800 kg，前桥最大轴荷2 000 kg，后桥最大轴荷3 800 kg。

1.2 有限元建模

MSC.Patran软件是一款有限元分析求解器，具有工程分析、干涉报警、用户自定义、结果评估等功能，可以实现从产品设计到生产制造整个流程的性能仿真[2]。采用MSC.Patran软件对某品牌越野车的车桥结构进行了建模和有限元网格划分。

该车桥结构的有限元分析实体包括4个点约束和4个面约束。其中，每个点约束包括3个平移自由度约束和1个旋转自由度约束[3]。为了准确表达实体部件信息，可从空间视角着手，仅考虑3个平移自由度，进行实体几何形状的真实逼近，获得反映汽车车桥结构全部几何变换的有限元模型。

经过有限元网格划分后的汽车车桥结构模型如图1所示。通过有限元网格计算，该车桥结构内节点数量为10 951个，单元体数量为6 352个，网格划分密度较高的位置处于车桥变截面区域。

图1 车桥结构的有限元网格模型

1.3 材料配置

在建模过程中，忽略了汽车车桥安装缝隙、进油孔和倒角等细部结构，仅根据车桥组件部位差异进行不同材料的配置[4]。该汽车车桥结构主要部件的材料性能参数如表1所示。

表1 汽车车桥结构主要部件的材料性能参数

2 静力学分析

2.1 最大制动力工况

在车辆满载并处于紧急制动的工况下，不考虑侧向力的影响，汽车车轮不仅要承受来自地面的制动应力，还要承受垂直载荷应力。其中，最大地面制动应力为车辆在满载时相对于车辆在水平路面静止时车桥施加的载荷应力。通过该车辆的实际行驶工况试验测得，该数值为990.0 MPa[5]。由于车辆满载并处于紧急制动工况下，其最大制动力可转化为施加在后轮空气弹簧座外侧的2 个垂直力和施加在轮毂内轴上的扭矩，可设定约束条件为：车桥端面位置节点的X轴方向平移、Y轴方向平移和Z轴方向平移，以及沿Y轴方向的旋转。

在车轮与地面附着系数为0.7的情况下，在紧急制动工况下车轮处于滑动状态，车桥结构承受的制动力为最高水平，测得最大制动力为3 480.0 N。通过经验公式测算，由最大制动力引起的扭矩为最大制动力与扭矩系数(系数为0.66)的乘积，该扭矩为2 241.6 N·m。在最大制动力工况下，运用MSC.Patran软件对汽车车桥关键位置的应力值进行了计算，计算结果见表2。

表2 最大制动力工况下车桥关键位置的应力值

由表2可知，该车辆在最大制动力工况下，车桥的最大应力值为70.0 MPa，位于车桥头部，小于材料的屈服强度极限和抗拉伸强度极限，满足车桥结构的可靠性要求。

2.2 最大驱动力工况

在行驶路面比较平坦，车辆处于满载且驱动力最大的工况条件下，此时汽车车桥结构主要受到车身载荷、对应轮胎的反作用力及车桥切向力的作用，且均处于最大值。在不考虑侧向力和特殊路面条件的情况下，由传动轴作用产生的切向力是威胁车桥结构可靠性的主要因素。汽车车桥单侧承受扭矩L的计算公式为：

式中，Lmax为传动输出轴的扭矩最大值，单位N·m；i为减速比；n为传动效率。

通过计算可得，车桥单侧承受扭矩L为217.2 N·m。在约束车桥边界条件下，将该扭矩和载荷力分别施加到弹簧座两端后，可得出在最大驱动力工况下汽车车桥承受的应力值，见表3。

表3 最大驱动力工况下车桥关键位置的应力值

由表3可知，车辆在最大驱动力工况下，车桥关键位置的应力最大值为214.5 MPa，位于空气弹簧底座靠近车桥头部(即半轴壳管与板簧座连接位置)，其最大应力值小于材料屈服强度极限，满足车辆在最大驱动力工况下行驶时的车桥稳定性要求。

2.3 最大侧向力工况

在汽车满载且发生侧滑的情况下，车辆全部载荷的承受对象可认定为发生侧滑的车轮。车桥承受的侧向力为汽车满载且相对于水平路面静止时车辆给予地面的载荷与轮胎路面侧向附着系数的乘积[6]。因最大侧向力可转化为侧滑方向一侧的施加力，可分解为水平方向的侧向力、施加在Z轴上的扭矩，以及车辆另一侧的垂直力。约束条件可设定为：车桥抗滑端面X轴方向的平移、Z轴方向的平移和Y轴方向的旋转，以及另一端面的X轴方向平移、Y轴方向平移和Z轴方向平移。运用MSC.Patran软件，对多载荷作用下汽车车桥关键位置的应力值进行了计算，计算结果见表4。

由表4可知，车辆在最大侧向力工况下，车桥最大应力约为70.0 MPa，位于车桥结构的两端，主要是由于车辆在高速、满载，并处于侧滑的极限工况下，与侧滑方向不同的车轮垂直反向力和侧向力几乎为零，而与侧滑方向一致的车轮垂直反向力和侧向力则达到最大值，车桥尾部(轮毂轴承侧)所承受的应力最大。该最大应力值小于材料屈服强度极限，可以保证车辆在最大侧向力工况下的车桥结构稳定性。

表4 最大侧向力工况的车桥关键位置的应力值

2.4 最大垂直力工况

在汽车满载且行驶路面不平整的情况下，汽车所承受的载荷为冲击载荷，可以忽略侧向力和切向力的作用，将车桥壳体简化为简支梁。设定冲击载荷为2.5倍满载荷载，载荷承受部位为空气弹簧座，施加在左侧弹簧座上的载荷G左和施加在右侧弹簧座上的载荷G右的表达式分别为：

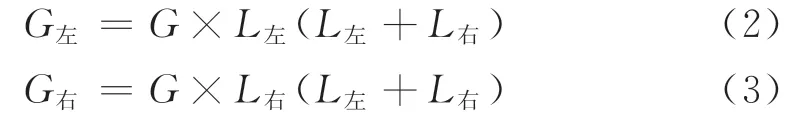
式中，L左、L右分别为左侧和右侧空气弹簧座中心与车桥中心位置的距离，单位mm。

最大垂直力可视为均等施加在空气弹簧座各节点上的载荷力，设定约束条件为：汽车车桥一端端面节点的X轴方向的平移、Y轴方向的平移和Z方向的平移，以及车桥另一端面节点的X轴方向的平移、Y轴方向的旋转和Z轴方向的平移。根据该车辆满载设计质量为9.9 t，运用MSC.Patran软件，对最大垂直力工况下的汽车车桥关键位置的应力值和变形量进行了计算，计算结果见表5。

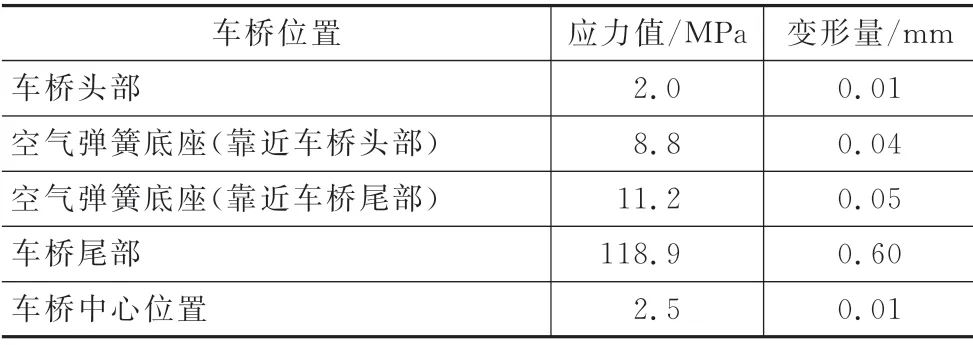
表5 最大垂直力工况下车桥关键位置的应力值和变形量

由表5可知，在最大垂直力工况下，车桥关键位置的最大应力值为118.9 MPa，位于车桥一端，处于材料屈服强度极限内，能够满足车桥的安全性需求。此外，根据国家对汽车车桥结构的可靠性要求，在车辆承受最大垂直载荷时，最大变形量应小于1.5 mm。因此，该车辆的车桥结构满足最大垂直力工况下的强度和刚度需求。

考虑到汽车车桥一端承受的应力值远远高于另一端，为了避免汽车在最大垂直力工况下发生车桥端断裂，可以在保证汽车车桥外壳受力位置一定的情况下增加车桥外壳厚度，提高车桥的刚度。一般而言，当汽车车桥厚度为3.5 mm 时，车桥端承受的应力处于最大值，随着车桥厚度的增加，其所承受的应力也会下降，最佳的车桥厚度为4.3 mm。

3 结语

综上所述，利用有限元分析，可以将具有多个自由度的汽车弹性连续体转化为仅有若干自由度的单元集合体，通过数值解法可简化边界条件复杂的大型连续载荷，为车桥结构的优化提供数据支撑。本文利用计算机软件建立汽车车桥结构的有限元模型。在有限元模型内，通过分析最大垂直力、最大驱动力、最大制动力及最大侧向力，计算汽车车桥结构承受的应力。同时，根据汽车车桥结构承受应力的情况，优化车桥结构，解决车桥结构因应力集中而导致的可靠性下降问题，提高车辆行驶的安全性和稳定性。