聚合物驱数学模型的建立

宋洪才，张 儒

(东北石油大学数学科学与技术学院，黑龙江大庆 163318)

根据聚合物驱油机理及实际情况研究，在实际油藏中，从注入井到采出井，聚合物溶液浓度是逐渐减小的，但其在地层中的分布规律尚无人给出一种简单适用的表达式。为了研究聚合物驱油后各组分的变化规律，本文通过对基本聚合物驱油的数值模拟研究，来进一步讨论聚合物溶液分布规律［1－2］。

1 聚合物驱的主要数学模型

聚合物驱模型是基于Np相、Nc组分可压缩带吸附混溶和非混溶混合驱动的数学模型。它的基本方程如下。

1.1 物质守恒方程

在考虑黏性力、重力、毛管力和物理弥散条件下，多组分化学渗流方程为:

这里k表示组分号，Nc为组分数;Wk为组分k的质量浓度，Fk为达西速度和物理弥散项，Rk为源汇项。

1.2 压力方程

将上述组分物质方程叠加，代入相应的达西速度项和源汇项，可得到以压力P为未知函数的方程式为:

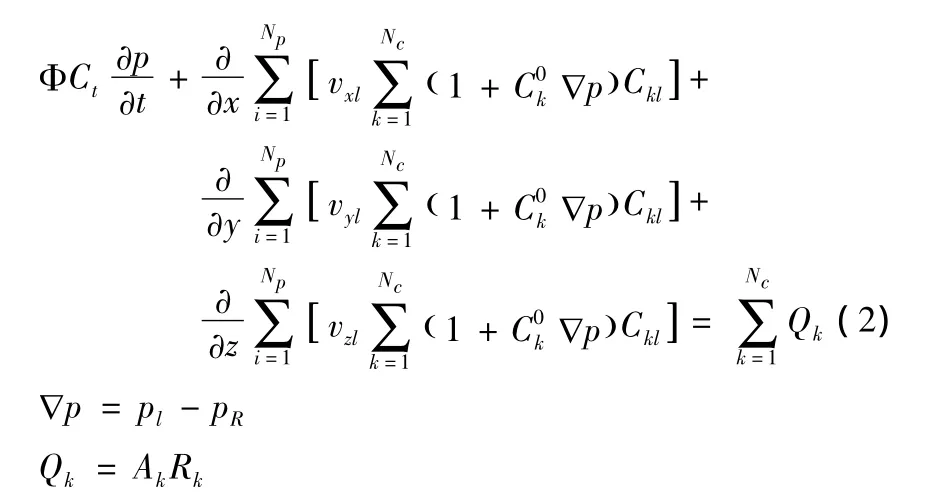
式中:Ckl－l相中组分k的浓度;vDt－l相中D方向上达西速度分量，D=x、y、z;Np－相数;Ct－综合弹性系数;pl－l相压力;pR－参考(基准)压力;Ak－换算系数。

1.3 浓度方程

从物质守恒方程出发可得到关于浓度方程式:

式中:Ck－组分k的浓度;WDi－弥散系数，D=x、y、z，i=1、2、3［3］。

2 聚合物驱溶液变化的主要数学模型

目前，国内外所有的聚合物驱油数学模型都是基于HPAM的溶液性质特点建立起来的，在近年来聚合物溶液结构研究成果的基础上，通过试验，总结出聚合物溶液的结构特点和结构变化规律，以及结构在宏观动态上的表现规律。提出采用线形体和聚集体共同描述聚合物溶液驱油动态，从而建立适合聚驱后溶液变化的数学模型［4］。

2.1 基本渗流方程

聚合物驱模型是一个三相五(拟)组分模型，五组分分别为油、气、水、聚合物线形体及聚合物聚集体。基本渗流方程由达西定律与物质守恒定律控制，包括了流动项、源汇项以及累积项。单相的连续方程微分形式是:

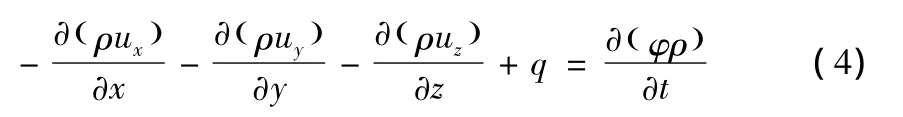
式中:ρ－流体密度;uD－方向体积流速，D=x、y、z;q－质量流速;φ－孔隙度。

2.2 油组分渗流方程

应用多相渗流的达西方程，可以将油相的地下体积流速表示为:

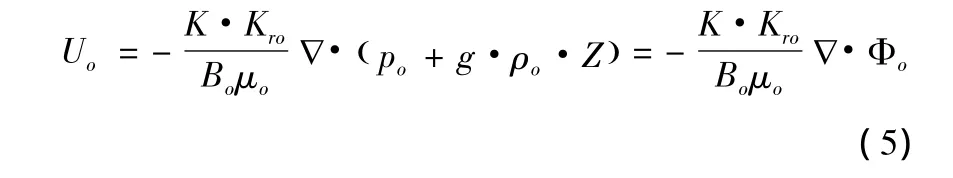
多相渗流的油组分连续方程为:

将式(5)代入式(6)，就可以得到多相渗流的油组分渗流方程:

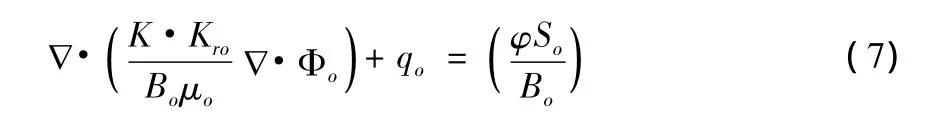
式中:Uo－油相体积流速;Φo－油相的压能及位能，称为势能函数;K－多孔介质渗透率;Kro－油相相对渗透率;Bo－油相体积系数;μo－油相黏度;So－含油饱和度。

2.3 气组分渗流方程

同样的道理，气相的地下体积流速表示为:

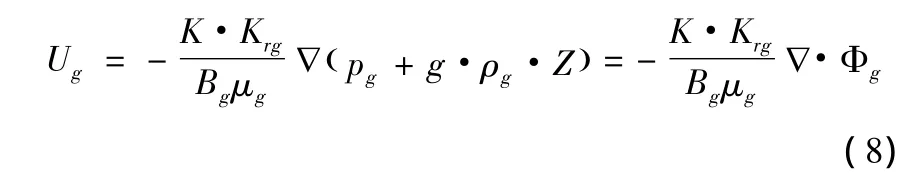
由于气组分存在于油相和气相中，气组分的连续方程就与油相和气相有关了，表示为:

将式(5)和式(8)代入式(9)中，得到气组分的渗流方程:

式中:Ug－气相体积流速;Φg－气相的压能及位能;Krg－气相相对渗透率;Bg－气相体积系数;μg－气相黏度;Sg－含气饱和度;Rs－溶解油气比。

2.4 水组分渗流方程

水相的地下体积流速表示为:

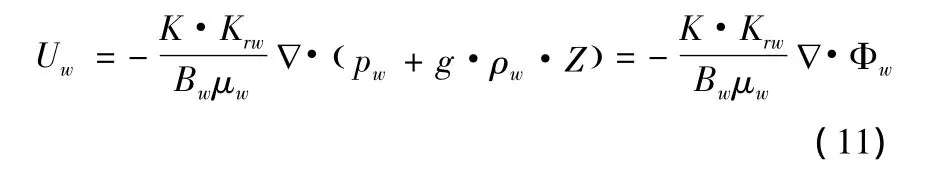
水相连续方程为:

水相渗流方程为:

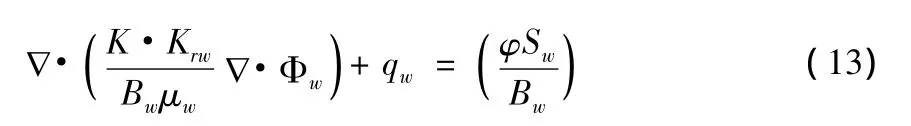
由于水相中包括了水组分、聚合物线形体组分和聚合物聚集体组分，假设各组分在水相中的浓度分别是Cww、Cwp和Cwg则水组分的渗流方程为:

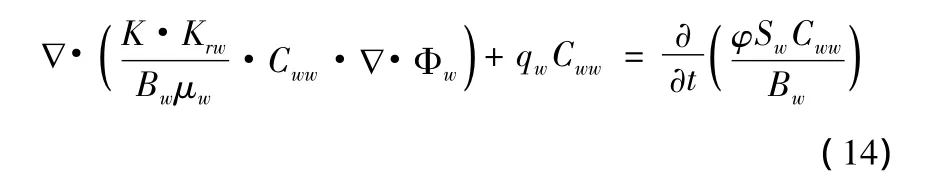
式中:Uw－水相体积流速;Φw－水相的压能及位能;Krw－水相相对渗透率;Bw－水相体积系数;μw－水相黏度;Sw－含水饱和度;Cww－水相中水组分浓度。

2.5 聚合物线形体组分渗流方程

聚合物线形体组分只存在于水相中，渗流方程与水组分渗流方程类似。

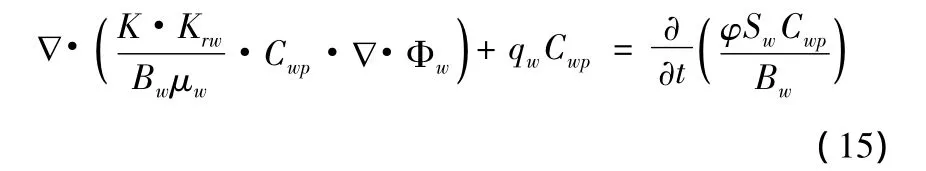
考虑到吸附作用，渗流方程可为:

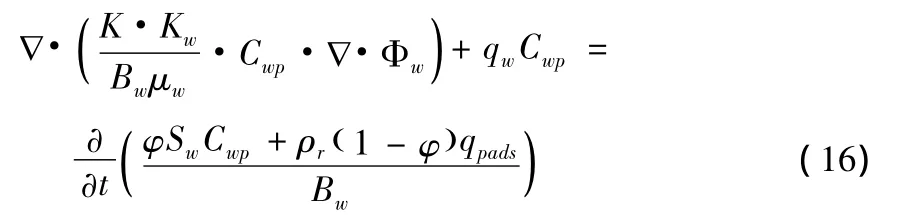
考虑到扩散弥散作用，扩散弥散作用符合Fick定律，弥散速度张量为:

渗流方程为:

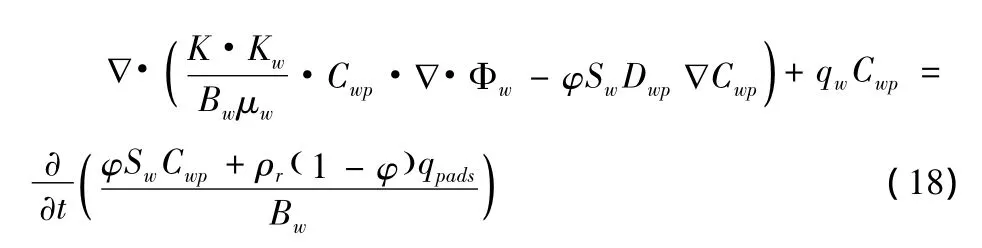
最后考虑到聚合物线形体组分向聚合物聚集体组分的转化，其渗流方程为:

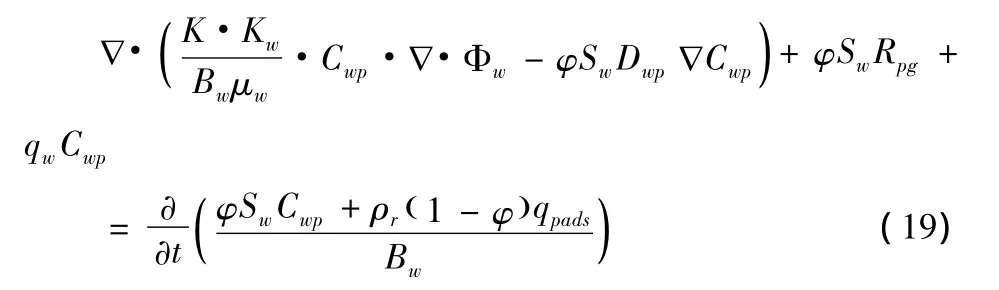
式中:Cwp－水相中聚合物线形体组分浓度;ρr－岩石密度;qpads－聚合物线形体在岩石上的吸附量。Dwp－聚合物线形体弥散系数Rpg－聚合物线形体向聚合物聚集体转化速度。

2.6 聚集体组分渗流方程

聚合物聚集体组分也只存在于水相中，渗流方程为:

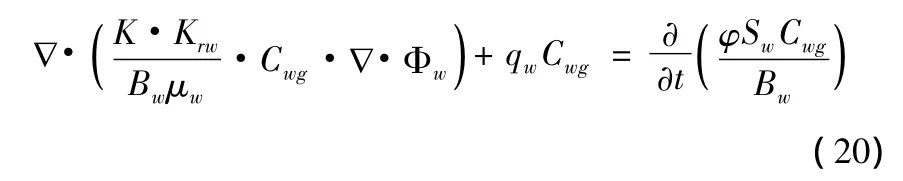
考虑到聚合物聚集体组分的扩散弥散作用、岩石的吸附作用和向聚合物线形体组分的转化，渗流方程为:

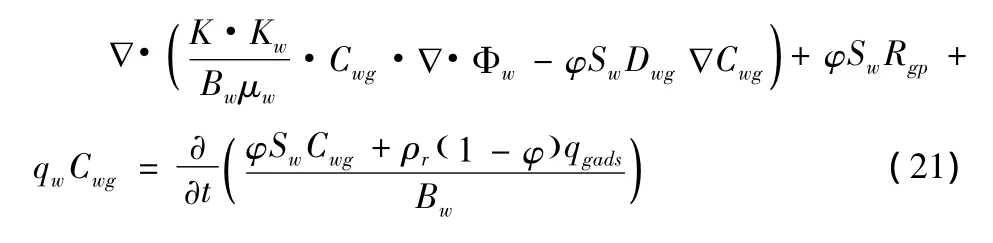
式中:Cwg－水相中聚合物聚集体组分浓度;Dwg－聚合物聚集体弥散系数;Rgp－聚合物聚集体向聚合物线形体转化速度;qgads－聚合物聚集体在岩石上的吸附量［5］。

3 结论

(1)在聚合物驱数值模拟的主要数学模型的基础上研究聚驱后各组分变化的渗流方程及模型。

(2)在一般聚合物驱油模型的基础上，考虑了不同孔渗条件下水相相对渗透率降低能力、不可及孔隙体积系数的变化、吸附滞留与建立流动阻力的关系等物化问题，能够更好地描述聚合物溶液与地层岩石的相互作用。

(3)所建立的聚合物驱模型可用于常规聚合物驱模拟和动态预测，可为聚合物驱后深入研究提供理论指导。

［1］王新海，韩大匡，郭尚平.聚合物驱油机理和应用［J］.石油学报，1994，15(l):85 －86.

［2］杨二龙.聚合物驱试井解释方法研究［D］.大庆:大庆石油学院，2002.

［3］戚连庆.聚合物驱油工程数值模拟研究［M］.北京:石油工业出版社，1998:2－3.

［4］陈国，赵刚，马远乐.聚合物交联调剖驱油数学模型［J］.清华大学学报(自然科学版)，2004，44(12):1606 －1609.

［5］叶仲斌，洪楚侨，施雷庭，等.疏水缔合聚合物驱油数学模型［J］.西南石油大学学报，2007，(12):172－173.