对圆锥曲线定点弦三个性质的推广

☉

文［1］中给出圆锥曲线的三个性质，整理如下：

性质1：（文［1］性质12）与圆锥曲线焦点弦IJ所过焦点同侧的顶点是B，另一顶点是A.焦点弦端点I、J与A连线分别交相应准线于点M、N，则N、B、I三点共线，M、B、J三点共线（抛物线的另一顶点A在无穷远处）.

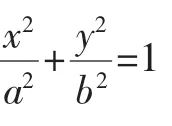
性质3：（文［1］性质17）椭圆的焦点弦所在直线被椭圆及短轴直线所分向量比之和为定值；双曲线的焦点弦所在直线被双曲线及虚轴直线所分向量比之和为定值；抛物线的焦点弦所在直线被抛物线及顶点处切线所分向量比之和为定值.

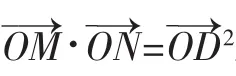
推广1.2：给定抛物线y2=2px及平行动弦EF，设动弦中点轨迹所在直线q（平行于x轴）交抛物线于D点，在直线q上取N、M两点（M在抛物线内），使DM=DN，过点N作与EF平行的直线l，过点M任意作直线交抛物线于A、B两点，作直线BC∥q交l于C，则A、D、C共线.

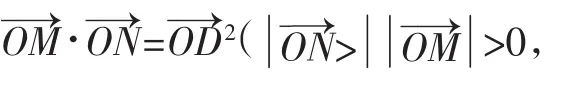
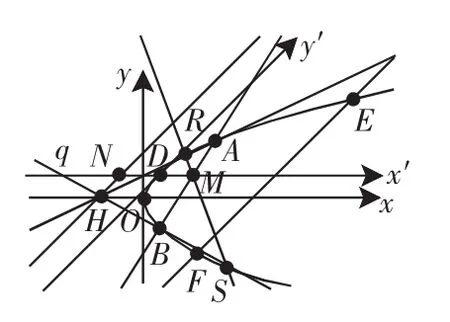
图1

推广2.2：如图1，给定y2=2px及平行动弦EF，设动弦中点轨迹所在直线q（平行于x轴）交抛物线于D点，在直线上q上取M、N两点（M在抛物线内）使DM=DN,过点M任意作两直线分别交椭圆（双曲线）于A、B；R、S点.延长AR、SB交于点H，则H点轨迹为过点N与EF平行的直线.

证明：设E（x1，y1），F（x2，y2），平行动弦EF所在直线方程为x=ky+d（k为定值，d为变量），与y2=2px（p＞0）联立，消去x，得y2-2pky-2pd=0.

以D点为新坐标原点，NM所在直线为x′轴，过D点与EF平行的直线为y′轴建立新坐标系.

在新坐标系中，设M（x0，0），N（-x0，0），A（xA，yA），B（xB，yB），

联立①、②得y′2-2p（k2+1）my′-2p（k2+1）x0=0，

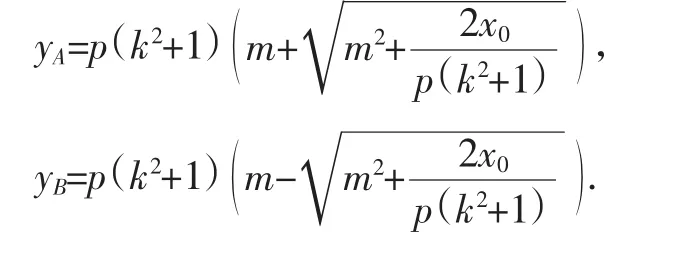
同理可设直线RS方程为x′=ty′+x0，得

即证H点轨迹为过点N与EF平行的直线.

推广1.1可由推广2.1导出：推广1.1中的弦DH、AB是过点M的两弦，由推广2.1，HB、AD延长线的交点在l上，又HB交l于点S，故S、D、A三点共线，同理R、D、B三点共线.

推广1.2可由推广2.2导出：推广1.2中的弦AB、射线DM是过点M的两弦（射线与抛物线另一交点在无穷远处），由推广2.1，AD延长线与B点和无穷远处连线（过B点平行于q的直线BC）的交点在l上，又BC交l于点C，故A、D、C三点共线.

推广2.1的证明与推广2.2类似，由于篇幅限制，此处略.

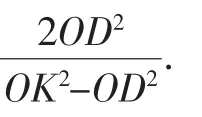
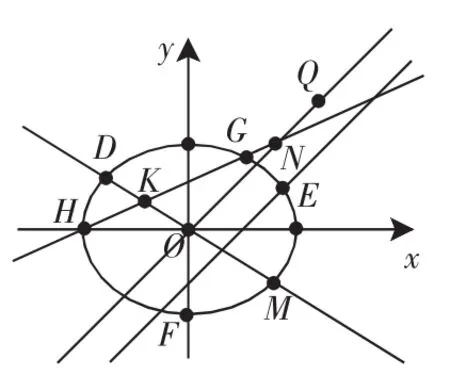
图2

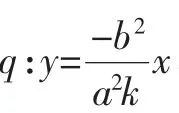
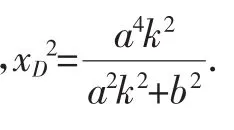
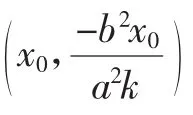
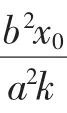
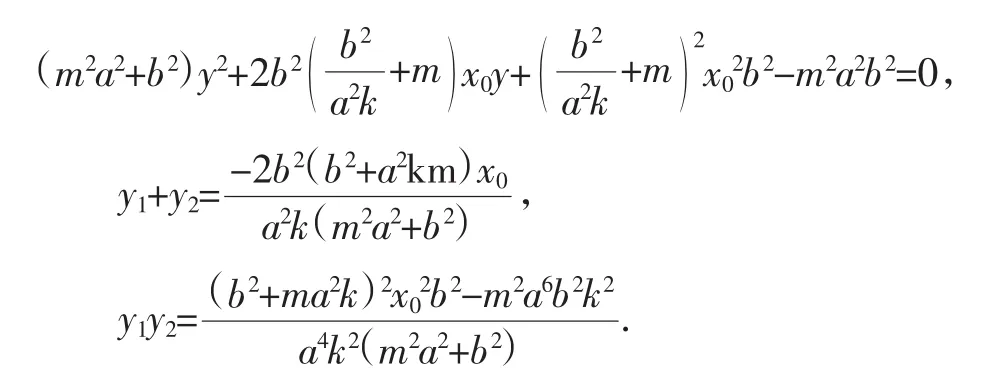
联立直线HN和直线OQ方程，得其交点

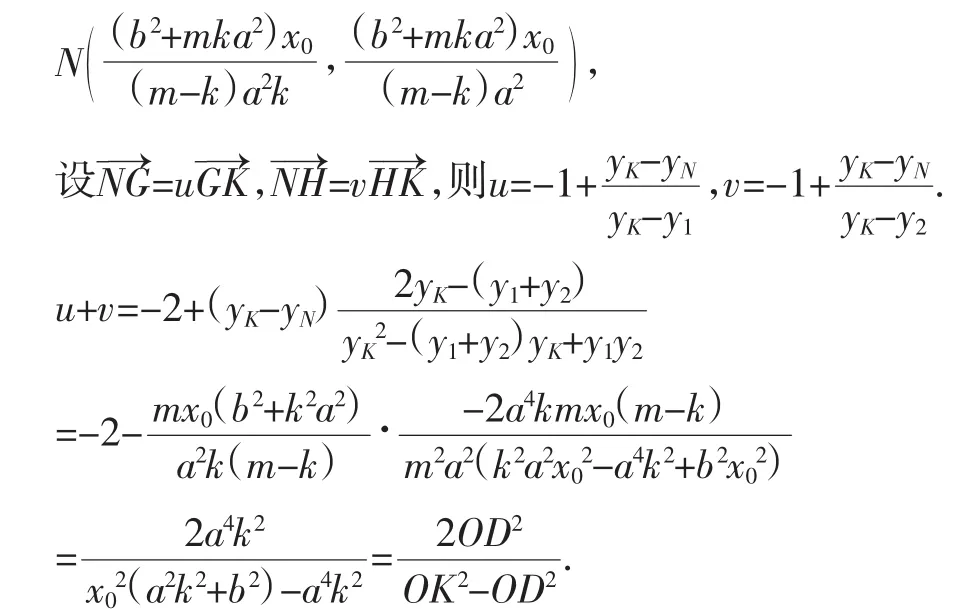
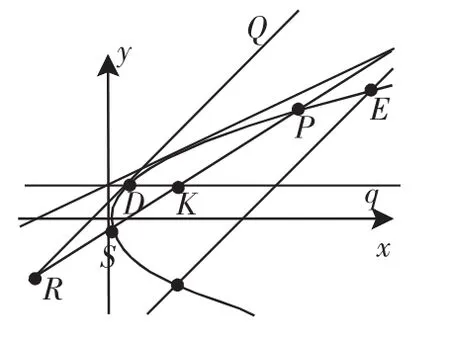
图3

推广3.2：如图3，给定抛物线及平行动弦EF，动弦中点轨迹所在直线q（平行于x轴）交抛物线于D点，记过D点平行于动弦EF的直线为DQ，过q上任一点K的弦所在直线被抛物线及直线DQ所分向量比之和为定值-1.

推广3.2的证明方法与推广3.1类似，本文不再给出.

结论

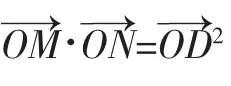
1.闻杰.圆锥曲线结构思想与解题策略［M］.杭州：浙江大学出版社，2010.

2.丁振年.对圆锥曲线两个性质的推广的再推广［J］.昭通师范高等专科学校学报，2003，5：18-20.