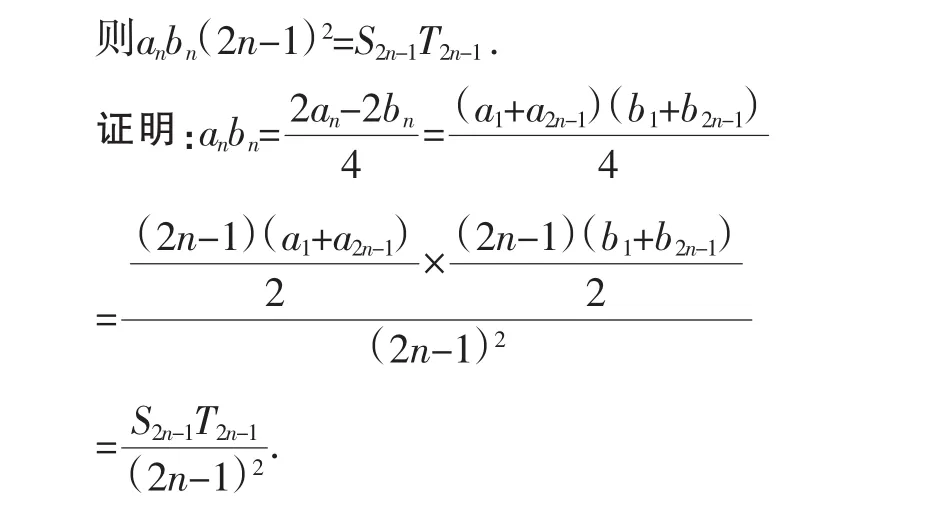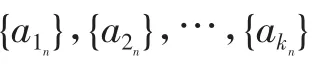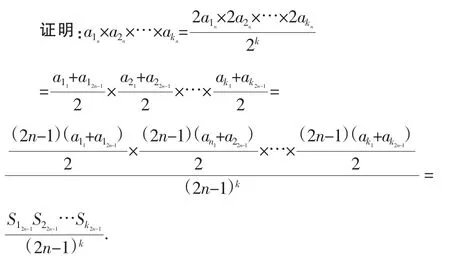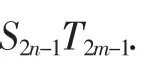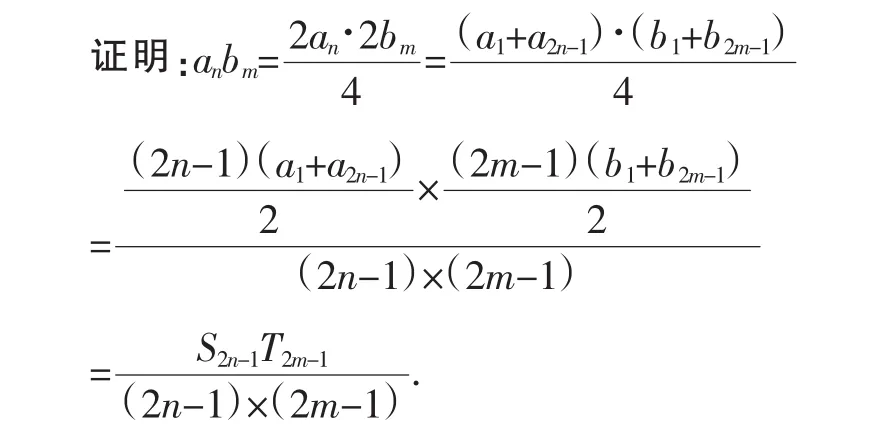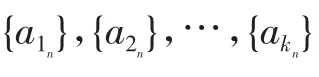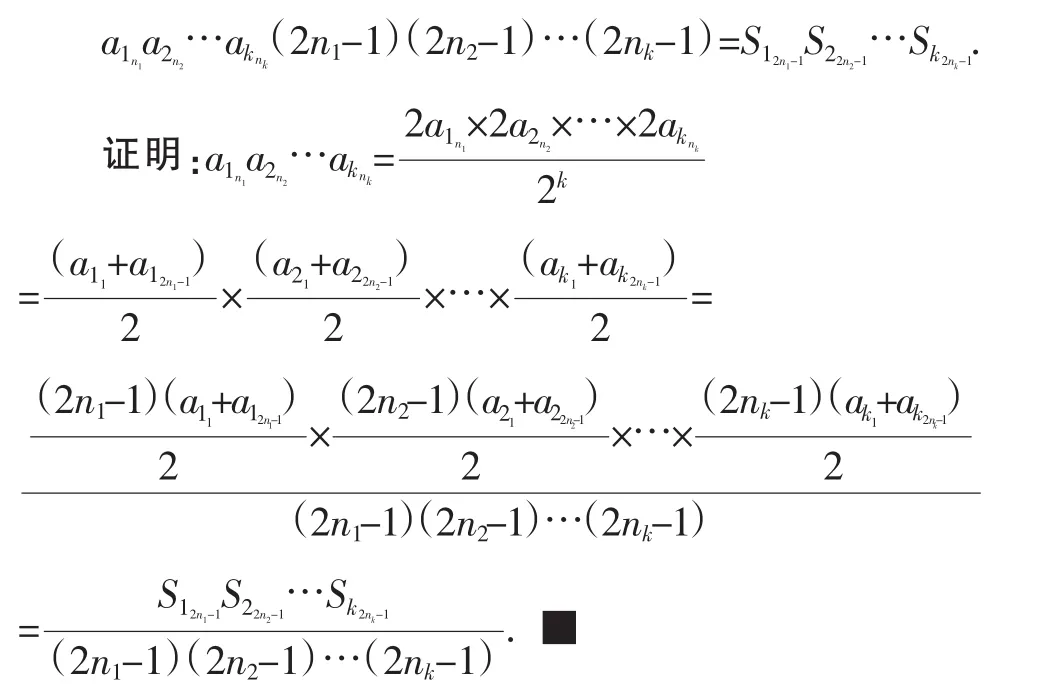对新教材课本习题的引申和研究
2013-07-25☉
中学数学杂志 2013年6期
☉
新课程的序幕已经拉开,教材的逻辑体系发生了变化,很多教师不太适应这样的教材,认为内容比较零散,但仔细研究教材以后,发现新教材和老教材没有什么本质的不同,新教材更能体现知识的螺旋式上升.欲更好的认识新教材,需要花一番功夫研究教材和习题,下面以笔者对一道经典习题的研究为例说明怎么样研究习题,并拓展.
人教A版全日制普通高级中学教科书第一册B组复习参考题:
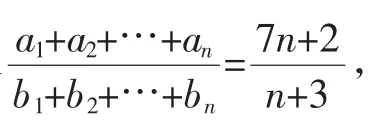
首先,抽象出题目的明确意思.
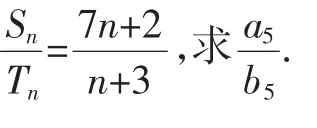
一、解题研究
解法1:联想求和公式2及通项公式
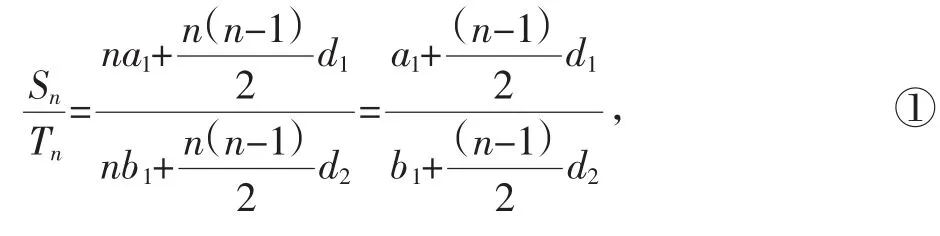
(a1,b1,d1,d2分别为an、bn的首项和公差)

解法2:联想求和公式1及等差中项的概念
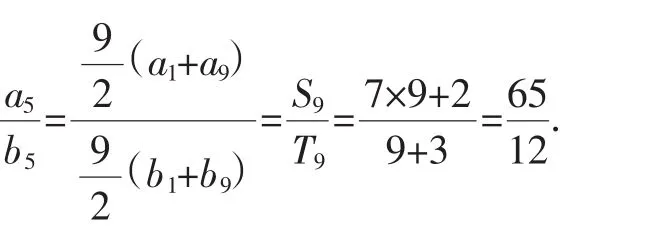
解法3:建立通项与和的比的一般关系(利用a1+a2n-1=2an)
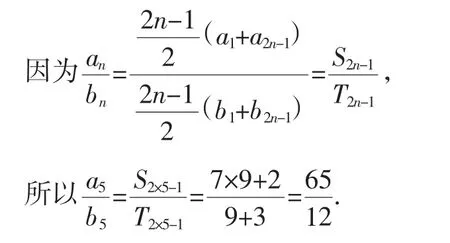
解法4:联想到数列{an}和{bn}是等差数列⇔Sn=an2+bn;
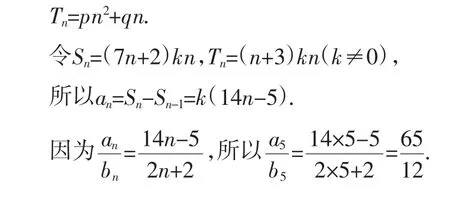
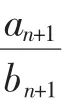
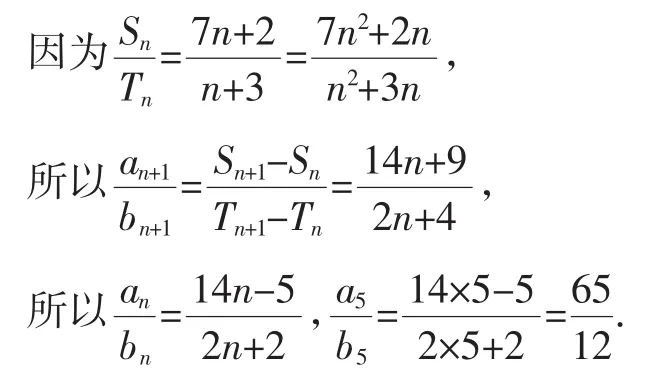
解法6:联想到平均数(等差中项),若an=m是{an}的前2n-1项的平均数,则S2n-1=(2n-1)m=(2n-1)an,
由此可见,探究多解法,可以开拓学生的思维.要充分发挥习题价值,当然还需要对它拓展研究.
二、题目再探
通过上述解法,不难发现,其核心问题是将两个等差数列和的比转化为通项的比,从而得到以下结论:
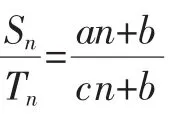
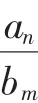
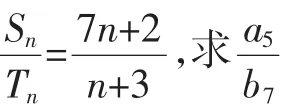
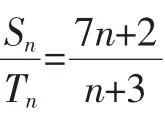
Sn=kn(7n+2),Tn=kn(n+3),于是
an=Sn-Sn-1=kn(7n+2)-k(n-1)[7(n-1)+2]
=k(14n-5);
bn=Tn-Tn-1=k(n+3)-k(n-1)(n-2)
=k(2n+2).
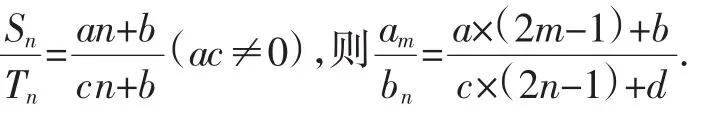
证明:

三、结论推广
既然两项的比与前n项和有联系,那么与它们的积有关系没有呢?
结论3:若两个等差数列{an}、{bn}的前n项和分别为Sn和Tn