让研究教材成为一种习惯——从教材对正弦定理证明的设置看新课标理念的变化

☉云南省大理第一中学 王永生

学校本学期开展同课异构教研活动，从而推动新课标理念在课堂教学中的落实.数学组选择的课题是人教社A版必修5第一章《解三角形》第一节《正弦定理》的第一课时.通过对教材的深入研究，结合对以前教材的认识，从教材对正弦定理证明的设置，可看出新课标理念有以下一些变化.

一、利用两个探究体现了新课标的特色

布鲁纳认为：探索是数学教学的生命线.倡导积极主动、勇于探索的学习方式，力求通过各种不同形式的自主学习和探究活动，让学生体验数学发现和创造的历程，这是高中《新课程标准》提出的重要理念之一.教材利用两个探究充分体现了这一理念.

第一个探究是“我们知道，在任意三角形中有大边对大角，小边对小角的边角关系，我们是否能得到这个边、角关系准确量化的表示呢？”.“问题是数学的心脏.有了问题，思维才有方向；有了问题，思维才有动力；有了问题，思维才有创新.”一个良好的数学问题情境，能集中学生的注意力，诱发学生思维的积极性，引起学生更多的联想，也比较容易调动起学生已有的知识、经验、感受和兴趣，从而更加自主参与知识的获取过程、问题的解决过程.现代建构主义学习观和教学设计理论都把问题解决作为建构性学习的基本策略.美国、澳大利亚等国对此问题也作了深入的研究，认为问题是思维的开始，问题解决过程就是思维发展过程，提出了抛锚式教学.可见，教材如此设置不仅为了彰显新课标的理念，而且符合现代教育教学的理论，更重要的是能促进学生自主学习，从而能较好地改变学生的学习方式.

第二个探究是“当△ABC是钝角三角形时，以上等式仍然成立吗？是否可以用其他方法证明正弦定理”.教材一改以往对证明的完整呈现，对学生力所能及的学习活动，以探究的形式进行设置，这是新教材最大的特点.其中第一个问题可在课内组织学生完成，让学生体验数学发现和创造的历程，而第二个问题可课内也可课外展开,从而使探究活动走向深入.

整个证明的设置从探究开始，以探究结束.一方面充分体现了新课标教材编写的特点，另一方面彰显了新课标“通过各种不同形式的自主学习和探究活动，让学生体验数学发现和创造历程”的理念.更重要的是使学生“养成了独立思考、积极探索的习惯”.

二、对证明方法的选择突出了对学生创新能力的培养

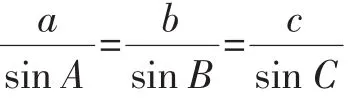
一是这种证法充分尊重学生初中已学知识，从学生的“最近发展区”入手进行设计，使新知识的形成显得较为自然，让学生很好地体验了数学“再创造”的过程，从联系的观点，从新的角度看过去的问题，使学生对于过去的知识有了新的认识，同时使新知识建立在已有知识的坚实基础上，形成良好的知识结构.

二是这种证法含有较多的数学思想方法，从直角三角形到锐角三角形，再到钝角三角形的推导过程完全按“分类讨论”的思想进行设置；通过作高将锐（钝）角三角形转化为直角三角形进行证明体现了“转化与化归”的思想；将三角形中的边角关系用数学式子进行表达体现了“形数化”的数形结合思想.特别是锐角三角形中，将所作的高置于两个直角三角形中分别计算，从而得出等式的方法体现了“算两次”的思想.“算两次”，又称富比尼（G.Fubini）原理.作为一种重要的数学解题方法，它实质上是方程思想的具体应用.

三是这种证法从特殊的直角三角形入手，通过“观察—归纳—猜想—证明”的过程，充分展现了知识发生、发展和形成的科学过程.同时归纳与演绎并用，突出了对学生思维能力的训练.史宁中认为：“思维训练主要靠两个能力，一个是演绎能力，一个是归纳能力”，而“从方法、思维角度来说，过去双基教育缺少了对归纳能力的培养，对学生未来走向社会不利，对培养创新人才不利.”教材所选择的证法恰恰较好地展现了“从特殊到一般”的归纳法的应用.

以上三个方面从一个角度体现了与时俱进地认识“双基”的新课标理念；更重要的是整个证明突出了对学生思维能力的培养，从而提高学生的数学素养和创新能力.这是数学学科有别于其他学科最显著的地方，也是新课标最重要的理念.当然也是考试大纲对学生能力的一个重要要求.可见，教材选用这种证法，确实是用心良苦.

三、证明方法不同阶段的呈现体现了“教师要从整体上把握教材”的理念

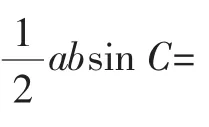
以上仅是我从正弦定理的证明所看到的新课标理念的一些变化.事实上，新课程以促进学生全面、持续、和谐的发展作为基本出发点，重视学生对数学全面正确的认识和理解，并更加关注学生在思维能力、情感态度与价值观等方面的发展与进步.同时更加注重应用，体现数学的文化价值，注重信息技术与数学课程的整合等.只要以新课标理念作指导，正确理解并从整体上把握教材，以探究引路，突出学生思维能力的培养，就一定能培养出具有一定数学素养的创新人才.

1.中华人民共和国教育部制订.普通高中数学课程标准（实验）［M］.北京：人民教育出版社，2003.

2.史宁中.《数学课程标准》的若干思考［J］.数学通报，2007（5）.

3.徐江培.展示知识发生发展的过程是数学教学的本质［J］.中国数学教育，2012（9）.