对一道自主招生题的另证和再推广
2013-07-25☉
中学数学杂志 2013年6期
☉
文[1]作者利用贝努利不等式得到命题1:设x1,x2,…,xk为实数,k为正整数,且x1+x2+…+xk=1,

在另证命题1之前先介绍一下凸函数的两个性质:
1.若函数y=f(x)在定义域D上二阶可导,则y=f(x)在D上为下凸函数的充分必要条件是f″(x)≥0.
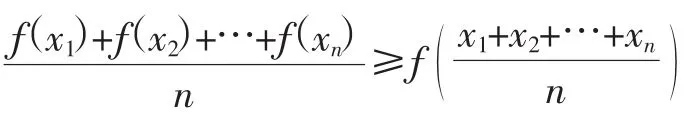
笔者利用下凸函数的性质另证命题1.

命题1得证.
利用下凸函数的性质可以将命题1推广为:
定理1 设x1,x2,…,xk为实数,k为正整数,且x1+x2+…+xk=1,α=2(tt≥1且t∈R),求证:
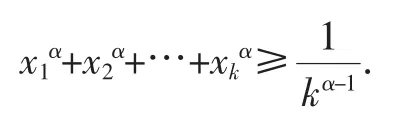
事实上,令f(x)=xα,则f″(x)=α(α-1)xα-2=2(t2t-1)x2t-2=2(t2t-1)(x2)t-1≥0.所以,由性质1知,f(x)在R上为下凸函数.于是,由性质2知,
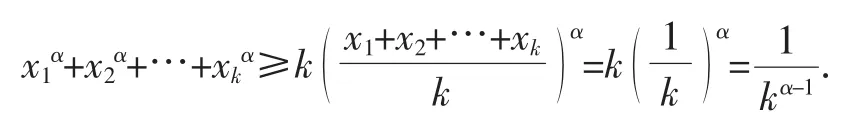
下面笔者再将文[1]的命题2推广为:
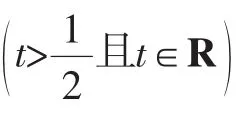
事实上,当x1,x2,…,xk全不为零,由[2]的权方和不等式知,
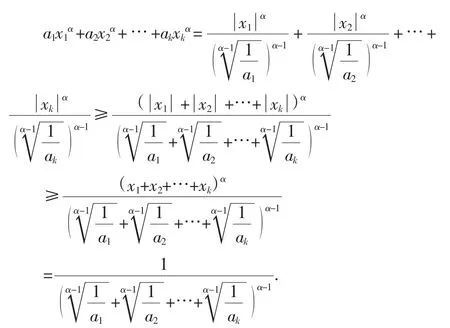
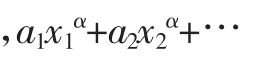
综上,定理2成立.
最后,笔者介绍一个稍微弱一点的定理:
定理3 设x1,x2,…,xk为正实数,a1,a2,…,ak为正实数,且x1+x2+…+xk=1,则
(1)当α>1或α<0时,
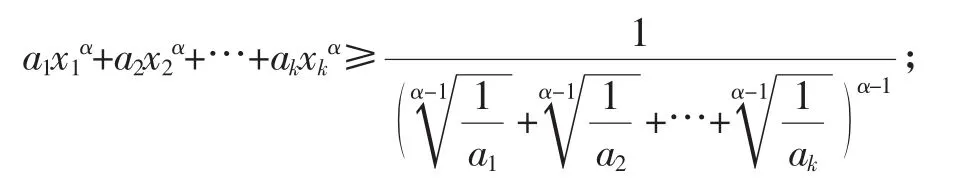
(2)当0<α<1时,

(1)的证明:事实上,由[2]的权方和不等式知,
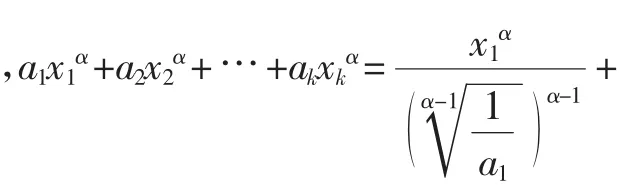
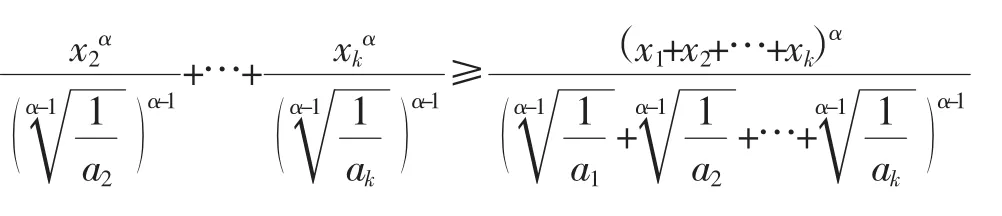
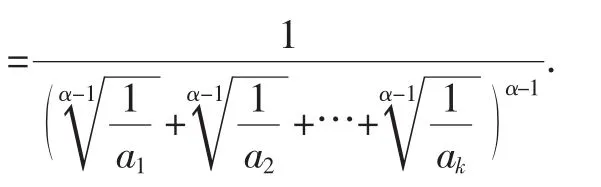
(2)的证明:事实上,由[2]的权方和不等式知,
当0<α<1时,a1x1α+a2x2α+…+akxkα
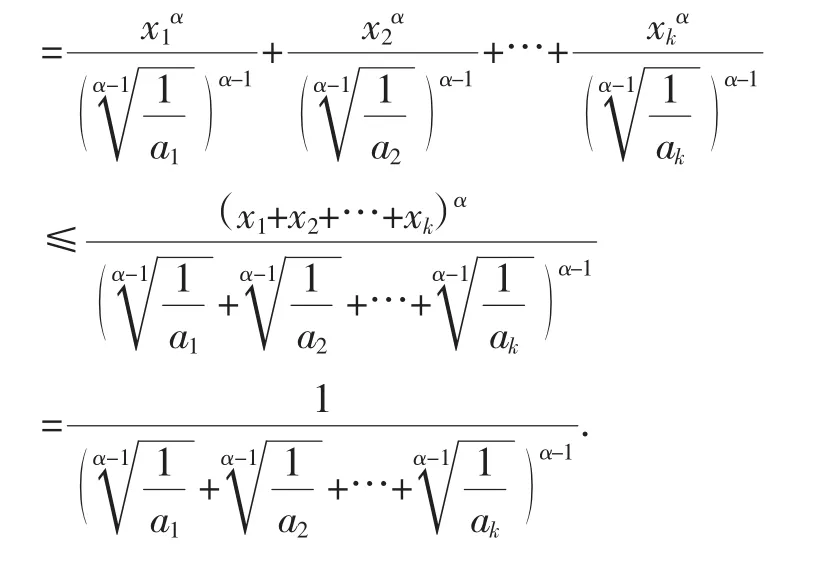
1.赵思林,李正泉.2009年清华大学自主招生一题的简解与推广[J].数学通讯(下半月),2010(11):53.
2.沈文选.走进教育数学[M].北京:科学出版社,2009:323.
