基于全状态观测器状态反馈的多轴转向极点配置

王吉华 魏民祥 杜言利 李玉芳

1.南京航空航天大学，南京，210016 2.山东理工大学，淄博，255049

0 引言

多轴形式越来越多地被公路运输、工程和军用等用途的车辆所采用，多轴转向是关键技术之一，多轴转向车辆的操纵稳定性控制已成为国内外专家学者关注的热点。对于已生产的多轴转向车辆，其总质量、长宽高、轴距、轮距和轮胎等结构和参数已确定，动力学模型及其稳定性和动态响应特性等也已基本确定，如想获得某些特定性能或对系统性能进行改善，则需对设计车辆进行附加控制。由于状态反馈包含了丰富的系统内部信息，在系统特征配置、系统镇定等方面具有很大优越性，故对多轴转向车辆采用状态反馈极点配置方法进行控制能有效改善系统的稳定性和动态品质。

国内外学者对多轴转向的控制进行了大量研究，并获得了一定的成果。An等［1］对三轴六轮独立转向采用理想横摆角速度跟踪、输出反馈和误差二次型目标函数优化方法进行控制；高秀华科研团队［2－3］对多轴转向车辆提出了基于降维观测器的最优控制和H2/H∞控制等，观测器重构状态用于最优控制；陈南科研团队［4－7］对四轮转向（4WS）提出了基于状态观测器的最优控制、μ综合鲁棒控制和滑膜鲁棒控制等；Hiraoka等［8］和Kazemi等［9］采用状态观测器进行状态重构并进行状态反馈，设计了滑膜控制器；Du等［10］和杜峰等［11］利用状态反馈分别进行H∞鲁棒控制和最优控制；范晶晶等［12］和李一染等［13］在转向控制研究中采用了输出反馈，分别进行包含PID的双重控制和自抗扰控制，但都没有提及极点配置。综上所述，目前专家学者对多轴转向提出很多控制算法，针对不同问题达到了很好效果，但均没有讨论极点配置控制问题。

基于状态反馈对极点进行任意配置，总能根据性能要求的希望极点得到相应控制器，适用范围广，算法简单，在离线求出控制器后的实际应用中只有加法和乘法运算，便于嵌入式编程，实时性好，实用性强。基于此，本文利用状态反馈的优越性，并考虑侧偏角难以测量的问题，提出基于全状态观测器进行状态反馈极点配置，从而改善多轴转向的性能。

1 问题描述

控制系统的建模和仿真采用多轴转向车辆二自由度线性单轨模型，理论和试验证明，在正常车速、小侧向加速度和小转向角下，基于该模型设计的控制器能正常工作［11］。建立单轨模型需作如下假设［14－15］：忽略悬架和转向系统作用，直接以各轴车轮转角为输入，车辆只做平行于地面的运动，且前进速度视为不变；由于正常行驶时侧向加速度均在0.4g以下，故轮胎侧偏特性为线性；不考虑车轮纵向力对轮胎侧偏特性的影响；忽略空气动力和轮胎回正力矩作用；各轴左右车轮均等效为轴中间单车轮，忽略左右车轮载荷转移及特性变化。经假设，车辆具有侧向和横摆两个运动自由度。

模型如图1所示，o为车辆质心，oxy为固定于车辆质心的车辆坐标系；o″为车辆转向中心到纵轴线的垂足；β为质心侧偏角；ωr为横摆角速度；u为质心前进速度；v为质心侧向速度；V为质心处的速度；Li为第i轴相对于质心的位移；δi为第i轴车轮转角；αi为第i轴车轮侧偏角；FYi为第i轴受到的侧偏力，i＝1，2，…，n。

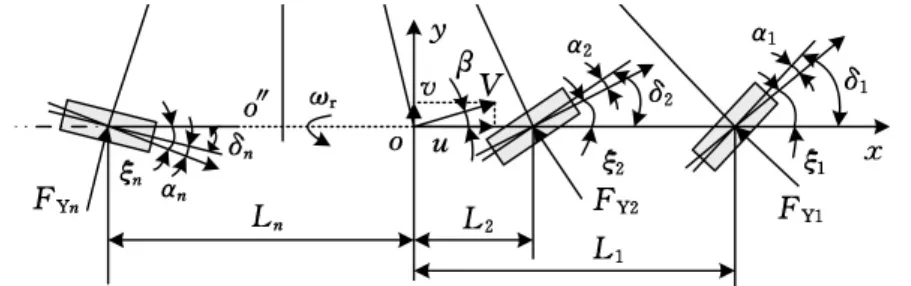
图1 多轴转向车辆二自由度动力学模型

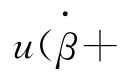
取横摆角速度ωr和侧偏角β为状态变量，又由于横摆角速度易测，故取ωr为输出，从以上车辆运动微分方程可得其状态空间表达式为

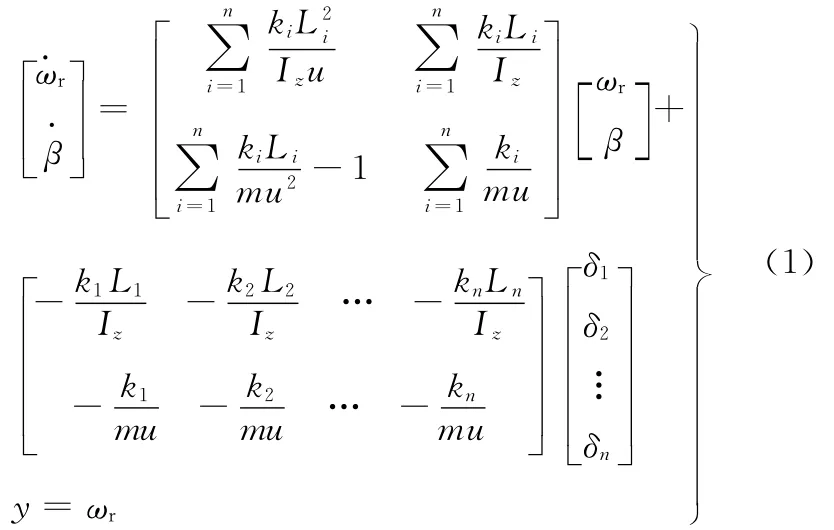
上述表达式中，δ1是前轮转角输入，δ2，δ3，…，δn是各后轴车轮转角。为了减小轮胎磨损，各轴车轮转角之间的关系满足阿克曼原理，即

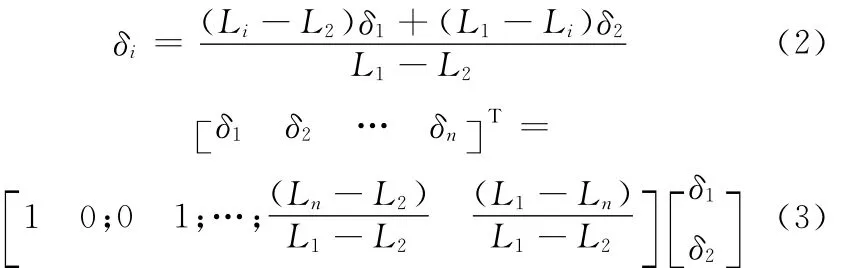
本文采用全后轴主动转向控制，于是驾驶者在前轮输入一定转角时，系统控制量输入就可由各后轴转角δ2，δ3，…，δn经过线性变化（式（3））等价为δ2。

多轴转向车辆基于全状态观测器的状态反馈控制系统如图2所示，v为整个闭环系统外部输入。为得到侧偏角β实现状态反馈，设计全状态观测器，令多轴转向车辆的输入r＝［δ1；δ2］和输出y＝［ωr］作为其输入，系统重构状态作为其输出；再利用观测器输出的重构状态，设计控制律K进行状态反馈系统极点配置。

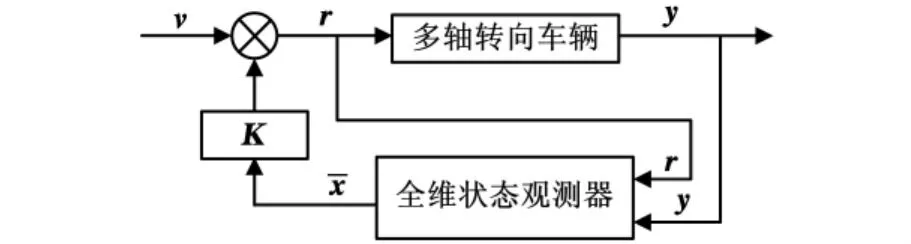
图2 基于状态观测器的状态反馈功能框图

2 控制器设计

2.1 全状态观测器设计

假设线性时不变系统状态空间表达式为

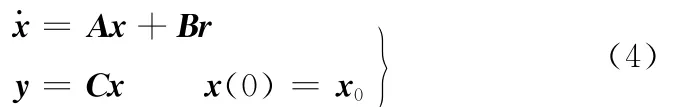
其中，状态x∈ Rn×1，输出y∈ Rq×1，输入r∈Rp×1，系统矩阵A∈ Rn×n，控制矩阵B∈ Rn×p，输出矩阵C∈Rq×n，x（0）为零时刻状态。

式（4）的全状态观测器如图3虚线框内所示［16］为估计状态，x为系统状态，则估计误差为＝x－，根据式（4），利用系统的输入r和输出y构造式（4）的模型系统，使估计误差满足：

图3 基于全状态观测器状态反馈结构图

利用y和模型系统输出之差进行反馈修正，形成闭环系统，即构造反馈阵G，得全状态观测器方程为

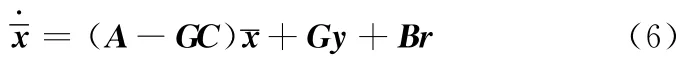
联立式（4）和式（6）得误差方程为

由式（5）可知，设计状态观测器就是设计反馈控制律G，使得：

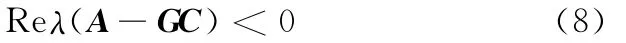
状态观测器响应时间应比系统（式（4））快，对观测器设计也采用极点配置方法；因在保持系统阻尼比不变情况下，增加固有振荡频率可缩短系统响应时间，所以取观测器希望极点是系统（式（4））希望极点的n′（n′＞1）倍，n′经调试确定，这不仅使观测器满足响应时间上的动态性能要求，也使式（8）得以成立。

定理1［16］全状态观测器极点任意配置。对于式（4）线性定常系统（A，B，C），全状态观测器极点可任意配置的充要条件是（A，C）完全可观测。

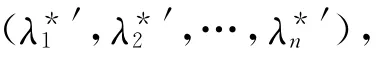
2.2 全状态观测器状态反馈控制器设计

重构状态后，系统（式（4））将利用重构状态进行状态反馈控制，见图3虚线框外部分，即设计线性状态反馈控制律r＝Kx＋v。

定理2［16］基于全状态观测器状态反馈进行极点任意配置。对于式（4）的线性定常系统（A，B，C）可利用全状态观测器的重构状态和线性状态反馈律r＝Kx＋v进行任意极点配置的充要条件是（A，B）完全可控。

由于系统的观测器和状态反馈具有分离特性［16］，故状态反馈控制律K和观测器反馈增益阵G的设计可分别单独进行，这样易知定理2的充要条件和系统极点配置算法。综合定理1和定理2，图3的整个闭环系统极点可任意配置充要条件是系统（式（4））完全可控和完全可观测。因本文对多轴转向车辆采用全后轴主动转向控制，又由式（3）知只含有一个控制量δ2和一个输出变量ωr，故可采用单变量系统极点配置算法。

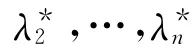
由性能要求可以确定车辆希望配置的极点，即状态反馈闭环系统极点，进一步可得全状态观测器希望极点，于是可按式（9）来求取K和G，G的求取应按模型系统的对偶系统极点配置来进行。

当考虑侧倾运动时，多轴转向车辆为三自由度线性模型，并采用全轮主动转向控制，需进行多变量系统极点配置，配置条件仍需满足定理1和定理2。但对多变量系统极点配置需分两步，先求取状态反馈阵K1，对某一输入ui，找到对应（A＋BK1，bi）可控对；然后针对闭环系统（A＋BK1，bi），按单变量系统极点配置求取K2，总配置矩阵为K1＋K2。同样，由分离特性［16］，全状态观测器可根据其对偶系统来进行相应的极点配置。

3 仿真验证

对某五轴转向车辆进行控制器求解和仿真试验，采用的主要参数如下：L1＝4379.3mm，L2＝1749.3mm，L3＝－0.7332mm，L4＝ －1860.7mm，L5＝－3720.7mm，k1＝－276.4k N/rad，k2＝k3＝k4＝k5＝ －360k N/rad，m＝39 280kg，Iz＝311 760 kg·m2。

对于式（4），δ2控制矩阵为B2，δ1控制矩阵为B1，可得：A＝ ［－1.8234 0.5433；－0.9913－1.9663］，B1＝ ［15.7683 －1.3817］，B2＝［－16.3116 3.3480］，B＝ ［B1；B2］，C＝［1 0］，直接传递矩阵D＝ ［0］。经计算，系统式（4）的极点为：［－1.8949＋0.7304j －1.8949－0.7304j］，系统（A，B2，C）可控性和可观性矩阵均满秩，完全可控和可观测，满足定理1和定理2，希望极点为λ＊＝［－3＋2j －3－2j］，观测器希望极点 为λ＊′＝2λ＊， 通 过 计 算，K＝ ［－0.0745 0.2973］，G＝ ［8.2102 58.4049］。

利用MATLAB/Simulink平台，分别建立五轴转向车辆开环、状态反馈闭环、基于全状态观测器状态反馈闭环以及输出反馈PID闭环系统的模型。图4所示是δ2＝0和δ1分别为1°、2°、3°、4°时开环阶跃响应，图5所示是δ1＝0和δ2分别为1°、2°、3°、4°时开环阶跃响应，开环系统稳定，但图4中稳态ωr/δ1约为5（°/s）/（°），稳态β/δ1约为－4，图5中稳态ωr/δ2约为 －5（°/s）/（°），稳态β/δ2大于4，±5% 误差范围调节时间约为3s，难以满足工程应用［14］。为了加快转向响应和调节状态稳态值，需对系统极点进行配置。

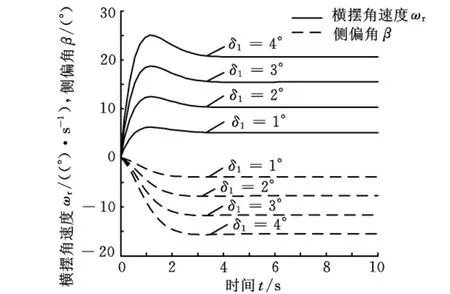
图4 开环系统前轮角阶跃输入响应

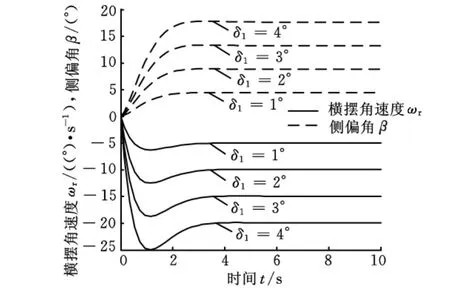
图5 开环系统后轮角阶跃输入响应

图6所示是δ1＝10°和u＝80km/h时，开环和状态反馈控制仿真对比，状态反馈±5%误差范围调节时间小于0.25s，比开环的3s缩短很多，转向响应迅速；ωr和β稳态输出分别约为2.3°/s和－0.043°，比开环要小很多；稳态β/δ1≈0，稳态ωr/δ1≈0.23（°/s）/（°），转向平稳；图7所示是状态反馈控制量δ2曲线，其最大值约为－2.8°（负号表方向），工程易实现；综合可知，状态反馈极点配置满足工程应用要求，达到控制效果。

图6 开环系统和状态反馈前轮角阶跃输入响应

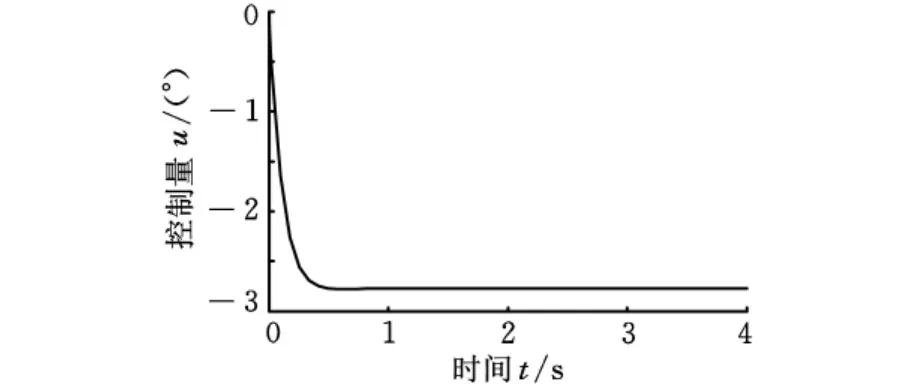
图7 状态反馈控制量曲线

图8所示是δ1＝10°和u＝80km/h时，对状态反馈和基于全状态观测器状态反馈进行仿真的曲线，两者状态响应完全重合，说明基于全状态观测器的状态反馈仍保持原状态反馈的控制品质，也证明了观测器和状态反馈的分离特性。

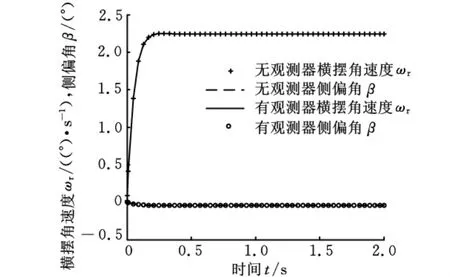
图8 前轮角阶跃输入重构状态和实际状态

图9所示是δ1＝10°和u＝80km/h时，观测器估计状态和车辆实际状态曲线，图10所示是估计状态和实际状态误差曲线。ωr和β稳态估计误差分别是0.08°/s和－0.0022°，相对误差绝对值分别为3.48%和5.12%，状态估计曲线比实际状态曲线略有提前到达稳态值，说明全状态观测器跟踪实际状态精度较高，误差为5%左右，跟踪稳态值速度比实际状态响应快。

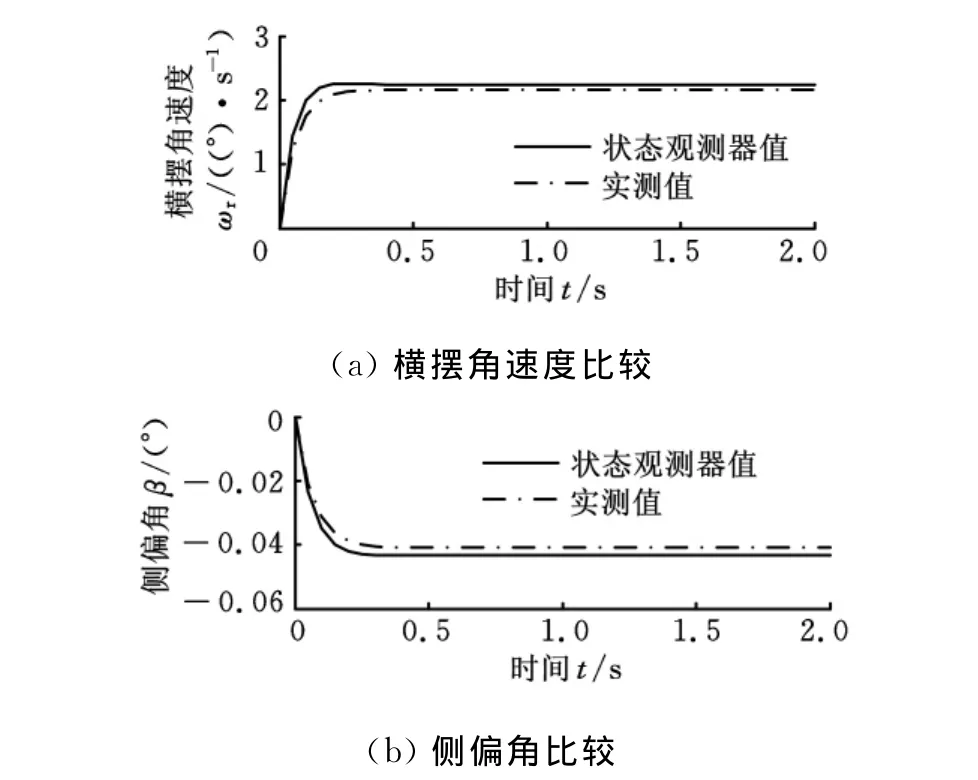
图9 状态估计值和实际状态值比较

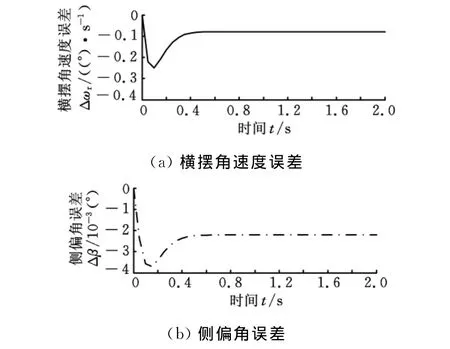
图10 状态估计误差曲线图

图11所示是δ1＝10°和u＝80km/h时，车辆ωr输出反馈PID控制和观测器状态反馈控制的仿真结果比较。给定PID希望输入是ωr＝2.5°/s，经反复调试，当比例系数Kp＝0.001、积分系数Ki＝0.0001和微分系数Kd＝0.05时，PID控制效果相对最好，±5%误差范围调节时间约为1s，比开环控制有所减小，但比全状态观测器状态反馈大很多，稳态ωr为5.6°/s，而且稳态β值为－3.4°，比全状态观测器状态反馈大很多，均与工程应用相违背，说明PID在响应时间和稳态值上都难以对样车达到希望的控制效果，对操纵稳定性控制明显比全状态观测器状态反馈差。

图11 PID和观测器状态反馈前轮转角阶跃输入响应

图12所示是δ1分别为5°和10°、u＝80km/h且在δ2加入0.573sint干扰的输出反馈PID控制响应，说明在很小干扰下系统就处于临界稳定状态，抗干扰能力差。图13所示是δ1＝10°、u＝80km/h以及输出反馈PID控制δ2加入0.573sint干扰而观测器状态反馈δ2加入5.73sint干扰的状态响应比较，结合图8，观测器状态反馈控制的ωr和β响应均不发生改变，能抵抗±5.73°范围内的外界干扰。

图12 外界干扰下PID控制不同前轮转角阶跃输入响应

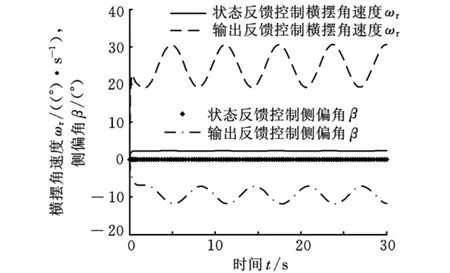
图13 外界干扰下PID和观测器状态反馈控制响应

图14所示是δ1分别为5°和10°、u＝80km/h和δ2加入5.73sint干扰的观测器状态反馈控制响应，在此干扰下，ωr分别约为1.75°/s和2.3°/s，β≤0.05°，在不同前轮转角下均具有抗干扰能力，满足工程应用要求。综合可知，PID控制在不同前轮输入下均很难抵抗外界干扰，鲁棒性差，而观测器状态反馈控制在不同前轮输入下均能在±5.73°范围内抵抗外界干扰，具有一定的鲁棒性，能在侧向风、横向斜坡和转向机构变形等引起的较小外界干扰下保持系统控制性能。

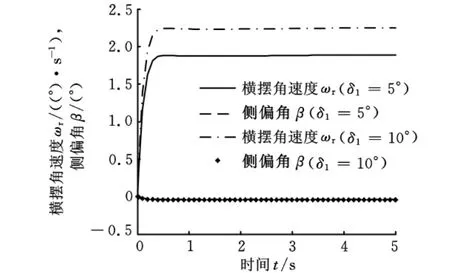
图14 外界干扰下观测器状态反馈不同前轮转角输入响应

4 结论

根据多轴转向车辆的横摆角速度易测而侧偏角不易测特点，设计了全状态观测器；在此基础上，基于状态反馈的优越性，设计状态反馈控制器进行极点配置。建立控制系统模型和求解控制器，通过对某五轴转向车辆实例仿真，将全观测器状态反馈与开环系统、状态反馈和PID控制进行对比，结果表明全状态观测器跟踪实际状态的效果好，设计的控制器在响应时间和稳态响应值上能有效改善多轴转向开环系统的性能，能实现PID难以达到的控制效果，且具有一定的鲁棒性，此方法极点可任意配置，用于改善的性能范围广，且易用嵌入式系统编程实现控制算法，实用性强，具有较好的工程应用价值。

［1］An S J，Yi K，Jung G，et al.Desired Yaw Rate and Steering Control Method during Cornering for a Six－wheeled Vehicle［J］.International Journal of Automotive Technology，2008，9（2）：173－181.

［2］李炎亮，高秀华，李占江，等.最优跟踪车载式自行火炮多桥动态转向系统［J］.吉林大学学报（工学版），2006，36（增刊2）：36－40.

Li Yanliang，Gao Xiuhua，Li Zhanjiang，et al.Optimal Tracking Multi－axle Dynamic Steering System of Truck－howitzer［J］.Journal of Jilin University（Engineering and Technology Edition），2006，36（S2）：36－40.

［3］王云超，高秀华，胡景煌，等.多轴转向车辆转向系统的H2/H∞混合控制［J］.重庆工学院学报（自然科学版），2008，22（8）：6－10.

Wang Yunchao，Gao Xiuhua，Hu Jinghuang，et al.MixedH2/H∞Control for Multi－axle Steering Vehicle［J］.Journal of Chongqing Institute of Technology（Natural Science），2008，22（8）：6－10.

［4］殷国栋，陈南，李普.基于降阶观测器的四轮转向车辆随动操纵瞬态稳定性分析［J］.中国机械工程，2004，15（14）：1298－1301.

Yin Guodong，Chen Nan，Li Pu.Transient Follow Handling Stability Analysis for Four－wheel Steering Vehicle Based on Reduced Order Observer［J］.China Mechanical Engineering，2004，15（14）：1298－1301.

［5］李普，陈南，孙庆鸿.基于状态观测器的4WS车辆最优随动操纵研究［J］.机械工程学报，2004，40（1）：50－55.

Li Pu，Chen Nan，Sun Qinghong.Optimal Follow up Control of 4WS Vehicle Based on State Estimator［J］.Chinese Journal of Mechanical Engineering，2004，40（1）：50－55.

［6］殷国栋，陈南，李普.基于μ综合鲁棒控制的四轮转向车辆操纵稳定性研究［J］.中国工程科学，2005，7（4）：54－58.

Yin Guodong，Chen Nan，Li Pu.Handling Stability for Four－wheel Steering Vehicle Based onμSynthesis Robust Control［J］.Engineering Science，2005，7（4）：54－58.

［7］陈建松，陈南，殷国栋，等.考虑非线性特征的4WS车辆滑模鲁棒稳定性控制［J］.东南大学学报（自然科学版），2010，40（5）：969－972.

Chen Jiansong，Chen Nan，Yin Guodong，et al.Sliding－ mode Robust Control for 4WS Vehicle Based on Non－linear Characteristic［J］.Journal of Southeast University （Natural Science Edition），2010，40（5）：969－972.

［8］Hiraoka T，Nishihara O，Kumamoto H.Automatic Path－tracking Controller of a Four－wheel Steering Vehicle［J］.Vehicle System Dynamics，2009，47（10）：1205－1227.

［9］Kazemi R，Janbakhsh A A.Nonlinear Adaptive Sliding Mode Control for Vehicle Handling Improving via Steering－by－wire［J］.International Journal of Automotive Technology，2010，11（3）：345－354.

［10］Du Haiping，Zhang Nong，Naghdy F.Velocitydependent Robust Control for Improving Vehicle Lateral Dynamics［J］.Transportation Research Part C：Emerging Technologies，2011，19（3）：454－468.

［11］杜峰，魏朗，赵建友.基于状态反馈的四轮转向汽车最优控制［J］.长安大学学报（自然科学版），2008，28（4）：91－94.

Du Feng，Wei Lang，Zhao Jianyou.Optimization Control of Four－wheel Steering Vehicle Based on State Feedback［J］.Journal of Chang'an University（Natural Science Edition），2008，28（4）：91－94.

［12］范晶晶，罗禹贡，张海林，等.全轮独立电驱动车辆双重转向控制策略的研究［J］.汽车工程，2011，33（5）：369－372.

Fang Jingjing，Luo Yugong，Zhang Hailin，et al.A Research on the Dual－Steering Control Strategy for All－ Wheel Independent Electric Drive Vehicle［J］.Automotive Engineering，2011，33（5）：369－372.

［13］李一染，陈慧，高博麟.自抗扰控制在前轮主动转向控制中的应用 ［J］.汽车工程，2011，33（5）：372，388－391.

Li Yiran，Chen Hui，Gao Bolin.Application of Active Disturbance Rejection Control to Active Front Steering Control［J］.Automotive Engineering，2011，33（5）：372，388－391.

［14］余志生.汽车理论［M］.北京：机械工业出版社，2000.

［15］郭孔辉.汽车操纵动力学［M］.长春：吉林科学技术出版社，1991.

［16］姜长生，孙隆和，吴庆宪，等.系统理论与鲁棒控制［M］.北京：航空工业出版社，1998.