Nyquist 稳定判据的分析与应用
2022-07-30郑恩让
郑恩让 陈 蓓 张 玲
(陕西科技大学 电气与控制工程学院, 西安 710021)
“自动控制原理”是自动化、电气工程及其机器人工程等专业的重要的基础课,是“运动控制系统”“过程控制”等系统分析与设计的基础理论课。在“自动控制原理”课程中,稳定性分析是最重要的内容之一。在时滞过程、网络信息处理中,系统不可避免会存在信号、信息的传输延迟。若系统中含有纯滞后环节,采用劳斯判据就不能方便的对系统进行稳定性分析。尤其是当开环系统传递函数为
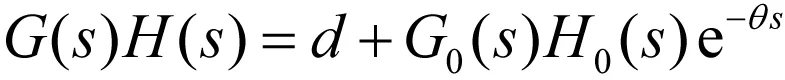
(1)
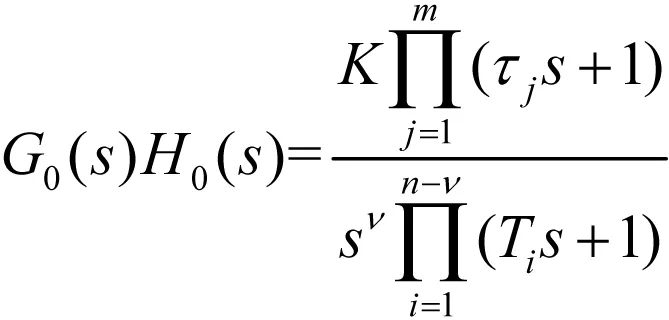
(2)
其中当n≥m,K>0,Ti>0,τj>0,d为实常数时,系统稳定性不容易判定。而学生若对Nyquist
稳定判据能够理解充分,则求解此类问题就会迎刃而解。
1 问题与分析
问题提出:已知某负反馈控制系统的开环传递函数为
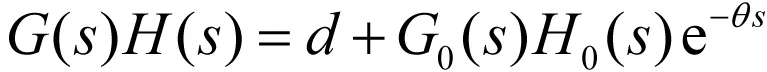
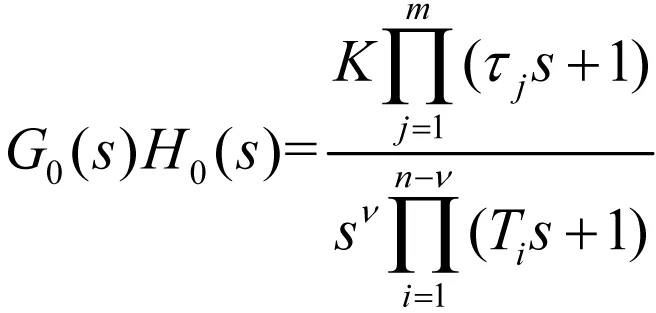
其中n≥m,K>0,Ti>0,τj>0,判定闭环系统的稳定性。
在课程未讲授Nyquist 稳定判据判之前,对这类系统判定闭环系统稳定性并不容易[1]。这是因为系统的闭环特征方程中含有e-θs这一因子,使闭环特征方程变为超越方程,求根或用劳斯判据都不
容易。
Nyquist 稳定判据:反馈控制系统稳定的充分必要条件是半闭合曲线不穿过(-1,j0)点,且逆时针包围临界点(-1,j0)的圈数N等于开环传递函数的正实部极点数P。
采用开环幅相频率特性对(-1,j0)点的包围周数,即可判定闭环系统的稳定性,因为闭环系统稳定时,其在右半S平面的闭环极点数为零,即式N=P-Z中Z=0。实际中,只需绘制ω=0→∞时的开环幅相频率特性曲线即可。而ω=-∞→∞时,开环幅相频率特性曲线绕(-1,j0)点顺时钟转过的周数,等于ω=0→∞时开环幅相频率特性曲线绕(-1,j0)点顺时钟转过的周数乘以2。
当系统开环传递函数含有纯滞后环节时,系统的幅频特性不变,相频特性产生滞后[2],因此,绘制出含有纯滞后环节的开环系统幅相频率特性,即可采用Nyquist稳定判据判定闭环系统的稳定性。

通过以上分析,可以通过绘制开环系统的幅相频率特性,利用Nyquist稳定判据判定开环系统含有纯滞后环节、平移和纯滞后环节时闭环系统的稳定性。
2 Nyquist稳定判据的应用
例1:某单位负反馈控制系统的开环传递函数为
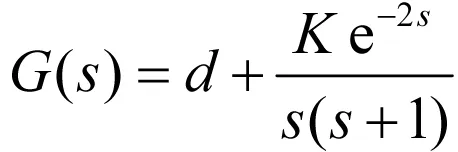
(3)
试分别确定d=-0.5,0,1时,使闭环系统稳定的K的取值范围。
解答:本题考查对奈奎斯特判据的推导和理解。
由于系统含有纯滞后环节,因此,要采用奈奎斯特判据。
系统的闭环特征方程为:
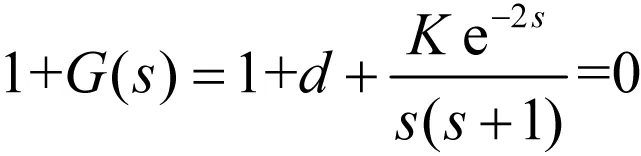
(4)
整理得:
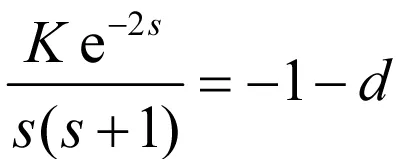
(5)
与前面分析的Nyquist判据比较可得,只要等效的开环频率特性包围(-(1+d),j0),则闭环系统一定不稳定。
等效开环传递函数为:
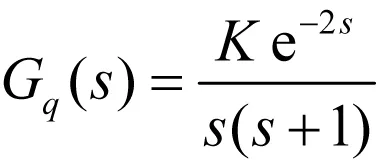
(6)
其相频特性为:
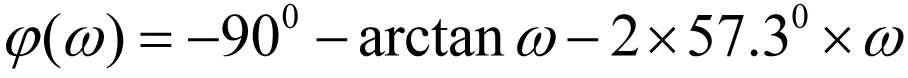
令

解之得,ω=0.54 rad/s。
等效开环幅频特性为:
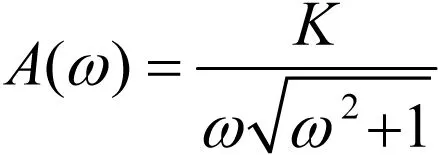
(7)
欲使闭环系统稳定,则要
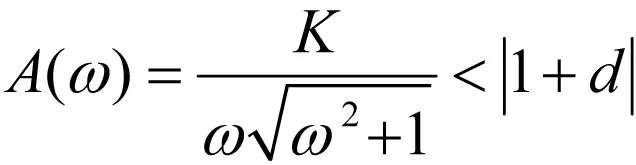
(8)
当d=-0.5时,解之得,0 当d=0时,解之得,0 当d=1时,解之得,0 例2:定性说明纯滞后特性对系统性能的影响。 解答:设系统的开环传递函数为 (9) (10) n≥m,K>0,Ti>0,τj>0 则有,系统的开环相频特性为 (11) 系统的开环幅频特性为 (12) 由系统的开环幅频、开环相频特性可知,纯滞后环节不影响系统的幅频特性,而只影响系统的相频特性。因此,纯滞后环节的存在,会使系统的相角裕度减小,故闭环系的稳定性、过渡过程特性会变差。 在我校自动化专业17级教改班“自动控制原理”课程中通过讲授Nyquist稳定判据,并对其进行推导和证明,紧接着对本文提出的开环系统含有纯滞后环节、含有位移和纯滞后环节的闭环系统稳定性进行判定,学生易于理解和掌握。尤其是通过引入F(s)=(1+d)+G(s)H(s),学生立即明白了通过绘制等效开环系统的Nyquist曲线,研究曲线对(-(1+d),j0)的环绕情况就可判定开环含有纯滞后环节、含有平移和纯滞后环节时闭环系统的稳定性。通过教师对Nyquist判据的讲授与分析,结合实际示例,使学生对判据的理解更加深刻,学习效果明显提高,期末考试该知识点成绩较16级非教改班平均提高4.2分。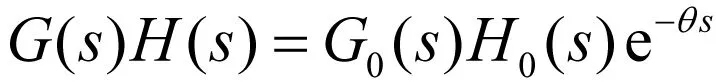
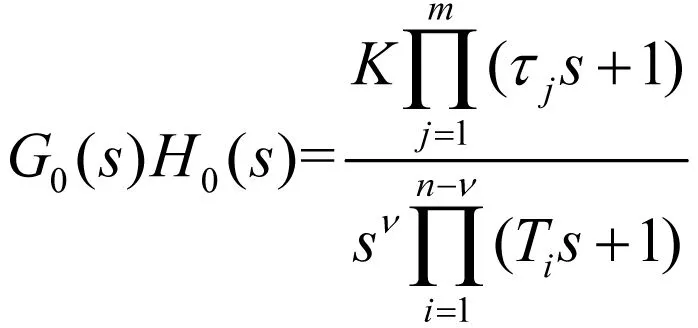
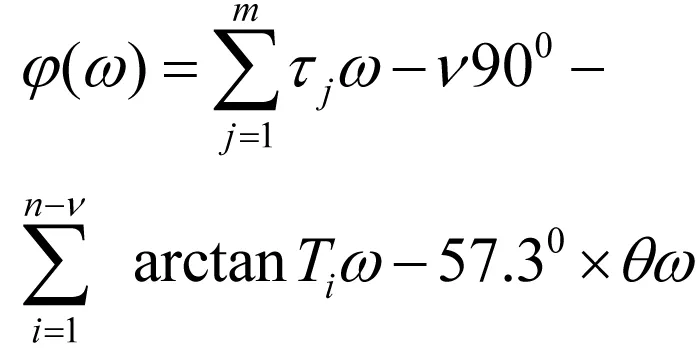

3 结语
