基于半径变化量测量的圆度误差最小外接圆评定法研究
2013-07-24张玉梅
张玉梅
(赤峰学院建筑与机械工程学院,内蒙古赤峰024000)
基于半径变化量测量的圆度误差最小外接圆评定法研究
张玉梅
(赤峰学院建筑与机械工程学院,内蒙古赤峰024000)
最小外接圆法是一种工程中常用的圆度误差评定方法.文章给出了基于半径变化量测量的圆度误差最小外接圆评定法的数学模型和最小外接圆的判定方法和条件.实验结果表明,给出的数学模型是正确的,判定条件是合理可行的.
最小外接圆法;半径变化量测量;圆度误差
1 前言
根据国家标准GB/T7235-2004,圆度误差主要有四种评定方法,分别是最小区域圆法、最小二乘圆法和切接圆法(包括最小外接圆法和最大内接圆法)[1].其中最小外接圆法是工程中常用的一种方法,主要用于轴类零件的圆度误差评定,相当于基孔制的轴孔配合情况[2].
按采样方式不同,圆度误差的精密测量有坐标测量法和半径变化量测量法[3].本文将在最小二乘圆法的基础上,研究基于半径变化量测量方式的圆度误差最小外接圆评定法的数学模型,讨论最小外接圆的判定条件.
2 最小外接圆法圆度误差评定数学模型
最小外接圆法圆度误差评定数学模型在最小二乘圆法基础上给出.
所谓最小二乘圆法,是指根据实际被测轮廓上各测量点到最小二乘圆的径向距离平方和最小的原则,首先确定最小二乘圆,据此确定的圆度误差值等于实际被测点到最小二乘圆的径向距离最大值(正)与最小值(负)的差值,如图1所示.
根据文献[3],基于半径变化量测量的最小二乘圆圆心坐标O0(x0,y0)和最小二乘圆半径R0分别为:

式中M表示测量一周的采样点数;
j表示采样点序号,j=1,2,…,M;
r0表示第一个测量点至回转中心的距离;
ΔRj表示任一测量点相对于第一个测量点的半径变化量.
θj表示任意测量点与第一个测量点间的夹角;
任意测量点Pj相对最小二乘圆的径向偏差值δj为:
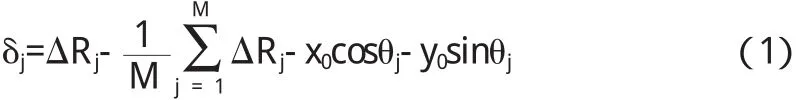
最小二乘圆法评定的圆度误差E0的数学模型为:
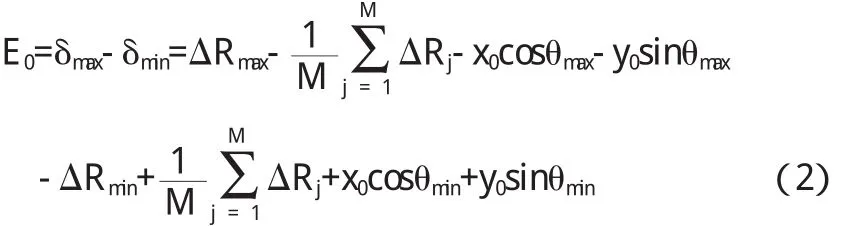
式中ΔRmax,ΔRmin分别表示实际被测点到最小二乘圆的最大偏差值点和最小偏差值点相对于第一测量点的半径变化量;
θmax,θmin则表示与ΔRmax,ΔRmin相对应的测量点角坐标.
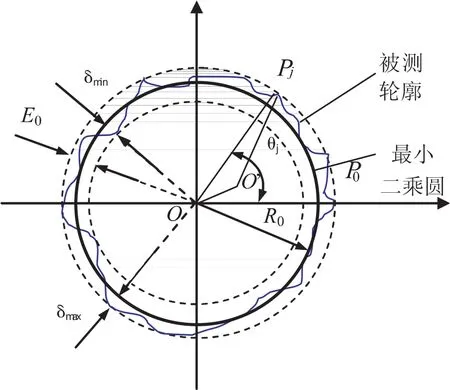
图1 最小二乘圆法圆度误差评定原理图
最小外接圆法的评定过程是:先作实际被测轮廓的最小外接圆,然后作与最小外接圆同心的被测轮廓的最大内包容圆,两同心圆的半径差,就是最小外接圆法评定的圆度误差,如图2所示.O1是最小外接圆圆心,R1是最小外接圆半径,Rmin是与最小外接圆同心的被测轮廓最大内包容圆的半径,即被测点中到最小外接圆径向距离最大点所对应的半径.按此方法评定圆度误差E1计算式为:

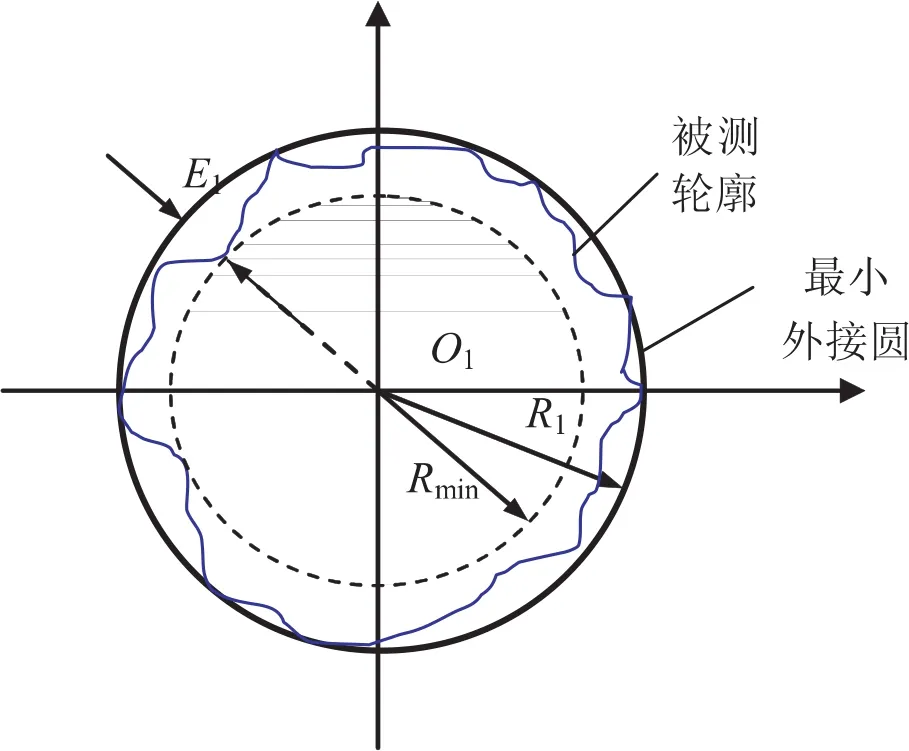
图2 最小外接圆法圆度误差评定原理图
按照确定最小二乘圆的方法,加上最小外接圆的判断条件来确定最小外接圆,得到基于半径变化量测量的最小外接圆法圆度误差评定数学模型为:
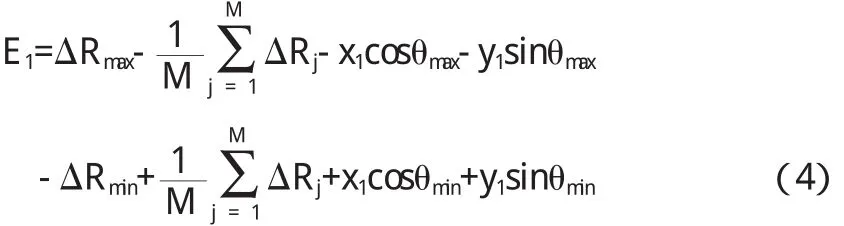
式中M、j、ΔRj同上;
(x1,y1)表示最小外接圆的圆心坐标;
ΔRmin表示位于同心最大内包容圆上的测量点的半径变化量测量值;
θmin表示与ΔRmin相应测量点的角坐标值.
ΔRmax表示位于最小外接圆上的测量点的半径变化量测量值;
θmax表示与ΔRmax相应测量点的角坐标值;
根据文献[4],最小外接圆的判断准则有两种,分别为:
(1)对径准则.外接圆与被测轮廓两点相接,且此两点连线为外接圆直径.
(2)三角形准则.外接圆与被测轮廓三点相接,此三点相连后形成锐角或直角三角形.
测量点属于外接圆和被测轮廓接触点的判断方法是:被测沾到最小二乘圆偏差值最大且相等.
基于半径变化量测量的最大偏差值计算式为:
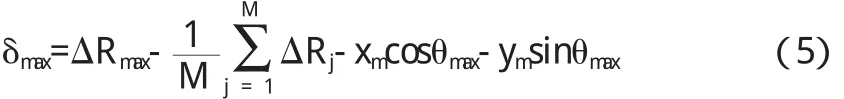
式中(xm,ym)表示外接圆圆心坐标.
3 最小外接圆判定方法
3.1 对径准则的判定方法
若被测点中有两点(A和B)与最小二乘圆的径向偏差值最大且相等,即
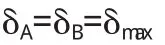
同时,此两点的角坐标满足式(6),

则判断此圆是最小外接圆.否则,按下面方法进行判断.
3.2 三角形准则的判定方法
若被测点中有三点(A、B和C)与最小二乘圆径向偏差最大且相等,即

则首先将三点的角坐标θA,θB,θC按由大到小的顺序排列,比如θA>θB>θC,然后按照下列条件判断是否满足锐角或直角三角形准则.
条件1若θA-θC=180°,则A、B、C三点连线会构成直角三角形,如图3所示(设θC=0°),说明此时的外接圆是最小外接圆.
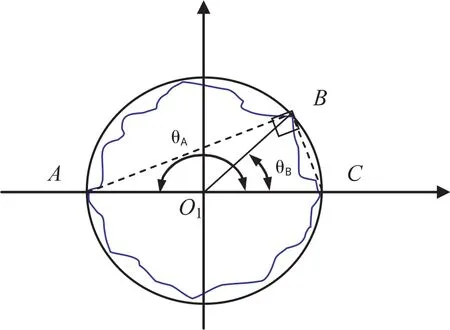
图3 三角形准则最小外接圆判定条件1
条件2:若同时成立,则A、B、C三点连线构成锐角三角形(如图4(a))或直角三角形(如图4(b))(设θC=0°),可以判定此外接圆为最小外接圆.

图4 三角形准则最小外接圆判定条件2
条件3若θA-θC<180°,如图5所示(设θC=0°),说明A、B、C连线会构成钝角三角形,则说明此外接圆不是最小外接圆.
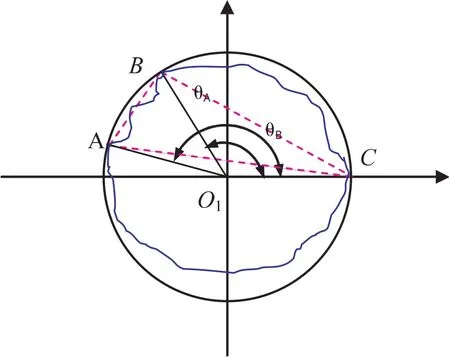
图5 三角形准则最小外接圆判定条件3
条件4若θB-θC>180°,如图6所示,(设θC=0°),说明A、B、C连线构成钝角三角形,说明此外接圆不是最小外接圆.
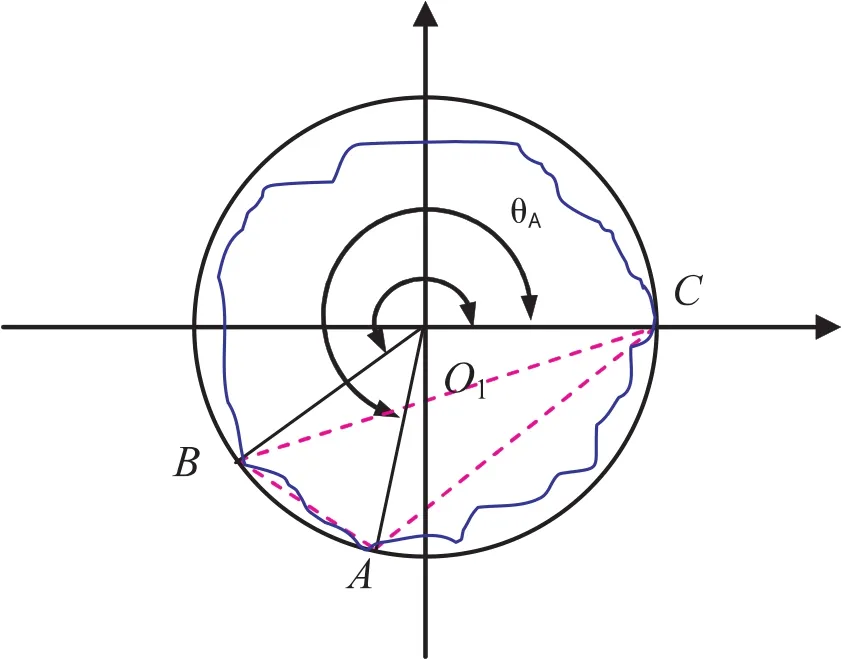
图6 三角形准则最小外接圆判定条件4
最小外接圆判定条件汇总结果见表1.

表1 最小外接圆判定条件
3.3 最小外接圆与被测轮廓接触点数多于三点时的判定方法
当外接圆和被测轮廓接触点数量超过三点时,将所有接触点的角坐标排序,三个一组,按一个方向逐次判断.只要出现一组满足表1所列最小外接圆成立条件即可.
4 实验验证
将圆度误差的半径变化量测量数据,经过滤波等数据处理后,得实际轮廓,再根据前文给出的圆度误差最小外接圆评定法数学模型和最小外接圆判定条件,通过优化算法得到最小外接圆,结果如图7所示.A、B、C三点满足三角形准则中的判定条件2.

图7 被测轮廓与最小外接圆
5 结论
针对圆度误差的半径变化量测量法,研究了工程中常用的圆度误差最小外接圆评定法的数学模型,并给出了最小外接圆的判定条件.实验结果表明,给出的基于半径变化量测量的圆度误差最小外接圆评定法的数学模型是正确的,最小外接圆的判定方法和条件是合理可行的.研究结果对基于半径变化量测量的圆度误差评定方法研究有重要的应用价值.
〔1〕GB/T7235—2004,产品几何量技术规范(GPS)评定圆度误差的方法[S].中华人民共和国国家质量监督检验检疫总局,2004.
〔2〕方沁林.圆度误差评定的算法研究与软件设计[D].武汉:华中科技大学,2007.
〔3〕甘永立.形状和位置误差检测[M].北京:国防工业出版社,1995.
〔4〕曹麟祥,王丙甲.圆度检测技术[M].北京:国防工业出版社,1998.
TB92
A
1673-260X(2013)11-0013-03
