延性金属渐进破坏试验与数值研究

刘 超， 孙 秦， 刘彦杰， 范学领

（西北工业大学航空学院，西安 710072）

其中f为第一主应力不变量I1和第三偏应力不变量J3某种形式的函数;εp表示等效塑性应变;εpf表示断裂发生时材料点的等效塑性应变。其中εp反映了第二偏应力不变量J2的影响。结合EWK和X-W两种延性断裂模型的各自特点，同时采用EWK模型中的损伤与塑性过程非耦合的损伤累积理论提出了一种同样基于三应力不变量的延性断裂模型。

改进的三应力不变量延性断裂模型依据X-W模型的断裂包线形式，其中综合考虑到静水压力和Lode角的影响。其断裂包线εf表达式定义为:

在表达式（7）中εf0为静水压力p为零时的断裂应变 ，μp（p）为静水压力 p的函数，μθ（θ）为 Lode角θ的函数，其表达式为:

裂纹是引起航空航天领域中各种金属结构、零部件失效的重要因素。因此，掌握裂纹扩展的规律及控制裂纹的扩展在工程应用上具有重要意义。金属板材的单向拉伸试验为结构寿命分析和剩余强度计算提供了基本数据参考。因此，模拟金属板材在单向拉伸状态下的裂纹形成与扩展直至完全断裂的全过程是一个不可或缺的内容。在工程应用中，金属薄板通常简化为完全平面应力状态进行力学分析。然而从严格意义上讲，这种简化只适用于很薄且尺寸较大的薄板。随着薄板的厚度增加，有限厚度的金属板材的断裂过程比平面应力状态下更加复杂，在三维状态下进行有限元数值计算比二维情况下能更好地反映板材沿厚度方向上的裂纹扩展情况。

Taira和Tanaka［1］应用断裂力学方法研究了在拉伸状态下含初始裂纹的金属板裂纹尖端应力分布及厚度对材料断裂韧性地影响。Pardoen［2，3］等研究了不同厚度的铝合金6082T0含双边初始裂纹的薄板试件的载荷位移曲线并与试验曲线进行了对比分析，并研究了J积分的变化。上述文章均采用断裂力学方法进行研究，这就决定了所选薄板试件必须含有初始裂纹。而针对无初始裂纹的光滑薄板在拉伸状态下从裂纹萌生和扩展直至断裂的全过程，应用断裂力学的分析方法就显出其局限性。因此，基于连续介质损伤力学破坏准则与有限元数值计算相结合成为预测工程结构在复杂载荷条件下渐进破坏过程的最有效技术途径。一系列关于韧性材料构件的失效机理的研究和适用与韧性材料的断裂准则被相继提出，并应用于模拟和预测构件的失效行为［4～9］。但是，这些文献中均未综合考虑静水压力和Lode角在韧性材料断裂过程中对损伤变量的作用。Kamoulakos在 E-W［10］模型的基础上，提出了EWK［11］模型。该模型认为裂纹的萌生和扩展直至完全断裂是材料的连续特性，并认为材料应变损伤累积到断裂阀值时导致结构断裂。Xue和Wierzbicki［12］在研究大量断裂模型基础上，提出了一种新的断裂模型（X-W模型），该模型提出了断裂包线的概念以及损伤与塑性过程耦合的损伤累积理论，并给出了归一化的损伤累积模型。这两个基于连续损伤力学理论的延性破坏模型包含了3个应力不变量对塑性破坏的影响作用，并考虑了Lode角和静水压力的作用，因此其适用性更强，但各自也有其局限性。

为更好地数值模拟金属构件的静力渐进破坏过程，本文依然保留X-W断裂模型的断裂包线形式，同时为了便于工程应用，采用EWK模型中的损伤与塑性过程非耦合的损伤累积理论。提出了一种改进的3应力不变量延性金属断裂模型。通过ABAQUS用户材料子程序VUMAT将该改进模型嵌入有限元显式算法（准静态）主程序，并应用于铝合金2A12-T4板材的静力破坏过程的模拟，最后与试验结果进行了对比分析。

1 基于连续损伤力学的延性断裂模型

1.1EWK 模型

EWK延性断裂模型认为结构中微小裂纹的萌生和扩展，直至完全断裂是材料应变损伤不断累积而产生的结果［13］。EWK延性断裂模型的一般表达式如下:

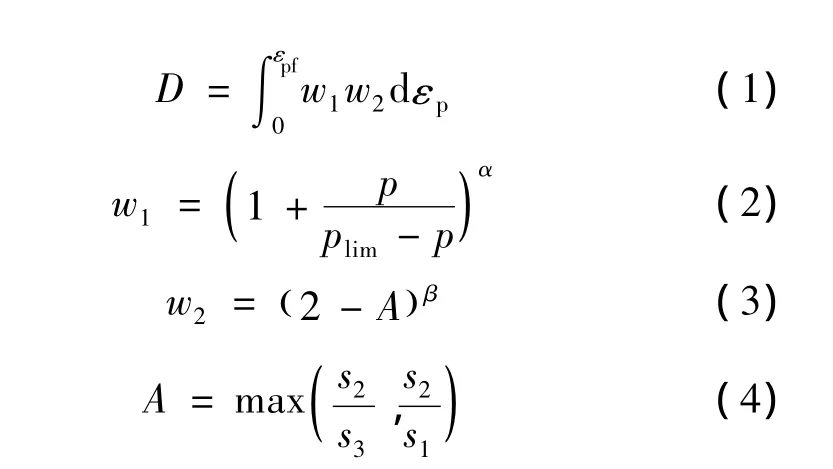
其中s1＞s2＞s3，si为主偏应力，εp为等效塑性应变，εpf为断裂时的等效塑性应变，α，β均为材料常数，p为材料点的静水压力，plim也是材料常数，代表了无缺陷时理想状态的极限静水压力。当损伤变量D达到临界值Dc时材料点发生断裂。EWK模型采用损伤与塑性过程非耦合的损伤累积理论，即材料的弹塑性应力应变关系独立于损伤变量的演化。因而较易与工程应用相结合，以决定其材料参数，但不具备断裂包线的概念。

1.2X-W 模型

X-W延性断裂模型由麻省理工大学的Xue和Wierzbick提出，该模型采用损伤变量与材料塑性变形过程相耦合的损伤累积理论，并建立了相应的积分型断裂准则。该准则中提出了两个重要的概念，其一是断裂包线，其二是建立了相应的损伤演化规则。其表达式如下:

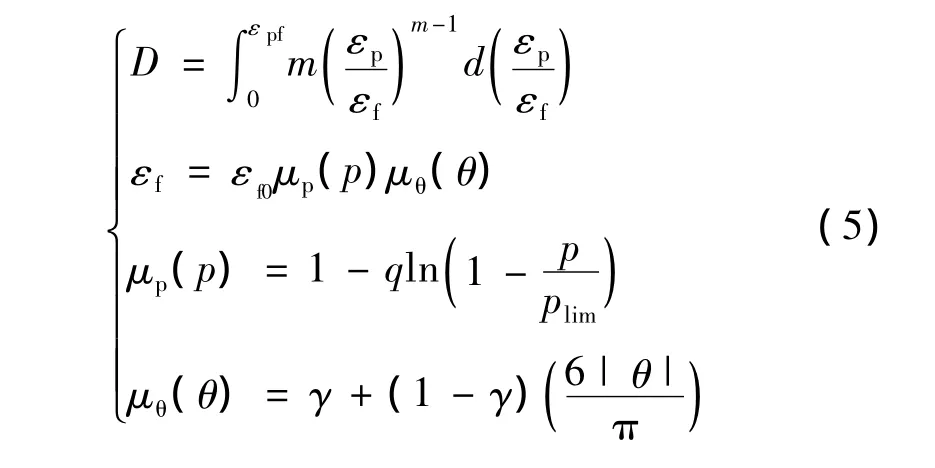
其中μp（p）为静水压力函数，μθ（θ）为关于Lode角θ的函数。plim，γ，q，m均为材料常数，εf为断裂包线，εf0为静水压力为零时的断裂应变。当损伤变量D=1时材料点失效。

X-W模型较EWK模型新颖之处在于:（1）提出了断裂包线的概念，从理论上更加清晰的揭示了损伤产生的机理;（2）在应用中强调了损伤对塑性变形历程中材料软化的耦合作用。但是X-W模型也存在以下几点不足:（1）与塑性过程耦合的损伤演化理论中涉及的无损伤状态下塑性变形时的本构曲线不能由试验得到，且从数学上很难准确构造，因而限制其工程应用的范围;（2）损伤累积公式中出现的参数m是由Manson-Coffin公式和Palmgren-Mines准则确定的，然而Manson-Coffin公式和 Palmgren-Mines准则是针对疲劳断裂提出的，所以参数m的确定不能很好地得到理论与实验的支持。

1.3 改进的三应力不变量延性断裂模型

上述两种模型的损伤公式中均体现了第一主应力不变量I1、第二偏应力不变量J2和第三偏应力不变量J3对损伤变量D的影响。因而，这两种模型的一般表达式也可写为如下形式:

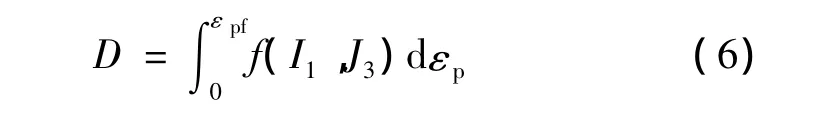
其中f为第一主应力不变量I1和第三偏应力不变量J3某种形式的函数;εp表示等效塑性应变;εpf表示断裂发生时材料点的等效塑性应变。其中εp反映了第二偏应力不变量J2的影响。结合EWK和X-W两种延性断裂模型的各自特点，同时采用EWK模型中的损伤与塑性过程非耦合的损伤累积理论提出了一种同样基于三应力不变量的延性断裂模型。

改进的三应力不变量延性断裂模型依据X-W模型的断裂包线形式，其中综合考虑到静水压力和Lode角的影响。其断裂包线εf表达式定义为:

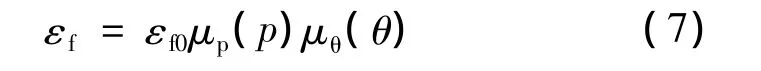
在表达式（7）中εf0为静水压力p为零时的断裂应变 ，μp（p）为静水压力p的函数，μθ（θ）为 Lode角θ的函数，其表达式为:

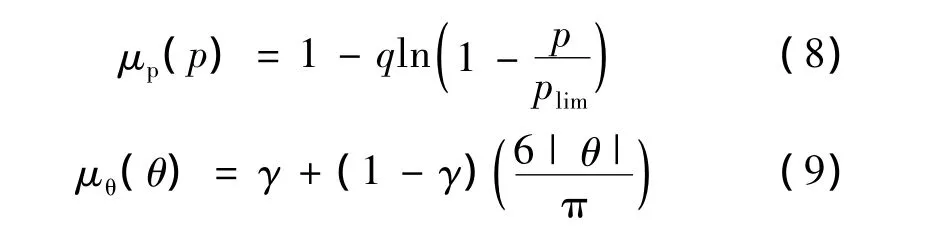
式（8）中q和式（9）中γ均为材料常数，式（9）中Lode角θ一般用来判定结构中某一点的偏应力状态，其表达式如下:

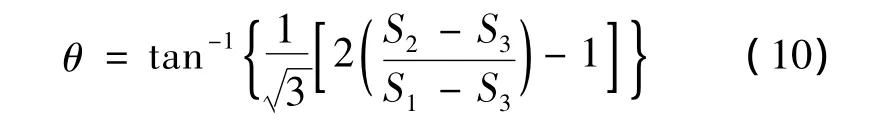
其中，S1，S2，S3为递减顺序的三个主偏应力。

改进的三应力不变量延性断裂模型采用线性损伤演化方程如下:

式（11）相应的微分形式为:

损伤的累积就可以表达为如下的积分形式:

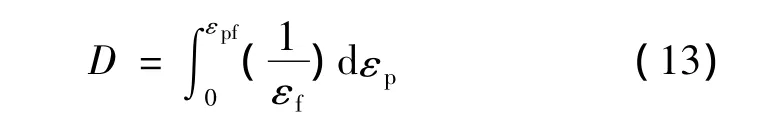
其中D为损伤变量，εp为等效塑性应变，εf为断裂包线。式（13）中，当 εp=0时，D=0，材料点无损伤。当εp=εpf时，D=1，材料点失效。由式（7）至式（13）可得改进的三应力不变量延性断裂模型的表达式如下:

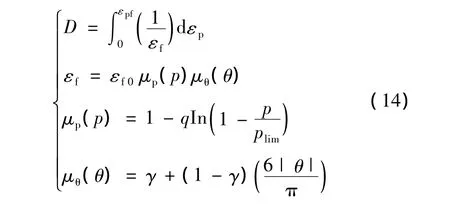
D=0，材料点无损伤。D=1，材料点失效。该改进的三应力不变量延性断裂模型的优点在于保留了X-W断裂模型的断裂包线的表达形式，同时采用EWK模型中的损伤与塑性过程非耦合的损伤累积理论，便于工程应用。

2 金属板构件拉伸试验

金属构件单向拉伸试验所选材料为高强度变形铝合金2A12-T4。该合金具有良好的塑性成型能力和机械加工性能，能够获得各种类型的制品。因此2A12-T4在航空工业中得到了广泛应用，其主要化学成分见表1。

四种金属构件试验分别为:两种不同厚度的光滑板材拉伸试验（试件a和b），两种不同厚度的带有中心孔板拉伸试验（试件c和试件d），试验依据为HB5143-96。四种金属构件的拉伸试验均在Instron8801试验机上进行。试验件尺寸见表2，图1。4种试件断裂时裂纹扩展形貌见图2。由试验所得两种不同厚度光滑板材的工程应力-工程应变曲线见图3。

表1 铝合金2A12-T4的化学成分（质量分数/%）Table 1 Chemical compositions of 2A12-T4（mass fraction/%）

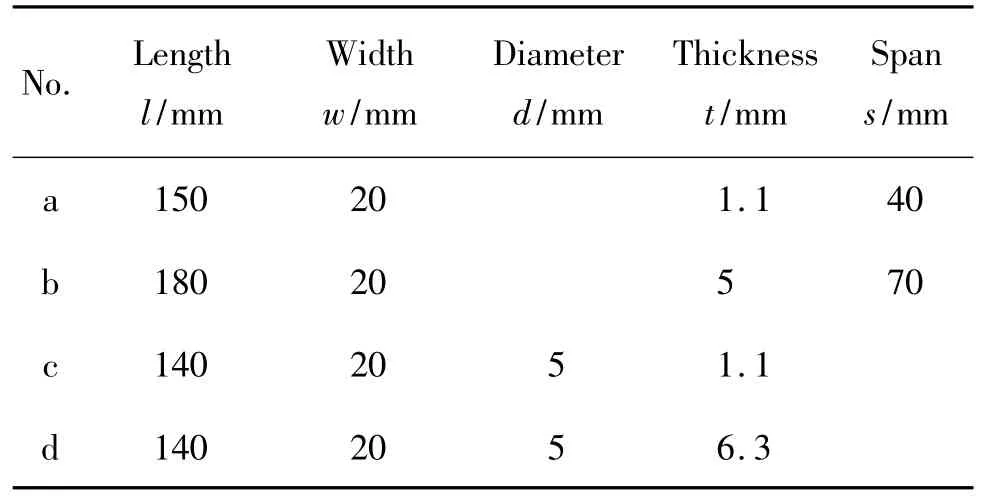
表2 四种试验件尺寸Table 2 Geometry of four specimens

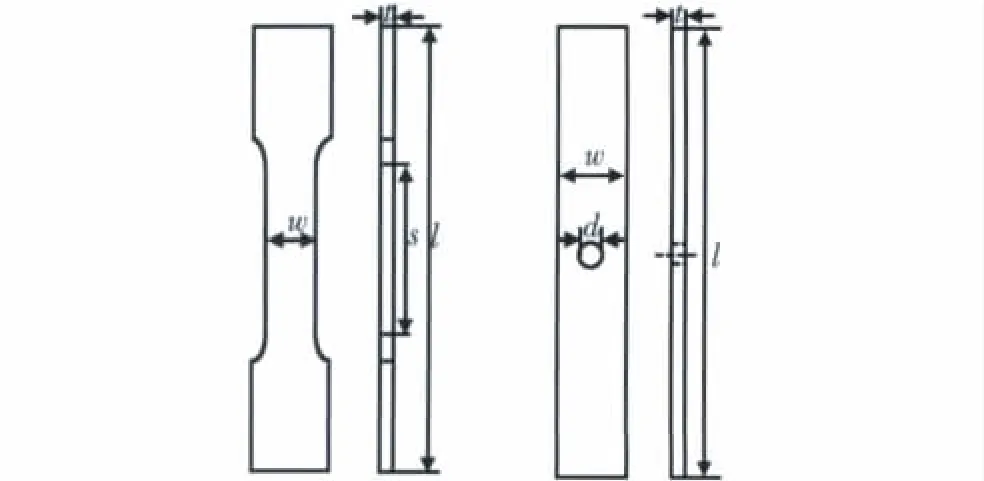
图1 试验件尺寸Fig.1 Geometry of specimens

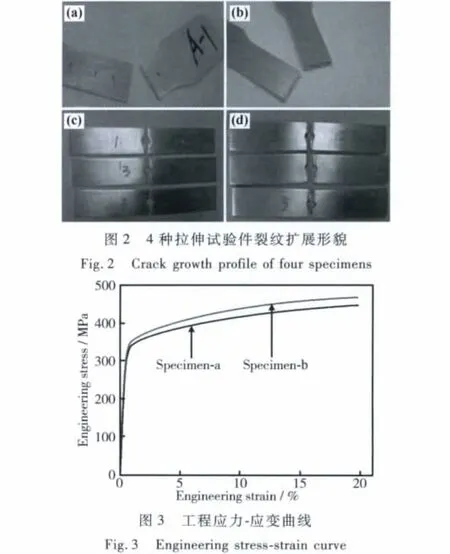
由图3所示曲线发现:不同厚度的光滑板材虽然均为标准试件，且材料相同但是由试验得出的应力应变曲线却并非相同。薄板材的屈服应力和屈服极限均小于较厚板材的对应值，通过查阅相关材料试验手册［14］也发现了同样的现象。从工程应用的角度出发，选择薄板材的应力-应变曲线是相对安全的。但是从科学研究和有限元仿真的角度出发，本文对光滑薄板（试件a）和厚度t=1.1mm带有中心孔板（试件c）因其厚度相同而选择试件a单向拉伸所得试验结果，对厚度t=5mm光滑板材（试件b）和厚度t=6.3mm带有中心孔板（试件d）因其厚度接近而选择试件b单向拉伸所得的试验结果进行数值计算。

3 金属板构件拉伸试验数值计算

3.1 三维有限元模型和算法流程

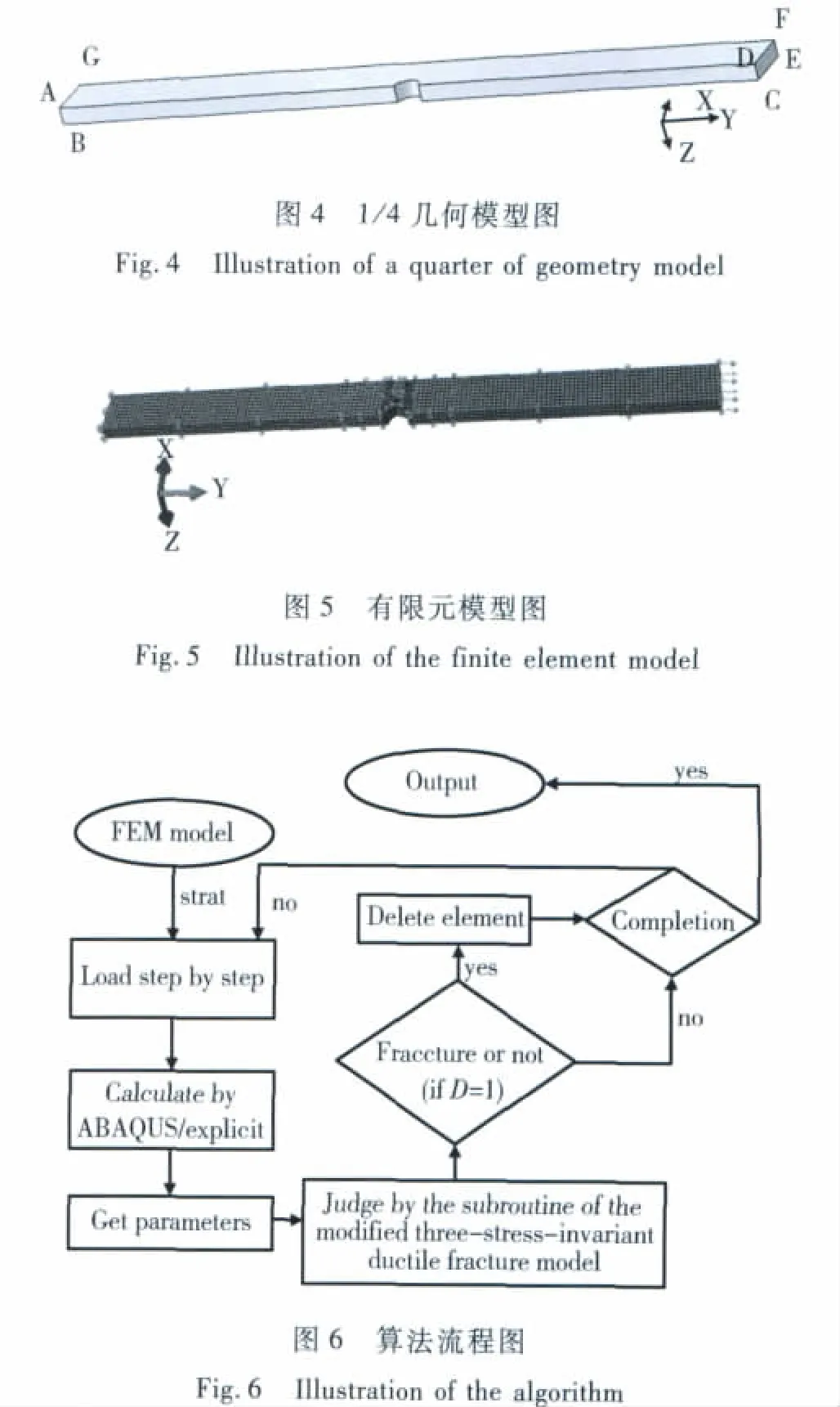
由于四种金属板材试验件及载荷在厚度方向（z方向），宽度方向（x方向）和长度方向（y方向）对称。为了更直观的将有限元仿真结果与试验结果对比分析，以试件d为例，有限元模型选择真实试件的1/4，分别沿厚度方向（z方向）取一半，宽度方向（x方向）取一半。如图4，图5所示，在厚度方向（其对称面为ADFG面，z=0）和宽度方向（其对称面为ABCD面，x=0）的对称面上施加对称约束，长度方向（y方向）一端施加位移约束，另一端添加位移载荷（沿y正方向垂直于面CEFD）。划分网格时两端稀疏，孔边危险区域加密，最小单元尺寸选择肉眼可直接观测的最小裂纹长度等于0.1mm，单元类型采用缩。减积分体单元（C3D8R）。为了验证改进的三应力不变量延性金属断裂模型的有效性，通过编写用户材料子程序VUMAT的方式将该延性金属断裂模型嵌入ABAQUS准静态算法主程序来模拟金属板材试件的整个断裂过程［15］。有限元数值计算所选材料弹性模量E=71200MPa，密度ρ=2700kg/m3，泊松比 μ =0.33，材料常数 εf0=0.35，q=1000，γ=0.25，plim=0.55。总体算法的实现是建立在对有限单元积分点进行计算的基础上。商业有限元软件ABAQUS/explicit准静态算法主程序对每个单元的每个积分点进行计算，在一个增量步之内完成计算后，VUMAT子程序将主程序得到的该断裂模型所需参数进行提取，通过子程序计算出损伤变量D，若损伤变量D达到断裂阀值1，通过内部变量传递至主程序令该单元失效。否则不做任何变化，遍历所有单元积分点进行判断后，程序进入下一增量步计算。整个加载过程的若干增量步中主程序与子程序之间实时进行通信。载荷施加完毕时输出最终结果，算法流程图如图6所示。本算法最终断裂在单元上发生，通过删除单元来模拟裂纹扩展，直至构件完全断裂。

3.2 试验数据与有限元仿真结果对比分析

数值计算中考虑延性金属有限变形的弹塑性效应（物理非线性）和几何非线性效应通过编写用户材料子程序VUMAT将改进的三应力不变量延性断裂模型嵌入ABAQUS非线性有限元显式算法主程序，选用位移加载的方式单向拉伸四种高强度变形铝合金2A12-T4板材试件直至断裂。

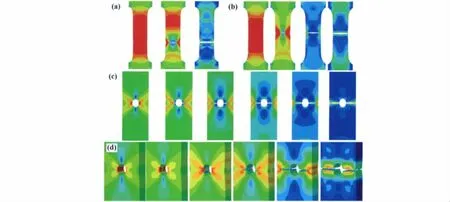
图7 4种试件裂纹扩展 （a）试样a;（b）试样b;（c）试样c;（d）试样d;Fig.7 Crack propagation of four specimens（a）speciment-a;（b）speciment-b;（c）speciment-c;（d）speciment-d;

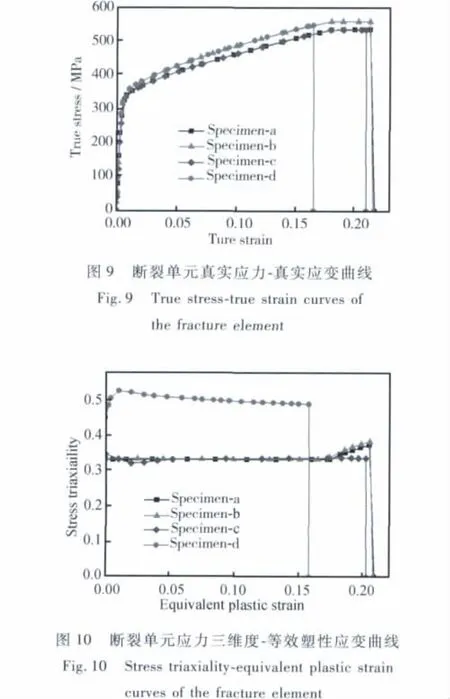
在ABAQUS后处理中应用对称显示分析结果的方式对1/4几何模型分析结果进行全尺寸模型结果显示，改进的三应力不变量延性断裂模型进行的数值计算所得裂纹从萌生和扩展直至完全断裂过程见图7。从图7可知在宽度方向上光滑板材裂纹均从其中心处开始萌生然后向边缘开始扩展直至断裂，带孔板的裂纹沿孔边的中心处开始萌生并向边缘扩展。在厚度方向上裂纹先从模型的厚度中心处开始萌生，然后向板的厚度和宽度边缘扩展。将数值仿真中裂纹扩展形貌与图2中真实试件的裂纹扩展形貌对比，数值计算结果较好地反映了真实试验的断裂过程，数值仿真所得裂纹扩展形貌和裂纹扩展路径与真实实验结果基本一致。由单向拉伸试验所得4组载荷-位移曲线与有限元数值计算所得载荷-位移曲线对比见图8。从图8中4种板材试件的载荷-位移曲线对比中发现，仿真结果较好地预测了真实试验的载荷-位移曲线。在数值计算对四种板材试件的宏观载荷-位移曲线进行较好预测的基础上，在ABAQUS软件后处理分析的结果中提取了有限元模型的最先断裂单元的真实应力-应变曲线（如图9所示）和断裂单元的应力三维度-等效塑性应变曲线（如图10所示）进一步对微小单元进行了探讨。从图9所示曲线可知:两种不同厚度的光滑无孔板材（试件a和试件b）断裂发生时单元应变基本一致，而两种不同厚度的带有中心孔的板材试件（试件c和试件d）在断裂发生时单元应变相差较大。图10通过对断裂单元应力三维度与等效塑性应变的关系解释了上述差异的原因:应力三维度对断裂发生时单元应变影响显著，随着应力三维度的增大，断裂发生时单元的等效塑性应变减小，因而单元的真实应变也减小。图10也反映出应力三维度与构件的几何形状具有密切相关性:两种不同厚度的光滑无孔板材（试件a和试件b）随着厚度的增加断裂单元处应力三维度变化不明显，断裂发生时单元应变也相近。而两种不同厚度的带有中心孔的板材试件（试件c和试件d）随着厚度的增加，在三向应力作用下断裂单元处应力三维度相差明显，因而断裂发生时单元应变也相差明显。

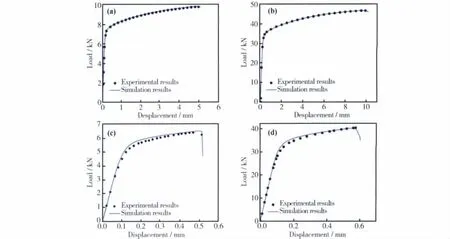
图8 对比载荷-位移曲线的试验数据和仿真结果Fig.8 Comparisons of load-displacement curves between experimental and simulation results:（a）specimen-a;（b）specimen-b;（c）specimen-c;（d）specimen-d

4 结论

（1）通过分析EWK和X-W两种金属延性断裂模型，结合两种断裂模型的各自特点提出了一个改进的三应力不变量延性金属断裂模型，并将其应用于金属板材的静强度渐进破坏过程预测。

（2）使用改进的三应力不变量延性金属断裂模型很好地预测了4种无初始裂纹缺陷的高强度变形铝合金2A12-T4板材试件在静强度渐进破坏时裂纹的萌生，扩展直至完全断裂的全过程。

（3）改进的三应力不变量延性金属断裂模型很好地预测了4种铝合金板材试件的载荷-位移曲线，准确地预测了断裂时的载荷，较好地反映了延性金属材料的断裂过程。

［1］TAIRA S，TANAKA K.Thickness effect of notched metal sheets on deformation and fracture under tension［J］.Engineering Fracture Mechanics，1979，11（2）:231-249.

［2］PARDOEN T，MARCHAL Y，DELANNAY F.Thickness dependence of cracking resistance in thin aluminum plates［J］.Journal of the Mechanics and Physics of Solids，1999，47（10）:2093-2123.

［3］PARDOEN T，MARCHAL Y，DELANNAY F.Essential work of fracture compared to fracture mechanics-towards a thickness independent plane stress toughness［J］.Engineering Fracture Mechanics，2002，69（5）:617-631.

［4］JOHNSON G R，COOK W H.Fracture characteristics of three metals subjected to various strains，strain rate，temperatures and pressures［J］.Engineering Fracture Mechanics，1985，21（1）:31-48.

［5］岳珠峰，张克实，郑长卿.不同应力三维度下空穴膨胀的模拟计算与分析［J］.航空学报，1992，13（11）:698-701.

（YUE Z F，ZHANG K S，ZHENG C Q.The computer simulation and analysis of void growth in different stress triaxialities［J］.Acta Aeronautica et Astronautica Sinica，1992，13（11）:698-701.

［6］RICE J R，TRACEY D M.On the ductile enlargement of voids in triaxial stress fields［J］.Journal of the Mechanics and Physics of Solids，1969，17（3）:201-217.

［7］GURSON A L.Continuum theory of ductile rupture by void nucleation and growth［J］.Journal of Engineering Materials and Technology，1977，99（1）:2-15.

［8］WANG T J.A continuum damage model for ductile fracture of weld heat affected zone［J］.Engineering Fracture Me-chanics，1991，40（6）:1075-1082.

［9］WANG T J.Micro-and macroscopic damage and fracture behavior of welding coarse grained heat affected zoned of a low alloy steel mechanisms and modeling［J］.Engineering Fracture Mechanics，1993，45（6）:799-812.

［10］KAMOULAKOS A，CULIERE P，ARAKI T.Prediction of ductile metal rupture with the E-W Model in PAMCRASH:Proceedings of the international body engineering conference，Chiba，Japan［C］.Tokyo:Society of Automotive Engineers of Japan，2003:47-52.

［11］KAMOULAKOS A.The ESI-Wilkins-Kamoulakos rupture model［M］//RAABE D ，ROTERS F，CHEN L Q，et al.Continuum Scale Simulation of Engineering Materials:Fundamentals-Microstructures-Process Applications，Weinheim:Wiley-VCH Verlag GmbH ＆ Co.KGaA，2004:795-804.

［12］XUE L.Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading ［J］.International Journal of Solids and Structures，2007，44（16）:5163-5181.

［13］杨锋平，孙秦.韧性金属材料渐进断裂的有限元算法研究［J］. 金属学报，2008，44（4）:489-494.

（YANG F P，SUN Q.Algorithm Study of Gradual of Fracture of Ductile Metallic Material with Finite Element Method［J］.Acta Metall Sinica，2008，44（4）:489-494.

［14］颜鸣皋，刘伯操，李金桂，等.中国航空材料手册（第三卷）［M］.北京:中国标准出版社，2002.

［15］庄茁，由小川，廖剑晖等.基于ABAQUS的有限元分析和应用［M］.北京:清华大学出版社，2009.