基于非线性反应谱法的小箱梁桥延性抗震设计方法

易祥军

(海南省交通规划勘察设计研究院， 海南 海口 570206)

0 引言

地震激起的惯性力较大，对于普通结构，若单纯依靠强度来抵抗地震，将造成巨大的材料浪费。目前，包括我国在内的大多数国家都已经将“小震不坏，大震不倒”的二阶段设计方法作为基本设防思想[1]：中小震作用下，要求结构处于弹性状态，以强度破坏为准则；而强震作用下，结构可发生一定的塑性变形和有限损伤，以延性破坏为准则。Newmark等[2]在提出延性概念的同时，也提出了非线性反应谱，即在按反应谱理论计算地震响应时，考虑塑性变形影响，对线形反应谱进行修正，用等效线性化方法来考虑结构的非线性特性。

1 延性指标选取

延性抗震理论与强度理论不同之处在于，它通过结构选定部位(称为塑性铰)的塑性变形来抵抗地震作用。利用塑性铰，能消耗地震能量、延长地震周期、减小地震反应。

对于各类延性指标的定义如下。

1.1 位移延性系数[3]

位移延性系数为构件的极限位移与屈服位移之比：UΔ=Δu/Δy。

1.2 塑性铰位置选择

对于延性构件，潜在塑性铰位置的选择主要有两个原则： ① 使结构获得最优的耗能；②易于发现和修复。本文选取30 m跨径的小箱梁进行分析，把桥墩作为延性构件，顺桥向墩身弯矩分布为倒三角，并在墩底设铰；横桥向由于盖梁约束，墩顶和墩底弯矩大小不确定，应在墩顶和墩底均设铰。

1.3 地震强度折减系数

一般结构延性水平分为完全延性结构、有限延性结构和完全弹性结构和可利用的位移延性水平越高，地震力的折减系数越大。图1近似表达了可利用的延性与地震力的对应关系。

图1 位移延性系数与地震力对应关系

地震力强度折减系数Ru，定义为单自由度弹性系统最大地震惯性力FE与相应延性系统的屈服力Fy之比，即：

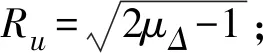
μΔ与延性类型的关系，参考了Paulay[4]的理论，其研究表明有限延性结构允许的位移延性系数通常为1.5～3.5，完全延性结构允许的位移延性系数通常为3.5～8。过低的容许值会增加结构的造价，但过高的容许值可能偏于不安全。各国规定的位移延性系数容许值一般不超过6，本文在区间内取多个值作为μΔ，并进行对比。

1.4 非线性反应谱的建立

根据本研究桥梁所在地区抗震资料，由规范[5]得到E2地震下线性加速度反应谱(E1地震作用下结构须处于弹性阶段，不予考虑)，进行折减即得到非线性反应谱，如图2所示。

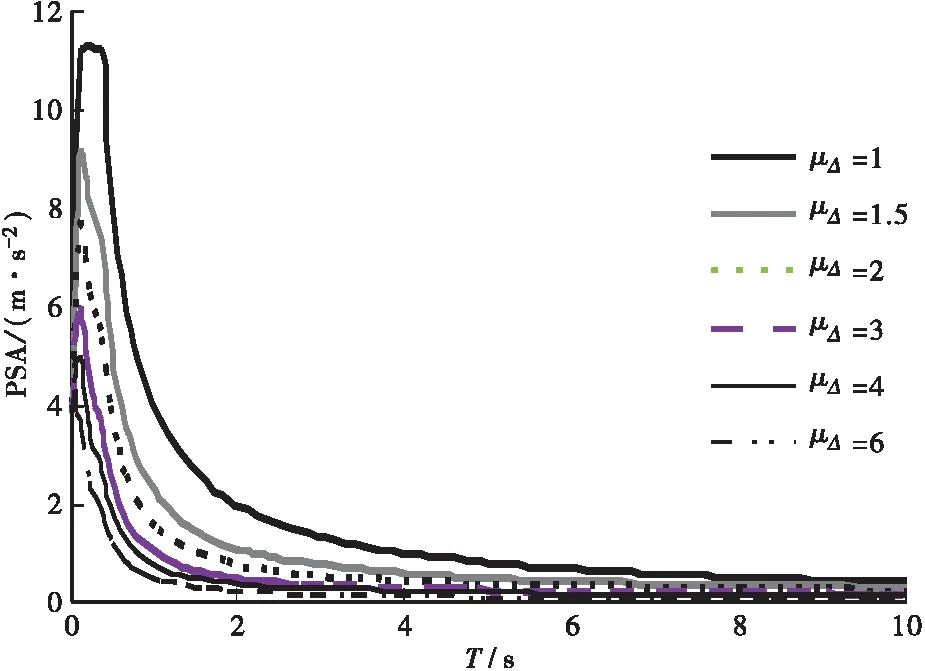
图2 线形反应谱与折减后的非线性反应谱

反应谱曲线总是在周期T=0.1 s时达到峰值，表1给出各μΔ对应的峰值点折减系数Rμ。由表1可知，随着μΔ的增长峰值点折减逐渐增多。

表1 各对应加速度谱峰值点折减系数μΔRμ(0.1 s, μΔ)μΔRμ(0.1 s, μΔ)1.01.03.01.81.51.24.02.22.01.46.03.0

2 基于非线性反应谱法的小箱梁桥设计

2.1 工程概况

南渡江大桥位于海南省澄迈县永发镇，跨越南渡江，大桥上部结构采用7×(5×30 m)先简支后连续预应力混凝土箱梁，梁高1.6 m；桥墩采用柱式桥墩，墩的直径均为1.6 m，桩的直径为1.8 m。桥型布置见图3。

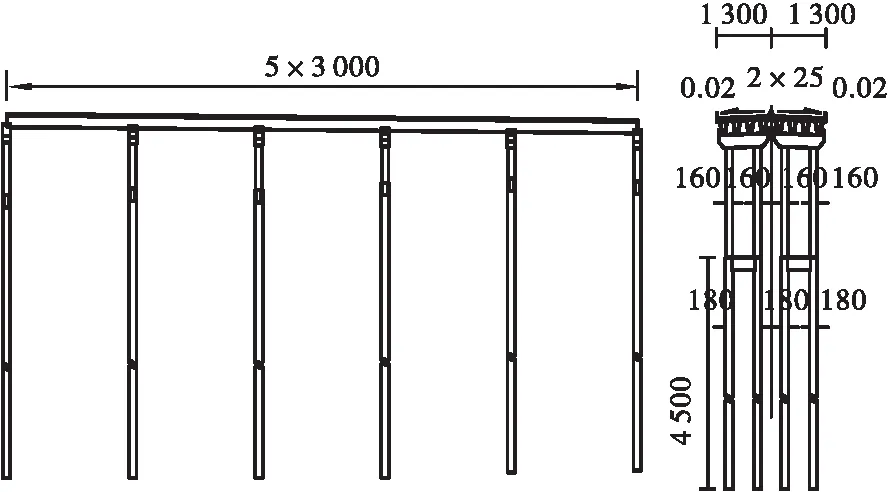
图3 南渡江大桥连续箱梁桥型布置图(一联)(单位： cm)

采用MIDAS/CIVIL有限元软件对桥梁进行分析,采用梁格模型建模。本桥抗震设防类别为B类，设防烈度为8度，水平向设计基本地震动加速度峰值为0.30 g，场地类别为Ⅱ类，设计加速度反应谱特征周期为0.35 s。

取7联中墩高最矮的一联作为算例，墩高如表2。

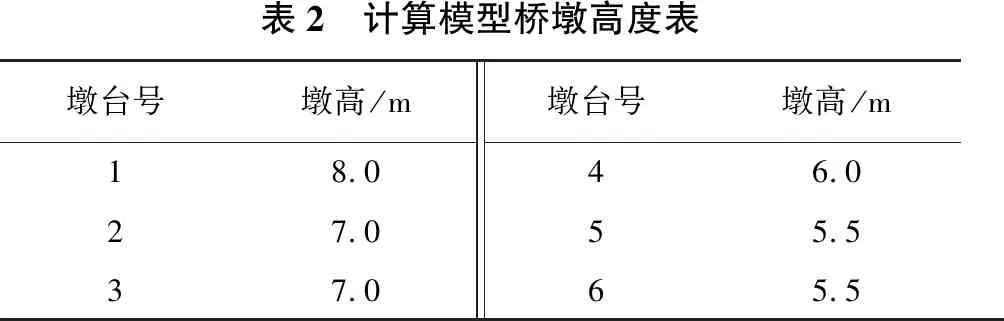
表2 计算模型桥墩高度表墩台号墩高/m墩台号墩高/m18.046.027.055.537.065.5

2.2 非线性反应谱结构响应

采用CQC法进行振型组合，计算模型如图4。图5和图6分别给出了顺桥向和横桥向反应谱作用下弯矩分布，由图可见，地震主要影响部位是墩柱和桩基，对上部结构影响很小。

桥墩在各反应谱作用下主要截面弯矩如表3、表4所示。归纳出采用不同位移延性系数对地震响应的折减程度，见表5。

图4 计算模型

图5 顺桥向地震反应谱作用下全桥弯矩分布

图6 横桥向地震反应谱作用下全桥弯矩分布

表3 顺桥向反应谱作用下桥墩主要截面弯矩对比弯矩输出位置墩号μΔ=1μΔ=1.5μΔ=2μΔ=3μΔ=4μΔ=6墩底1#7 607.594 252.312 990.641 912.551 424.37958.055#6 551.373 733.202 654.791 717.651 286.94871.01

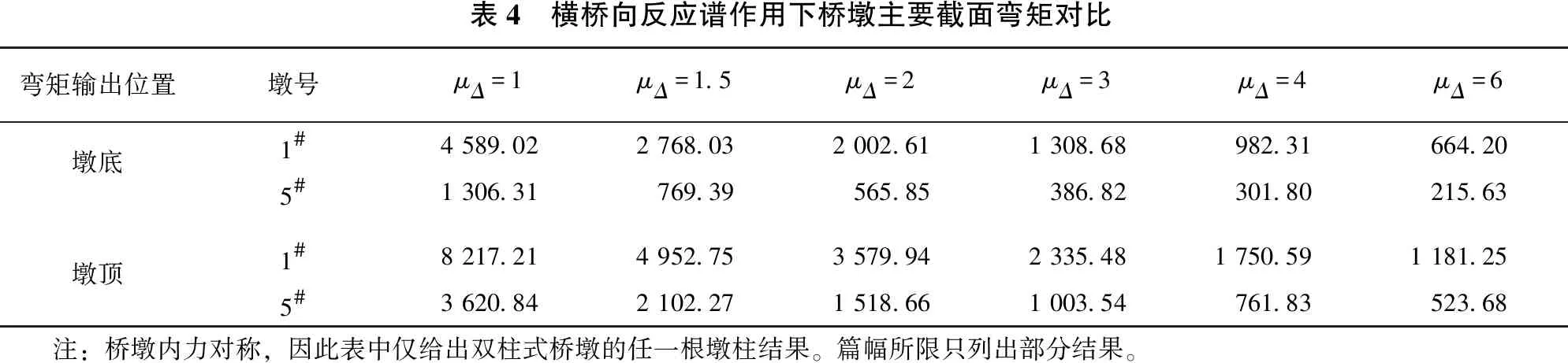
表4 横桥向反应谱作用下桥墩主要截面弯矩对比弯矩输出位置墩号μΔ=1μΔ=1.5μΔ=2μΔ=3μΔ=4μΔ=6墩底1#4 589.022 768.032 002.611 308.68982.31664.205#1 306.31769.39565.85386.82301.80215.63墩顶1#8 217.214 952.753 579.942 335.481 750.591 181.255#3 620.842 102.271 518.661 003.54761.83523.68 注:桥墩内力对称,因此表中仅给出双柱式桥墩的任一根墩柱结果。篇幅所限只列出部分结果。

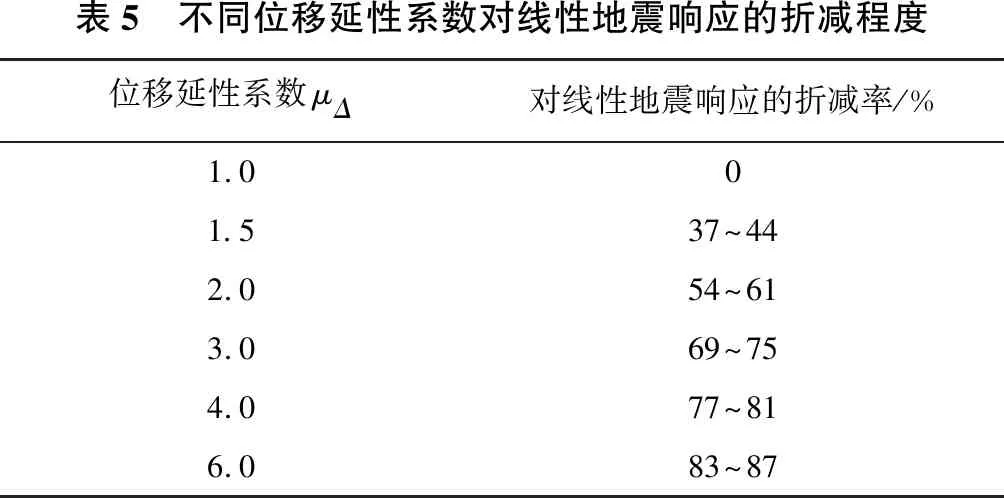
表5 不同位移延性系数对线性地震响应的折减程度位移延性系数μΔ对线性地震响应的折减率/%1.001.537～442.054～613.069～754.077～816.083～87

2.3 塑性铰模拟

通过对纵筋配筋率、轴压比、配箍率3个参数开展分析，讨论参数取值对曲率延性的影响。从经济性和增强延性能力考虑，选取加密箍筋，采用螺旋箍筋的方法提高延性。

采用双折线模型，屈服点定义为钢筋发生初始屈服。例如对于3#墩底截面，轴压比13.8%、纵筋配筋率0.98%(40φ25)、配箍率0.63%(φ16@80)时，双折线模型如图7。

等效塑性铰长度按08抗震设计细则[5]计算。

图7 塑性铰截面双折线模型示例

2.4 位移延性系数分析

顺桥向和横桥向塑性铰区别在于屈服特性：顺桥向塑性铰轴力恒定，屈服强度一定；横桥向塑性铰需考虑轴力变化，用屈服面描述屈服强度。二者并无根本区别，后者仅在计算上较繁琐。本文以说明延性设计方法为主，仅以顺桥向为例进行全桥PUSHOVER分析。由于全桥推覆比单个桥墩推覆结果更准确，且3种侧向力分布模式的计算结果差别很小，按照全桥推覆方法，给出侧向力按照顺桥向基本振型分布时的结果。

位移延性系数通常定义为上部结构质心处的极限位移与屈服位移之比，取结构的屈服位移Δy为首次出现塑性铰屈服时的上部结构质心位移，取极限位移Δu为任一塑性铰达到极限点时的上部结构质心位移。图8给出各墩底截面弯矩随荷载步的变化情况(本计算模型共80个荷载步)。

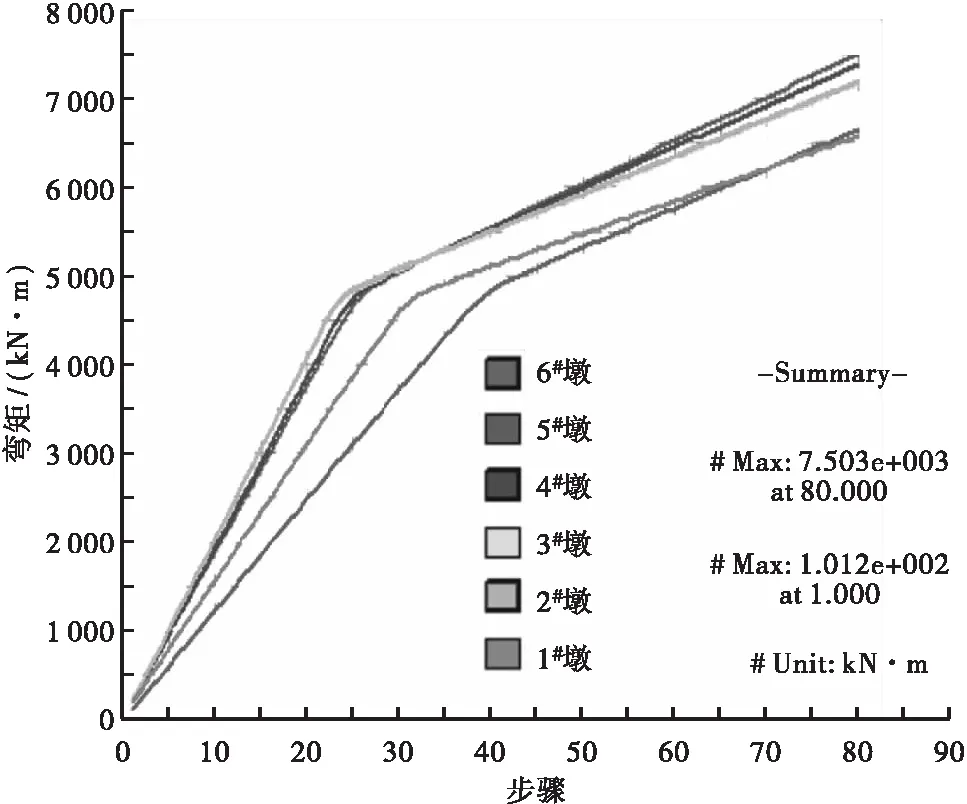
图8 各墩底截面弯矩

虽然上部结构位移延性系数并不大，但此时墩顶位移延性系数却为10左右，上部结构位移延性能力比桥墩小得多，说明支座附加柔度很大。其原理简单概括为：当不考虑支座柔度，上部结构位移延性系数与墩顶相同；如果支座柔度越大，上部结构极限位移也相应越大，墩顶屈服位移则相对显得越小，位移延性系数相应就越小。

考虑设定不同的位移延性系数，分别给出合适的纵筋配筋率和配箍率，结果如表6所示。此处“合适”指刚好满足抗弯强度、延性需求以及构造要求，且富余不大。

表6显示，当结构可利用的位移延性系数在2以上时，抗弯强度已不影响设计，纵筋按构造配置即可，可见考虑结构延性后，地震力的折减程度相当可观；当可利用的位移延性系数在2以下时，配箍率按照08抗震细则规定的构造要求即可满足延性要求，可见规范对箍筋的配置要求已经较高。此外，μΔ设定为3已经可以折减69%～75%的地震力(见表5)，折减程度相当可观。若μΔ取值更大，箍筋过密，配置将有一定困难。上表仅考虑结构延性需求，并未考虑规范对结构位移的规定。规范对塑性铰区转角和墩顶位移均给出了限值，还应进行相应验算。

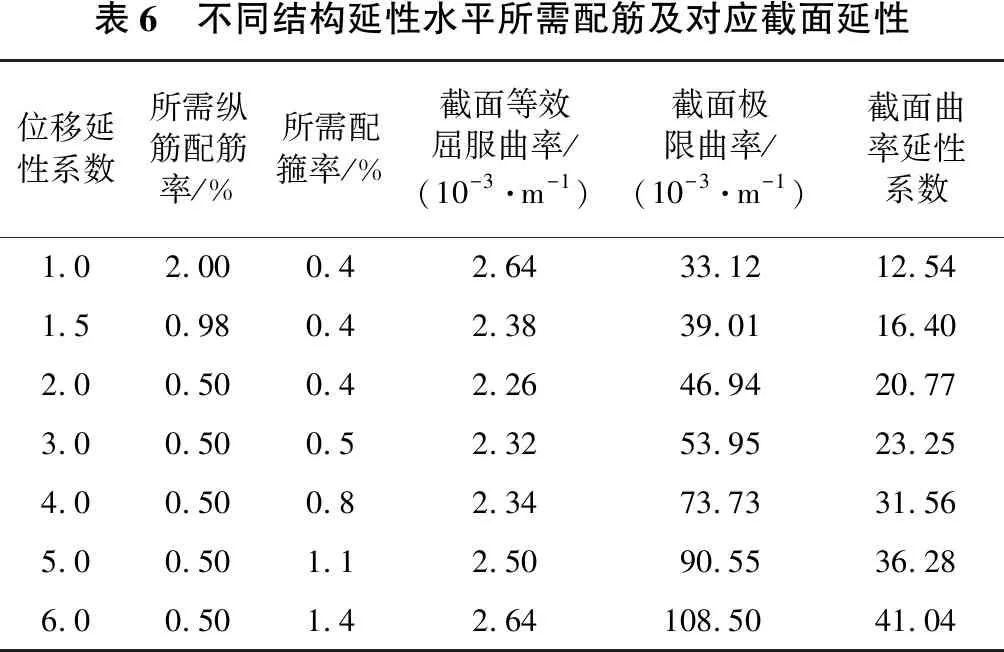
表6 不同结构延性水平所需配筋及对应截面延性位移延性系数所需纵筋配筋率/%所需配箍率/%截面等效屈服曲率/(10-3·m-1)截面极限曲率/(10-3·m-1)截面曲率延性系数1.02.000.42.6433.1212.541.50.980.42.3839.0116.402.00.500.42.2646.9420.773.00.500.52.3253.9523.254.00.500.82.3473.7331.565.00.501.12.5090.5536.286.00.501.42.64108.5041.04

2.5 结构位移的检算

经试算，顺桥向地震作用下，本桥较为合适的结构位移延性系数为1.5，钢筋配置为：配筋率0.98%(40φ25)、配箍率0.63%(φ16@80)。此时各桥墩抗弯强度安全系数最小为1.4。

反应谱法计算结构位移，只能给出结构弹性响应结果，通过调整系数近似得到结构实际位移。当然，此时必须采用弹性反应谱，而不能使用折减后的非线性反应谱。国内外大量研究表明：当结构的自振周期大于反应谱的特征周期，对于规则桥梁适用等位移原则，即对于同样边界条件，地震作用下，按弹性分析与弹塑性分析得出的位移近似相等。只有当结构的自振周期较短时，采用等位移原则得到的位移偏小，才需要修正。同济大学参考国外研究成果，通过大量参数分析，建议如下相关修正系数：结构自振周期小于0.1 s时，调整系数取1.5；结构自振周期大于反应谱特征周期时，调整系数取1.0；其间按线性插值计算调整系数。

反应谱计算结构响应，一般采用振型分解法。按照上述原则，对于各振型需要分别给出调整系数，具体可在振型组合时人为修正振型组合系数。对于本桥，从第14振型开始需要进行修正。

按照08抗震设计细则，各墩塑性铰区转角位移θp检算结果如表7所示。各墩底塑性铰区转角位移安全系数最小为7.91，在满足规范要求的基础上富余很大。

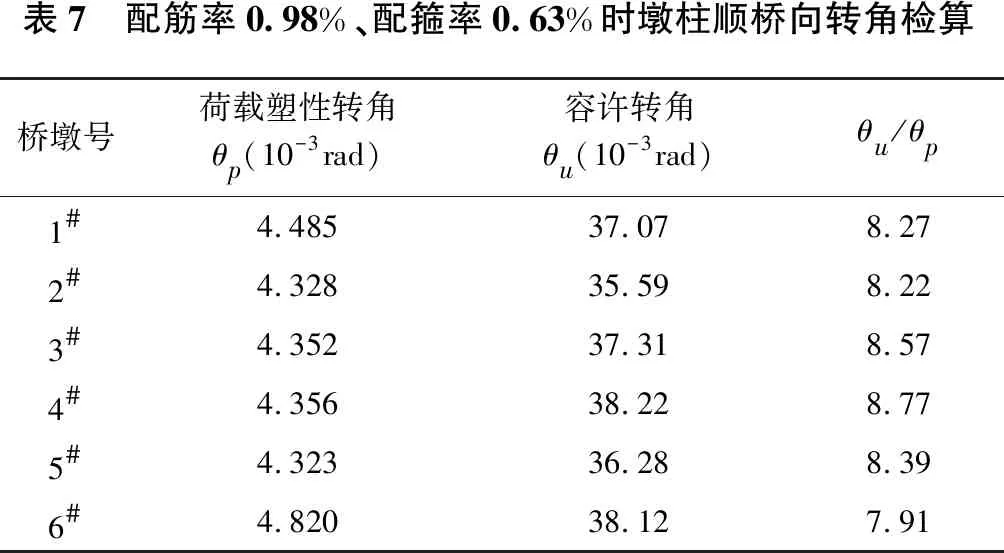
表7 配筋率0.98%、配箍率0.63%时墩柱顺桥向转角检算桥墩号荷载塑性转角θp(10-3rad)容许转角θu(10-3rad)θu/θp1#4.48537.078.27 2#4.32835.598.22 3#4.35237.318.57 4#4.35638.228.77 5#4.32336.288.39 6#4.82038.127.91

按照08抗震设计细则还需检算墩顶位移。同样根据根据PUSHOVER分析得到结构的极限位移，即容许位移值Δu。检算结果如表8所示，墩顶位移安全系数为3.26，说明结构整体为安全。

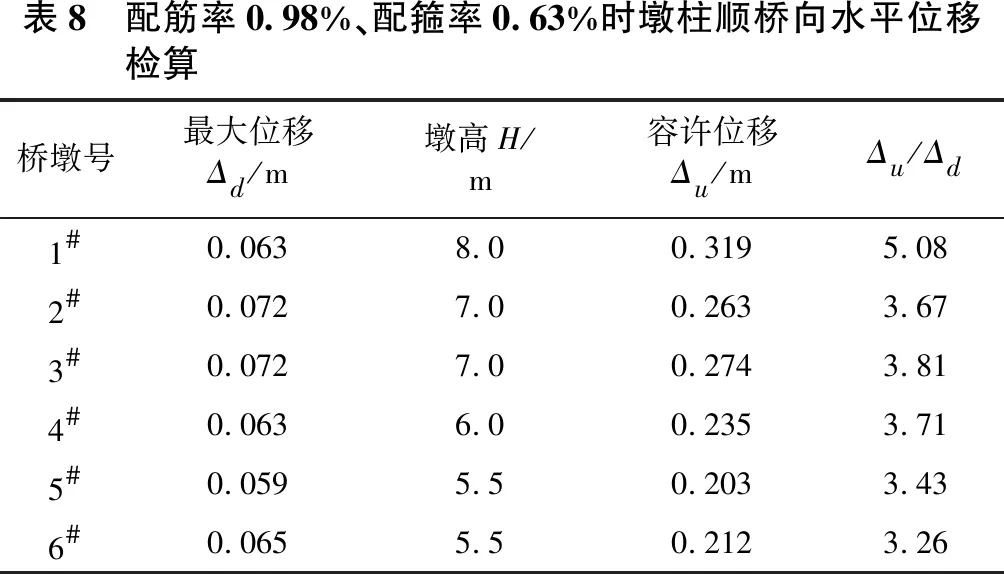
表8 配筋率0.98%、配箍率0.63%时墩柱顺桥向水平位移检算桥墩号最大位移Δd/m墩高H/m容许位移Δu/mΔu/Δd1#0.0638.00.3195.082#0.0727.00.2633.673#0.0727.00.2743.814#0.0636.00.2353.715#0.0595.50.2033.436#0.0655.50.2123.26

总的来说，延性设计最好的做法是针对各延性水平均进行试算，通过比选得到经济性和安全性俱佳的位移延性水平。

3 结论

1) 考虑了结构位移延性后，地震力能得到很大折减。原则上结构的位移延性系烽可取1～6之间，但当支座附加柔度较大时，例如采用板式橡胶支座的情况下，本文建议结构位移延性系数取值不宜超过3。

2)塑性铰模拟时，一般将实际截面弯矩 — 曲率关系转化为双折线或三折线模型。

3)影响曲率延性的因素中，对延性能力影响较为显著的是箍筋配置，配箍率增大可使延性能力显著提高。

4)由PUSHOVER分析得到结构位移延性的方法。进行了全桥PUSHOVER分析，提出了全桥结构PUSHOVER分析中屈服点和极限点的判定方法。