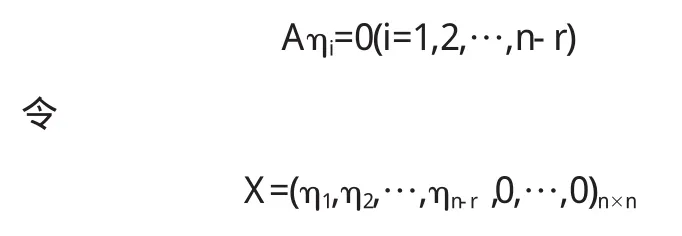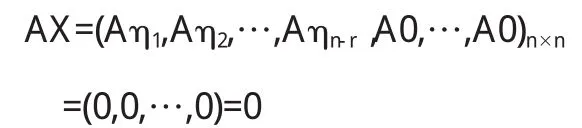方阵的零因子

林大华

（闽江学院数学系，福建福州350108）

方阵的零因子

林大华

（闽江学院数学系，福建福州350108）

给出方阵零因子的概念，讨论了方阵零因子的性质，及方阵存在零因子的条件，得到了若干结论，并用方阵零因子刻画了矩阵理论中的若干结论.

方阵；零因子；性质

1 预备知识

本文用Pn×n既表示数域P上n方阵关于矩阵的加法与数乘运算构成的线性空间，也表示数域P上n方阵关于矩阵的加法与乘法运算构成的矩阵环.用分别表示矩阵A的共轭矩阵，转置矩阵，伴随矩阵，秩.其它记号可参见文献[1].

定理1-1设A，B∈Pn×n，则

1）AB=AB；

2）(AB)T=BTAT；

3）(AB)*=B*A*

定义1-1设A，X∈Pn×n则

1）当XA=0时，称X是A的左零因子；

2）当AX=0时，称X是A的右零因子；

3）当X既是A的左零因子，又是A的右零因子时，称X是A的零因子.

显然，n阶零矩阵是所有n阶方阵的零因子.方阵A的零矩阵以外的零因子（如果有的话），称为A的非零零因子.

另外，所有n方阵都是A的左（右）零因子⇔A是零矩阵.

注：A的左（右）零因子未必是A的右（左）零因子.

2 主要结论

定理2-1若X,Y是A∈Pn×n的左（右）零因子，则

1）kX+lY也是A的左（右）零因子，其中k,l是数域P中任意数；

2）XY也是A的左（右）零因子；

3）Xm也是A的左（右）零因子，其中m是正整数；

4）XT是AT的右（左）零因子；

5）X*是A*的右（左）零因子；

6)∀B∈Pn×n,BX(XB)仍是A的左（右）零因子.

证明若X,Y是A的左零因子，则XA=0,YA=0.

1）因为(kX+lY)A=k(XA)+l(YA)=k0+l0=0，所以kX+lY也是A的左零因子.

2）因为(XY)A=X(YA)=X0=0，所以XY也是A的左零因子.

3）因为XmA=Xm-1(XA)=Xm-10=0，所以Xm也是A的左零因子.

4）因为ATXT=(XA)T=0T=0，所以XT是AT的右零因子.

5）因为A*X*=(XA)*=0*=0，所以X*是A*的右零因子.

6）因为(BX)A=B(XA)=B0=0，所以BX是A的左零因子.

同理可证X,Y是A的右零因子时，结论也成立.

由定理2-1可知若A∈Pn×n有左（右）非零零因子，则A一定有无穷多个左（右）零因子，而且有下列推论.

推论2-2矩阵A∈Pn×n的所有左（右）零因子集合，构成线性空间Pn×n的子空间.

推论2-3矩阵A∈Pn×n的所有左（右）零因子集合，构成矩阵环Pn×n的左（右）理想.

定理2-4设A∈Pn×n，则A有非零左（右）零因子⇔r (A)

证明（⇒）设X是A的非零左零因子，则XA=0.若r (A)=n，则A可逆，于是有X=X(AA-1)=(XA)A-=0A-1=0，这与X是非零矩阵矛盾，故r(A)

同理可证，A有非零右零因子时，必要性也成立.

（⇐）因为r(AT)=r(A)

是非零矩阵，且ATX=0，从而XTA=0，即A有非零左零因子XT.

同理可证，A有非零右零因子.

定理2-5设Z，X∈Pn×n，则

1）X是A的右零因子⇔X的列向量是线性方程组Ax=0的解；

2）X是A的左零因子⇔X的行向量是线性方程组ATx=0的解；

证明1）设X(x1,x2,…,xn)，其中xi(i=1,2,…,n)是X的第i列.则AX=0⇔Axi=0⇔xi(i=1,2,…,n)是Ax=0的解.

2）因为XA=0⇔ATXT=0⇔XT的列向量是ATx=0的解⇔X的行向量是ATx=0的解.

推论2-6设A,X∈Pn×n，若X是A的左（右）零因子，则

证明若X是A的右零因子，则由定理2-5可知，X的列向量是线性方程组Ax=0的解，所以X的列向量可由线性方程组Ax=0的基础解系线性表示，于是X的列向量组的秩小于等于线性方程组Ax=0的基础解系所含向量的个数n-r (A)，即r(X)≤n-r(A)，故r(A)+r(X)≤n.

若X是A的左零因子，则由定理2-1可知，XT是AT的右零因子，于是有r(AT)+r(XT)≤n，又r(AT)=r(A)，r(XT)=r(X)，故r (A)+r(X)≤n.

定理2-7设A∈Pn×n，则r(A)=r

证明（⇒）因为r(A)=r

则r(X)=n-r，且

故X是A的秩为n-r的右零因子.

（⇐）设Y是A的秩为n-r的右零因子，则有AY=0，于是Y的列向量是线性方程组Ax=0的解.因为Y的秩为n-r，所以Y的列向量不全为零，从而Ax=0有非零解，故r(A) =r

定理2-8设A∈Pn×n，则

1）A无非零左零因子⇔A无非零右零因子；

2）A无非零左零因子⇔∀X，X∈Pn×n，当XA=YA时，有X=Y；

3）A无非零右零因子⇔∀X，X∈Pn×n，当AX=AY时，有X=Y.

证明1）由定理2-3可知，A无非零左零因子⇔r(A)=n⇔A无非零右零因子.

2）（⇒）当XA=YA时，有(X-Y)A=0，因为A无非零左零因子，所以有X-Y=0，故X=Y.

（⇐）若A有非零左零因子X，则有XA=0=0A，于是由条件有X=0，产生矛盾，故A无非零左零因子.

3）（⇒）当AX=AY时，有A(X-Y)=0，因为A无非零右零因子，所以有X-Y=0，故X=Y.

（⇐）若A有非零右零因子X，则有AX=0=A0，于是由条件有X=0，产生矛盾，故A无非零右零因子.

推论2-8设A∈Pn×n，则∀X，Y∈Pn×n，由XA=YA可推出X=Y⇔由AX=AY可推出X=Y.

〔1〕北京大学数学系几何与代数教研室前代数小组.高等代数（第三版）[M]．北京：高等教育出版社，2003．

O156

A

1673-260X（2013）09-0003-02