数词分类研究述论＊

2013-06-28刘苹

重庆邮电大学学报（社会科学版） 2013年2期

刘苹

（中南民族大学外语学院，湖北武汉430074）

对数词的不同分类方式以及不同类别的称呼方式，体现了研究者对数词系统中不同类别之间关系所持的不同观点以及对与数相关概念的不同定义。现有研究对数词的分类表面上看来差异不大，但是实际上国内每个研究对数词的分类都服务于当时的研究目的，所以分类标准各不相同，分类方式存在着各种各样的差异。分析总结这些分类方式能够了解学界相关的研究状况，分析分类中有分歧的地方有利于廓清相关概念、纠正一些错误的观点以及合理运用相应分类标准，对数词的研究具有重要意义。

一、数词分类研究概况

迄今为止，专门研究数词分类的成果较少，散见于各种语法书或语言教材之中，但是其中也有很多有价值的探索，取得了比较完备的研究成果。相关研究可以总结如下。

从对数词的整体分类来看，有两分法、三分法以及多分法三种。两分法把数词两分为定数（词）和不定数（词）、基数（词）和序数（词），或者简单数词和复合数词。前两种两分法是从功能角度分类，例如，杨树达［1］、黎锦熙［2］、丁声树［3］、张志公［4］、邢福义［5］、萧国政、李英哲［6］、郭攀［7］、刘月华［8］、蒋仁萍［9］等的研究，以及 Routledge Dictionary of Language and Linguistics［10］、Ferdinand von Mengden［11］和王敏、黄锦荣［12］对其他语言数词的分类等；后一种两分法是从结构角度分类，例如朱德熙［13－14］的研究。三分法把数词三分为数目基数（词）、序数（词）和概数（词）或者基数、序数和问数，前者如马建忠［15］和赵世开［16］的研究，后者如王力［17］的研究。王力认为第三类是“问数法”，而马建忠和赵世开认为是“约数（概数）”。多分法把数词多分为基数（词）、序数（词）、分数、倍数、约数、问数、序数，例如廖振佑［18］、胡附［19］、李宇明［20］、张斌［21］、梅轶洁［22］等的研究。这些分类多数只是对数词大体类型的列举，并未从逻辑角度对它们加以整理，只有李宇明和梅轶洁的分类是分了层次的。

从分类角度来看，目前对数词分类有功能属性和形式结构两种角度，大部分是从功能属性角度进行分类，最早从结构角度分类的是朱德熙［13］，之后有李宇明［20］，还有一部分同时采用了两种分类角度，例如赵世开［16］和邢福义［5］。

二、主要分类方式及评价

在这些研究中有下列重要研究成果，这些成果对于数词分类方式既有重要意义又有值得商榷的地方。

朱德熙的《数词和数词结构》是最早系统地研究汉语数词和数词结构的成果之一，该书第一次从结构角度来分析数词和数词结构。其对数词的分类如表1所示，后在《语法讲义》中他做出了一些调整，如表2所示。

表1 朱德熙的数词分类

表2 朱德熙调整后的数词分类

朱德熙的这两个研究区分了数词和数词结构，首次提出了系数结构、系位结构、系位结构组合、复杂的系位结构等概念，对数词的结构分类具有开创性意义。他“从形式和意义相结合的角度描述汉语复合数词的结构，第一次建立了汉语数词的结构系统，其在理论和方法上的贡献都是不言而喻的”，但是仍然存在着下列问题。

第一，系数词和位数词是语法角度的分类，而概数词是概念功能角度的分类，这三者分类标准不一样，不应该放在同一级别。

第二，有些概数表达法不是词而是短语，他所列举的“多、来、好几”本身并不是概数词，而是构成概数表达法的元素或称辅助词，“好些”、“若干”是表达概数的方式却被单列出来，这种分法是不合理的。

第三，他认为“数词有基数和序数的区别。基数表示数量的多少，序数表示次序先后”［14］。这种观点值得商榷：首先，基数和序数的上位概念应该是数。数词是语言术语，确切地说是语法术语，而基数和序数是数学术语；其次，即使把两者相应地改为“基数词”和“序数词”，仍然需要考虑“第三”之类的表达方式到底是数词还是运用数词的有序性表次序，亦即根据“数词是表达数目的语言形式”这个定义，既然序数词特指某一个事物而不是数目，因此“序数词”不是数词。

李宇明阐述了汉语数词的构成要素：数码（语素）：一、二、三……九、十；数位（语素）：十、百、千、万、亿（万万）；数符（语素）：零、分、之、又、点、第，并且以这些构成要素为结构单元考察了数词系统中各个级别的词或短语的构成方式。他认为汉语数词系统由整数、分数、小数、概数和和代数词构成。整数词又有单纯的数码或数位、简单的系位构造、系位组合和复杂的系位构造等几类，代数词有疑问代词和非疑问代词两类［20］。他所构建的系统以数码、数位、数符等语法单元为基础，其论证翔实，结构清晰。但是，因为概数与整数、分数、小数不应该在同一个层面上，同时由于他的研究对象是数学语言并且他认为序数词也是数词，所以他把字母也看作了代数词。

邢福义在《汉语语法三百问》中，对数词分类有详尽的描述［5］，如表3所示。

表3 邢福义的数词分类

他认为基数的表达形式是数词，个位数、段位数、段位系连法构成的复合表数形式（即数词短语）一起构成了基数词系统，倍数和分数都是数量词而不是数词，概数有的是数词有的不是单纯的数词。

在这个分类系统中，“统数”取代了“基数”，与“序数”相并列，这颠覆了数学中基数与序数在数王国中的两分结构，而是把基数与倍数、分数和概数并列于统数之下。这种做法体现了基数、倍数、分数和概数与序数的对立。确实，前几类表达的是数目而序数表达的是次序，它们在功能上是不一致的，而且他把用基数形式表达序数这个现象纳入了系统之中，这在同类研究中是没有的。但是，仔细研究这个系统就可以发现：第一，有一部分混淆了语言意义上的数词与数学意义上的数；第二，该书中提出“位数系连中，有时出现多个段位，这时会形成‘数词结’，严格地说，已经成为‘数词短语’”，但是仍然认为“数词短语”属于“数词”；第三，“统数”是一个新的提法，它在该系统中是“基数”的上位概念，这个“基数”指“由基本数目字表示的确定数目，其表达形式是数词”，但是传统的基数概念是什么，与该系统中基数的内涵是否有冲突，有没有更好的术语来替代，这些都是需要进一步考虑的；第四，这个分类系统与邢福义的《现代汉语》有冲突：《现代汉语》中，基数词包括了表不确定数的词［23］，而《汉语语法三百问》中，表不确定数的词是概数词。

萧国政、李英哲以现有汉语数词的历时研究和共时研究为基础，探讨了基本数词和确数复合词的分类、使用特点和历史演进情况［6］。他们认为数词分为表数数词（基数词）和表序数词（序数词），而表数数词分为述数词和问数词，述数词分类情况如表4所示。

表4 萧国政、李英哲的述数词分类层次

他们的研究陈述了对数词的认识，并第一次提出了“述数词”这个术语以及“整零构造”的概念。整零构造从数值和结构角度解释了一类复合数词，对数词的研究具有重要意义，赵世开曾说过：“关于基数词的结构系统，朱德熙曾经提出过系数词和位数词及系位结构的概念，萧国政与李英哲又增加了‘整零构造’的概念。这就建立了完整的汉语基数词的结构体系。……基数复合数词是系位结构和整零结构两种表数模式组成的体系。”［16］不过，有的学者认为“系位构造/‘十’＋个位数”中的个位数是系数乘以省略了的位数“一”的简写形式，那么，整零构造和系位构造的本质区别是什么、两者是否属于同一层面就需要进一步讨论。同时，该系统中认为基本数词和复合数词的上位概念是确数，确数和概数的上位概念是述数词的观点比其它对数词的描述更合理，不过“确数”和“概数”应表达为“确数词”和“概数词”，而且概数表达很多时候是短语，需要考虑表述方式的一致性。

赵世开把分数、小数和倍数看作固定词组或固定短语，不放在基数词、序数词和概数词一个层面上［16］。他的分类系统如表5所示。

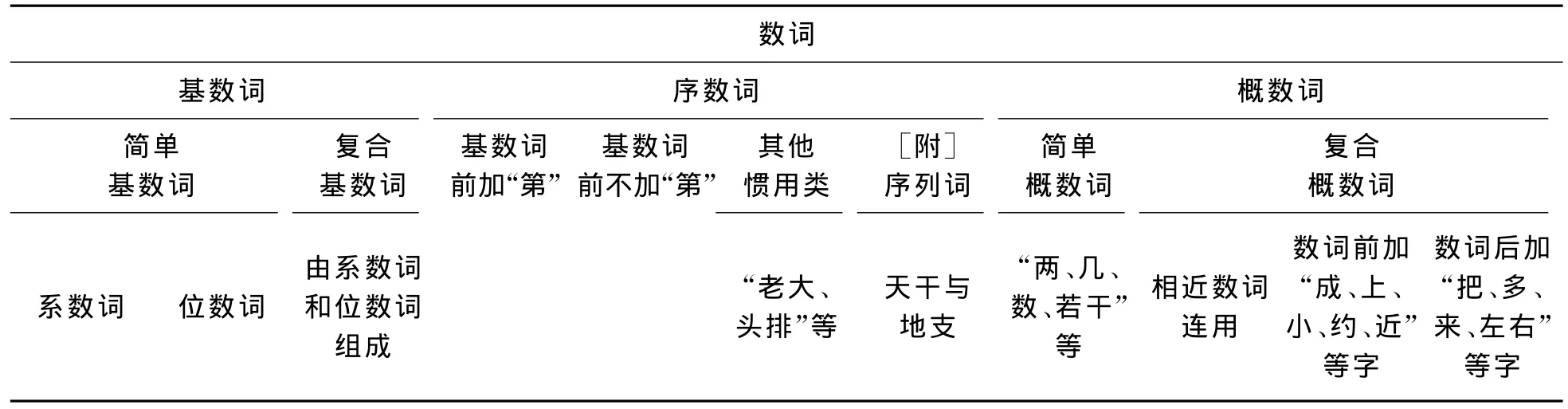
表5 赵世开的数词分类系统

这个研究的优点在对序数词和概数词做了详细分类，但是基数词、序数词和概数词不应放在同一层级，而且，其错误与前文对朱德熙的研究所做的分析一样，序数词及其子类“其他惯用类”和“序列词”严格说来都不是数词。

张斌对汉语数词的讨论较详细，他区分了数词和数，数词是有限的、封闭的，数目是无限的、开放的，把数词分为系数词、位数词、系位数词、数量数词和概数词，并提出表示数目的方法除了直接用数词表示以外，也可以用各种数目表示法来表示，有概数方式，序数方式，倍数方式和分数方式［21］。这个分类方法区分了数词和数以及直接用数词表数目和用数目表示法表数目，这是其特别之处。但是，与前面对其他研究的分析所犯错误一样，序数方式不表数目而是表顺序。

郭攀的《汉语涉数问题研究》是国内专门研究涉数问题的少数专著之一，该书认为数词有基数、序数、倍数、约数（包括问数）和虚数等几类，数词之外还有数词性短语，例如分数。同时，他认为汉语数词中还有一些非典型形式。如：方言数词（廿、卅），俗语数词（幺、方），数量兼容（俩、仨）。他还认为数位分固定性数位和相对性数位，固定性数位又分自然数系和社会性数系（如方位范畴的“一”至“四”，“一”至“八”）。另外，对解释特定数目形式时他使用了几个概念。（1）极数：从程度关系角度表现极致的多；（2）全数：从范围角度定义（如：全部、所有、一切）；（3）成数：从整散关系角度表示不带零头的整数或“多”［7］。

该书材料多样化，论证深入，角度涵盖了语法、语汇和语用，理论视角包括认知心理学和发生学等。“社会性数系”的提出也独树一帜。只是该书主要是以古代汉语数词为研究对象，所选语料多为古代汉语，而且所做研究不够系统，对数词的认识有如下一些问题：第一，基数、序数、倍数、约数等不属于同一级别；第二，他把虚数放入数词之中，不过虚数应该是不同表数方式在语用层面的应用，不属于系统本身；第三，混淆语言意义上的数词与数学意义上的数；第四，“社会性数系”实为对数词有序性的运用而不是数词系统本身的一部分。

国外语言学界（主要是英语语言学界）一般“把数词分为确数词（definite numeral）和模糊数词（indefinite numeral）（见表6），如：ten（十）和several（几）。确数词又可以分为：a.基数词（cardinals）：one（一），two（二），three（三）；b.序数词（ordinals）：first（第一），second（第二），third（第三）；c.分配数词（distributives）：six each（每人六个）；d.频次数词（iteratives）：once（一次），twice（两次），thrice（三次）；e.倍数词（multiples）：eightfold（八重的、八倍的）；f.集合数词（collective numerals）：a dozen（一打）；g.分数词（fractions）：a tenth（十分之一）”［10］。

表6 国外语言学界的数词分类

还有一些只是粗略地把数词分为简单数词和复合数词，并认为不同语言的数词系统都有数基、算子和算术运算符等。例如，Ferdinand von Mengden［11］。

国内对英语数词分类情况也有一些研究，例如赵世开［16］、王敏、黄锦荣［12］等。前者把英语数词分成基数词和序数词，他指出英汉语的数词在分类上大同小异，但在具体表示方法上有较大差异。英语表达数量除用数词之外，还可用可数名词的单复数形式，这和汉语是不一样的。后者通过分析英语数词本身的特点，以伦敦大学编著的《当代英语语法》为主要依据，同时以汉语数词、量词分类为基础，并借鉴俄语、德语的数词分类方法，把英语数词划分为基本数词与合成数词两大类。英语语言学界的分类比一般汉语数词的类别多了分配数词，如：six dollars each（每个六美元），频次数词，如：twice（两次）和集合数词，如：a dozen（一打），这说明英语数词的外延比汉语数词宽泛，在一定程度上反映了英汉数词的差异。两个基本大类的再次分类如表7所示。

表7 王敏、黄锦荣对数词两个基本大类的再次分类

三、数词分类中存在的分歧及原因

总结以上分析，目前数词分类研究总体来说对下列问题的看法有分歧。

1.基数与基数词、序数与序数词概念混淆。尽管多数从功能角度分类的研究都一致认为数词可以分为基数词和序数词，但有的写成基数和序数，有的写成基数词和序数词。对序数词的性质看法也有差异，分别有序数、序数词、序数表达法和序数形式等四种称呼方式，这反映出语言范畴中的“数词”和科学范畴中的“数”两个概念混淆不清。

2.对复合数词到底是词还是短语意见不一致：有些认为“二十二、二百二十二”这类都是数词，有些明确地称之为复合数词，有些则认为它们是词组，如胡附［19］。

3.对基数、序数和确数、概数之间到底应该是上下位关系还是同一级别概念的看法不一。

4.关于倍数、分数、小数表达法的看法不一。以上研究一般都认为数词有基数词和序数词之分，但有些没有涉及倍数、分数、小数的表达法；有些涉及了，但有的把它们放在同一个层级，有的把它们放在不同层级，分属不同的上位概念。

5.对问数词的地位和属性看法不同。有些把问数词放在概数词的下位（如，郭攀［7］），有些把问数词与基数词、序数词并列（如，王力［17］），有的认为问数词不是数词而是疑问代词（如，周彩莲［24］）。

6.对“序数词”、“天然数词”或“社会性数系”到底属不属于数词意见不一致。

7.关于“来”、“多”、“好几”、“若干”、“好些”的看法各不相同，有些认为这些是概数词（如朱德熙［13－14］）；有些认为是助词（如，周彩莲［24］）。

8.有些认为“零”是基数词，外语学界则认为“零”不属于数词，如 Greenberg［25］。

经过分析，数词分类之所以存在以上分歧，主要是因为以下原因。

1.目前学界的研究一般只是从一种语言来定义数词以及考察数词的分类而未参考其他语言的数词，因此难免片面。

2.对数意识、数概念、称数法、数词、科学领域的“数”，以及语法中的“数范畴”等概念混淆不清。

3.分类标准不统一。由于目的不同，不仅采用不同的分类标准，而且在不同级别既有不同标准，也有在同一级别中的杂糅，如梅轶洁［22］把基本数词、合成数词和天然数词及数词辅助词放在同一级别，前面两类是采用的结构标准而后面两类采用功能角度标准来分类，不同的分类放在同一级别中，是不合理的。有的甚至根本就不分，把所有类别全放在一个层面上，例如廖振佑［18］。

4.对数词的定义不准确。目前一致公认的定义是“表示数目和次序的词”，导致了对数词的外延理解过宽。实际上，表示数目和次序的词并非都是数词，而且用来表示数目和次序的语言手段也并非只有词。

5.由于只把视角局限在“词”的范围之内，所以出现了上位概念“词”包括了不是词的下位概念的观象。

6.汉语数词分类受英语语言学的影响。由于英语语言学中认为数词包括基数词和序数词，大多数研究就认为汉语也是这样，而没有考虑到序数词到底是否属于数词，也没有考虑到英语中的“序数词”确实是“词”，而在汉语中却并非如此。

四、分歧解决方案

针对目前数词分类研究中存在的分歧和错误，有必要考察多种语言的数词，对数词进行科学的定义，分清楚科学概念的“数”、语法概念的“数范畴”、“数词”和语义范畴的“数”，在同一级别中采用同一分类标准。

例如，一个以跨语言比较为目的的数词分类系统既需要参照对数词的准确定义，又需要排除因语言差异而带来的结构和语法属性差异等因素，因此可以建立以下分类系统（见表8）。

表8 以跨语言比较为目的的数词分类系统

这个分类系统以“称数法”取代“数词”从而避免了语法属性的不一致，去除序数表达法和基数表达法从而避免把表示顺序的表达方式与表达数目的“称数法”混淆，去除系位结构和整零结构从而避免各种语言数词结构的不同而带来的问题，不包括小数和负数等科学数范畴的概念，也不包括“廿”、“念”、“卅”等方言数词，“幺”、“拐”等俗语数词，“一张、一棵、一吨、一方”等隐语数词以及“俩”和“仨”等数量兼容的数词以及集合数词和频次数词等这些汉语或英语中特有的数词运用层面的现象。因此，这样的分类系统更能经得起推敲，能为跨语言的称数法比较提供更标准的比较框架。

五、结语

本文整理、分析和评价了目前汉英语言学界对数词分类的相关研究，总结了数词分类研究中存在的分歧及原因，证明了只有在准确定义数词的前提下运用合理的标准才能正确地对数词进行分类，才能准确表述各类数词，并在以上分析的基础上尝试提出了一种解决分歧的方案。希望能够通过对学界相关研究状况的梳理，分析分类中有分歧的地方，从而廓清相关概念、纠正一些错误的观点，合理运用相应分类标准，以便更好地进行数词研究。

［1］杨树达.杨树达文集：13［M］.上海：上海古籍出版社，1991：145－152.

［2］黎锦熙.新著国语文法［M］.北京：商务印书馆，1998：89－97.

［3］丁声树.现代汉语语法讲话［M］.北京：商务印书馆，1968：168－179.

［4］张志公.汉语语法［M］//张志公文集：1.广州：广东教育出版社，1991：120－130.

［5］邢福义.汉语语法三百问［M］.北京：商务印书馆，2002：96－99.

［6］萧国政，李英哲.汉语确数词的系统构成、使用特点和历史演进［J］.武汉教育学院学报：哲学社会科学版，1997，16（1）：34－44.

［7］郭攀.汉语涉数问题研究［M］.北京：中华书局，2004：67－98.

［8］刘月华.实用现代汉语语法［M］.北京：商务印书馆：2004：11－150.

［9］蒋仁萍.基数词和序数词的类型学研究［D］.南昌：南昌大学，2007：10－11.

［10］HADUMOD B.语言与语言学词典［M］.北京：外语教学与研究出版社，2000：333.

［11］FERINAND V M.Cardinal Numerals：Old English from a Cross－Linguistic Perspective［M］.Berlin：Walter de Gruyter GmbH ＆ Co.KG，2010：49.

［12］王敏，黄锦荣.现代英语数词单独分类初探［J］.台州师专学报：社会科学版，1998，20（1）：84－87.