初中几何证明应指导学生练好三项基本功

张建刚

摘 要： 几何证明是初中数学学习内容中重要的组成部分。通过几何证明的学习可以培养学生的判断和推理能力，发展学生的逻辑思维能力和严谨的科学态度。作者认为在初中几何证明教学中除了要让学生熟练掌握一些基本证明方法外，还应该指导学生练好三项基本功：一是加强对概念和定理的理解，二是发展几何观念和培养几何直观，三是开阔视野、积累经验。通过这三项基本功的训练为学生做几何证明夯实基础，让学生学习几何证明不再困难，不断体验成功，激发学习兴趣。

关键词： 初中数学教学 几何证明 三项基本功

几何证明是初中数学学习内容中重要的组成部分。通过几何证明的学习可以培养学生的判断和推理能力，发展学生的逻辑思维能力和严谨的科学态度。然而在学生的学习过程中存在如下问题：题与图之间难以对应起来、不会用符号语言描述因果关系和证明过程、证明时候思维混乱无从下手、不会作辅助线等。针对这些问题，我认为在初中几何证明教学中除了要让学生熟练掌握一些基本证明方法，还应该指导学生练好以下三项基本功。

一、深刻理解相关概念和定理

教学中我们不仅要让学生经历概念、定理的形成过程，更要在促进学生深入理解这些概念和定理上下工夫。在几何证明中这些概念、基本事实和相关定理是学生进行几何证明时的出发点和依据，只有对其有深刻理解，才能有效提高学生几何证明的能力。我在平时教学中要求学生对概念、定理的掌握要做到“会说、会画、会写”。

会说就是要能够用语言准确地描述定理的内容；会画就是要能够画出其基本图形；会写就是能够结合基本图形用数学符号语言对定理进行描述。

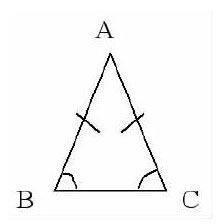
例如：等腰三角形的两个底角相等（等边对等角）。应该能够画出如下图形并用数学符号语言描述。

基本图形：

符号语言：如图，在△ABC中，若AB=AC，则∠B=∠C。

这样可以在深刻理解定理的基础上提高学生识图与画图的能力，培养学生对符号语言的理解和运用能力，为学生进行几何证明打下坚实的基础。使学生在几何证明时，做到既能识别表示各个概念的简单图形，又能在复杂的图形中识别出表示某个概念的那部分图形，并能够熟练运用符号语言进行说理论证。

二、发展空间观念与培养几何直观

《新课标》指出：空间观念主要是指根据物体特征，抽象出的几何图形，根据几何图形想象出所描写实物，想象出实物的方位和它们的相互位置关系，描述图形的运动和变化，根据语言的描述，画出图形，等等。几何直观主要是指利用图形描述和分析问题，借助几何直观，可以把复杂的数学问题，变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习中发挥重要的作用。

显然发展空间观念与培养几何直观对学生学好数学，特别是学好几何证明起到至关重要的作用。关于空间观念是实物和图形之间的关系，一方面是通过实物，根据实物来抽象出几何图形。另一方面是根据几何图形想象出所描述的实际物体，其中一个是抽象，一个是想象。

希尔伯特在他写的《直观几何》序言里头写了这样三层维度。第一层意思，图形可以帮助刻画和描述问题。一旦用图形把一个问题描述清楚，就有可能使这个问题变得直观、简单。第二个层意思，图形可以帮助发现、寻找解决问题的思路。第三层意思，图形可以帮助表述结果，可以帮助记忆结果。

为了帮助学生建立几何直观，在教学过程中我着重训练学生联想和猜想的能力。联想是指在证明过程中看到题目中的相关条件、问题或图形，要能够及时从记忆里提取出相关定理及蕴含其中的因果关系。比如，题目中提到角平分线就要能够立刻想起角平分线的定义和角平分线的两个定理；看到图中有角平分线上的点就想到作这一点到角两边的垂线段；如果求证两个角度数相等，就要想到“同角（或等角）的余角（或补角）相等”“对顶角相等”“全等三角形的对应角相等”等定理；看到图中有直角三角形就要想到“直角三角形的两个锐角互余”“直角三角形斜边上的中线等于斜边的一半”，等等。

猜想不是胡思乱想和任意拼搏，它也是一种科学思维活动。就是依据题目提供的条件与图形结合自己的经验按逻辑推理的规律而进行的思维活动。猜想的结果可能是错误的，这就需要我们去验证、去伪存真。虽然错误的猜想会让我们在证明过程中误入歧途，但是它会给我们的证明提供更多的思路，积累更多的经验。

在教学过程中，我的具体做法如下：一是加强示范，在讲解例题时，把自己的想法和分析问题的思路给学生厘清；二是加强针对性训练，经常找一些针对性强的题目让学生去思考、交流、探讨，帮助他们体验成功，激发兴趣。

我们要加强在此方面的引导和训练，让学生学会正确地联想和合理地猜想。通过训练让学生把数与形、题与图有机结合起来，发展学生的空间观念和几何直观，为学生学好几何证明打下坚实的基础。

三、开阔视野，积累经验

学生在几何证明中感到困难的原因很多，主要是由于缺乏经验，证题经验不足、模式不多，因此对于新的题目常感到不知所措。对于经验的积累，我认为主要包括证明思路和证明技巧两个方面。

几何证明最难莫过于没有思路。怎样积累证明思路呢？这主要靠听讲，看书时积极思考，不仅弄明白“如何证明”，还要进一步追究“证明题方法是如何想出来的”。只有经常这样独立思考，才会使自己的思路开阔。随着证明题难度的增加，还要教会学生用“两头凑”的方法，即在同一个证明题的分析过程中，分析法与综合法并用，缩短已知与未知之间的距离，在教学安排时，要给学生足够的时间思考，而且重复证明思路，提高学生对解题思路的理解和应用能力。

关于证明技巧，其实就是指如何选用合适的定理，如何作辅助线，如何应对运动变换类型的证明题。其中，辅助线的作法是许多学生在几何证明过程中存在的最大困难。

实践出真知，理论问题从实践中提炼的，方法与巧技也是从经验中获得的。俗话说“熟能生巧”，什么是“熟”？“熟”就是经验。不断积累解题经验，探索解题规律，可以充实和丰富解题的经验。

在平时的学习中，我要求学生不仅要多练习还要做个有心人，把一些典型题目的解题方法和思路记录下来，特别是“一图多用”“一题多变”“一题多解”等类型的题目要认真钻研、体会，熟记于心。这样通过长期积累可以有效地提高学生的证题效率，使其掌握更多的证题技巧并形成自己的经验。这些经验和技巧会存放于我们的头脑里，这样在进行几何证明时就能做到胸有成竹，触类旁通。

为了促进学生经验的积累，我们要做好两方面的工作：一是精选题型，我常常就一类型的题目查找大量的中考试卷和各种资料，然后汇编成练习题让学生练习；二是加强检查与考查，定期检查学生的笔记，并在单元检测中或是月考中考查学生掌握的程度。

总之，我们不能总是抱怨学生的错误，现在他们感到有困难，大多是因为刚刚接触这些内容，还没有具备相关的学习经验或者还没有习惯这种说理的方式。只要我们善于引导，勤于训练，鼓励学生勤于思考，善于总结，学生就一定能学好几何证明。