初中数学有效教学三部曲
2013-04-29陈浩
陈浩
【关键词】初中数学 有效教学 情境 问题 应用
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2013)08B-0080-01
要构建有效的数学课堂教学,还得从学生这一主体出发,从学生的兴趣出发,结合生活来引入知识的学习,充分发挥教师的主导作用,以问题为导向,让学生经历问题的分析和解决过程,在掌握知识的基础上应用知识来解决问题,培养学生的实践能力。这样的数学课堂才会更加有效,有利于促进学生的全面发展。
一、创设生活情境,引入知识探究
对教师而言,初中数学教材中所呈现的知识较为简单,从代数的有理数到方程,从几何的一般图形特点到图形的面积计算等都是基础,而对刚上初中的学生来说,这些知识都具有一定的抽象性。因此,如果教师在教学中依旧以灌输式的方式来传授学生知识,学生的兴趣就会被削减,无法更好地理解其中所涉及的概念、公式等,从而让数学学习效率降低。相反,如果教师能从学生的生活实际出发,以直观的情境来引入新知识,促进学生形成从直观到抽象的过渡,借助问题来启发学生的思考,不仅有助于激发学生的学习兴趣,还能更好地引导学生理解相关的概念、公式、定理等。
如在“正负数”的学习过程中,从学生的零花钱的收入、支出说起;在“一元一次方程”的学习中,以体育运动中的路程问题来导入都能较好地激发学生的学习兴趣。但在导入过程中教师要注重根据教学目标来提出问题,启发学生的思维,从而进入新知的探究过程。又如,在全等三角形的学习过程中,教师先给出一个三角形(通过情境展示生活中的三角形物后转化而来),然后引导学生根据三角形三条边的长度、三个角的大小画出并剪下该三角形,同桌对比后,教师提问:“两个三角形的边和角有什么相同点?”通过这样的问题,让学生初步感受“全等”的概念,从而为新知的学习奠定基础。
二、提出问题引导,合作分析解决
教师通过情境激发学生的学习兴趣后,在教学过程中需要借助问题来引导学生对所要学习的知识从简单到复杂、由浅而深地不断探究,在这个过程中,借助问题,形成师生间、生生间的互动,有利于问题的分析和解决。同时,借助互动和反馈,教师能及时了解学生的学习状态,进而调整教学策略,推动课堂教学的发展。因此,在初中数学课堂教学中,教师要注重从学生实际出发,结合教学目标和教学内容来提出具有层次性的问题,引导学生进行合作探究。
如,在“位似图形”的教学中,我先提出问题“什么叫位似图形、位似中心、位似比?”引导学生自主阅读教材,初步理解概念,在学生观察图形后提出问题:“位似图形的位似中心与这两个图形有什么位置关系?任取一对对应点,度量这两个点到位似中心的距离。它们的比与位似比有什么关系?再换一对对应点试一试。”引导各小组学生拿出准备好的位似图形通过观察、测量试验和计算,讨论、交流而得到“位似图形对应点到位似中心的距离之比等于相似比”的结论,教师再引导总结,补充得出“位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比”的结论。这样的学习过程,学生更多的是在教师的引导下完成,而不是被动接受的过程,因此知识的构建更深入。
三、解决实际问题,培养实践技能
学生通过讨论、交流初步构建了知识后,教师就要借助具体问题来引导学生进行解决,从而提高学生解决问题的能力。
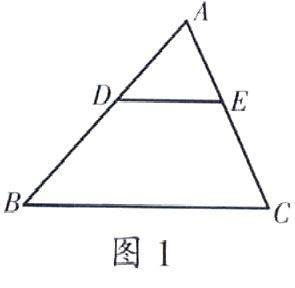
如在“位似图形”的教学中,教师用幻灯片出示问题:如图(1),D、E分别是AB、AC上的点。(1)如果DE∥BC,那么△ADE和△ABC位似图形吗?为什么?(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗?为什么?小组讨论如何解这道题。问题1:证明位似图形的根据是什么?需要哪几个条件?问题2:已知△ADE和△ABC是位似图形,我们根据什么又能得出什么结论?对于问题1教师要指导学生根据位似图形的定义,知道位似图形需要满足两个条件①△ADE和△ABC相似;②对应点所在的直线交于一点。而对于问题2则根据位似图形的性质得出:①对应点和位似中心在同一条直线上;②它们到位似中心的距离之比等于相似比。最后再求证。
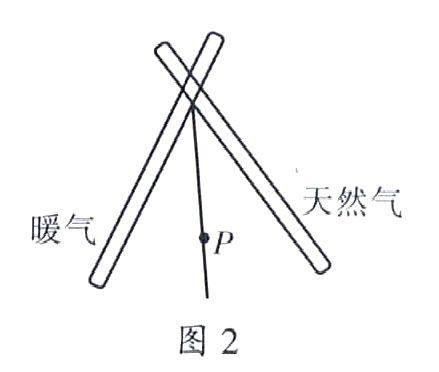
再如,在“全等三角形”的学习后,教师提出问题:小明家居住在一栋居民楼的一楼,刚好位于一条暖气管道和天然气管道所成角的平分线上的P点,要从P点建两条管道,分别与暖气管道和天然气管道相连(如图(2))。问题1:怎样修建管道最短?问题2:新修的两条管道长度有什么关系?画图看一看。通过这样的实际问题来引导学生在分析和解决问题中巩固全等三角形的概念,并能根据所学知识来解决问题,促进学生实践能力的提高。
总之,在新课改背景下,教师在数学课堂教学中要注重突出学生的主体性,通过革新教学观念和教学模式,通过情境导入、问题分析、应用实践来促进学生经历数学学习的过程,促进学生的知识构建和技能培养。
(责编 林 剑)
