省编数学教材“数列”编写意图及教学建议

丁阳

【摘 要】该文从分析比较新旧教材入手，以数列部分为例，剖析新旧教材的基本理念以及新旧教材的结构和难度，以求有助于中职数学老师理解新教材的编写理念，转变传统的教育和教学观念，改变传统的灌输性教学方式，更好地使用新教材。

【关键词】数列 模块 信息化教学 课程难度

新中职教学大纲要求贯彻“以服务为宗旨，以就业为导向”的职业教育办学方针，坚持以学生为主体的教学理念，着眼于学生的全面发展，在培养高素质劳动者和技能型人才上发挥应有的作用。按照教育部2009年颁布的新教学大纲要求编写的新教材，由于与旧教材差别较大，许多教师在不同层面产生了困惑，依然使用旧教材、旧方法组织教学，偏离新教材编写意图。鉴于此，笔者在对“数列”部分进行表层结构、深层结构及难度比较分析的基础上，提出新教材“数列”部分的教学建议。

一、数列部分表层结构的分析

数列部分在基础模块中是第六章，所占篇幅为30页。涉及的知识点包括：数列的定义、等差数列的定义、等差数列通项公式、等差数列前n项和公式、等比数列定义、等比数列通项公式、等比数列前n项和公式。本教材模块设置及特点分析如下：

1.课前导入模块。在章前导入部分，教材通过三个例子意在指出，古今中外，不论是生活还是科学，都能看见数列的影子，数列扮演着重要的角色。本章学习目标和本章目录设置的意图在于使读者明确本章内容的广度与深度，明确学习的内容与目标。

2.思考交流模块。从模块设置中我们可以看出，新教材与旧教材相比，最大的区别就在于采用了“探究——思考交流——问题解决”模式。新教材中的探究性学习模式主要是指情境探索学习，体现的思维比较发散，问题的答案一般不唯一，教材中一般不会为设置的问题提供解答或提示，要靠学生经过自己的思考以及交流讨论获取答案。

3.习题模块。新教材是一个知识点对应安排一个练习，并注意学后练习巩固，每一小节安排一个习题，习题量较少，而且一般是例题的变式或加深题，题量一般不超过10个，全章安排一个复习题，复习题分为A、B两组，A组为基础题，B组为加深题，并且复习题的题量较大。新教材在处理等差中项和等比中项的内容时，没有安排相应的例题，只是把等差中项和等比中项的概念以及习题放在复习题B组中。

4.阅读模块。阅读模块目标：体现数学美，渗透数学文化，了解数学研究新分支——分形几何，感悟大自然中的数学现象。与旧教材相比，新教材阅读模块更有趣味性和科学性。新教材“数列”部分的阅读材料是雪花问题，这首先是一种数学文化的渗透，介绍了数列在数学发展史上的成就，并且可以通过雪花问题锻炼学生的观察能力和空间想象能力，通过这种趣味性的材料引导学生将计算机与数学相结合，培养学生信息化意识，提高学生的应用能力。

5.小结模块。新教材的“回顾与小结”整体篇幅小，其突出特色是配有直观的章节知识框架图，并且以精练的语言高度概括了本章的内容要点和其中蕴涵的数学思想方法。教师利用章节知识框架图可以使学生能够整体把握本章的知识点，并用类比的方法更加透彻地理解本章内容。

二、数列部分深层结构的分析

新教材中，数列一章一共配有8幅插图，新教材中的插图一般都是在探究模块出现，与探究问题的内容相结合，对文字起到了很好的辅助作用，同时也使得学生更加容易理解文字的内容，通过形象生动的图片引起学生注意，激发学生学习的兴趣。“探究——思考交流——问题解决”是新教材的最大亮点，新教材设计了许多不同形式的探究活动，这些都有助于对学生数学思维和数学方法的培养。所谓数学思维，就是指教师在教学活动中，根据数学素材引导学生进行数学形象化的数学构思，形成数学运算。而数学方法是以数学为工具进行科学研究的方法，即用数学语言表述事物的状态、关系和过程，并加以推导、演算和分析，以形成对问题的解释、判断和预测的方法。

新教材在开篇“数列的概念”这一知识点的内容展开中，给出了三个探究问题（见教材P2），抛出这三个问题的意图就是想让学生根据生活实例，使用数学语言表述相关问题，抽象归纳出一般性的数学概念，让学生使用猜想、归纳、抽象等方法，经历整个数学思维过程，使知识内化，形成新的知识结构。

数学思想主要是指数学本身的形成、论证、运算及应用的思想，主要是对数学基础知识和基本方法的本质概括，是在反复理解运用数学概念和方法的基础上形成和发展的。数列虽篇幅不长，但其中蕴含了丰富的数学思想。在解答数列中的有关问题时，充分利用数学思想方法会达到事半功倍的效果。教师应借助例题讲演，让学生领悟并学会应用“数形结合法”与“函数转化法”。

三、新旧教材课程难度比较分析

我们定义影响课程难度（用N表示）三要素：课程的深度、广度和课程时间。其中，课程广度（用G表示）就是指课程中包含的知识点的多少，我们用知识点的数量来表示；课程深度（用S表示）则是指各个知识点的掌握程度，我们用大纲要求的不同程度来表示；课程实施时间（用T表示）是指按照教学计划的课程内容的安排时间，用大纲中的“课时”来表示。这样，我们可以建立课程难度的数学模型如下所示：

N=λ·G/T+（1-λ）·S/T

在这个模型中，其中G/T表示单位时间的课程广度，S/T表示单位时间的课程深度，λ称为加权系数，且满足0<λ<1。

1.难度模型的相关说明。

（1）课程广度。为了量化新旧教材数列部分的广度，我们用数列的知识点的个数来量化。因为新旧教材都是依据大纲编写的，故我们根据大纲中数列部分的内容进行统计。

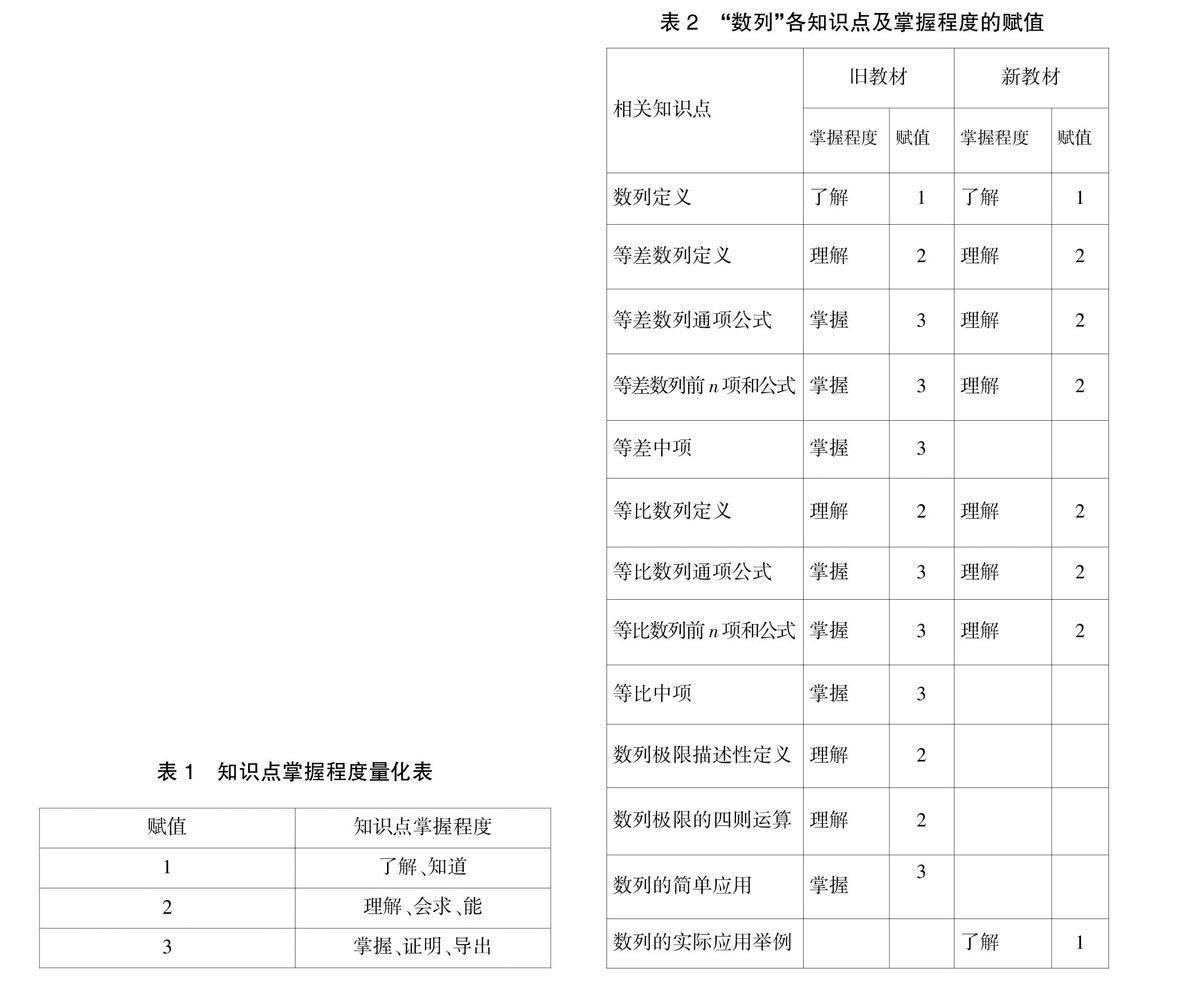
（2）课程深度。由于大纲对各个知识点的要求不同，我们根据大纲要求将不同的认知要求进行赋值，以此量化课程深度，如表1所示。

表1 知识点掌握程度量化表

（3）λ的取值。λ是一个经验常数，根据现有研究成果，专家学者普遍认为课程广度对课程难度的影响较大一些，故取值为λ=0.6。

2.新旧教材数列部分课程难度的量化比较。数列部分课程时间的确定。根据旧教材数列部分内容的课时安排情况确定为14课时，即T1=14；而新教材数列部分内容的课时安排总计10个课时，即T2=10。

根据上文中确认知识点以及赋值法，我们将新旧教材数列部分的知识点及对知识点的掌握程度用表2罗列出来。根据此表数据，可以得出新旧教材课程广度和课程深度（见表3），并可以分别求出两本教材中数列部分的可比广度和可比深度（见表4）。

表2 “数列”各知识点及掌握程度的赋值

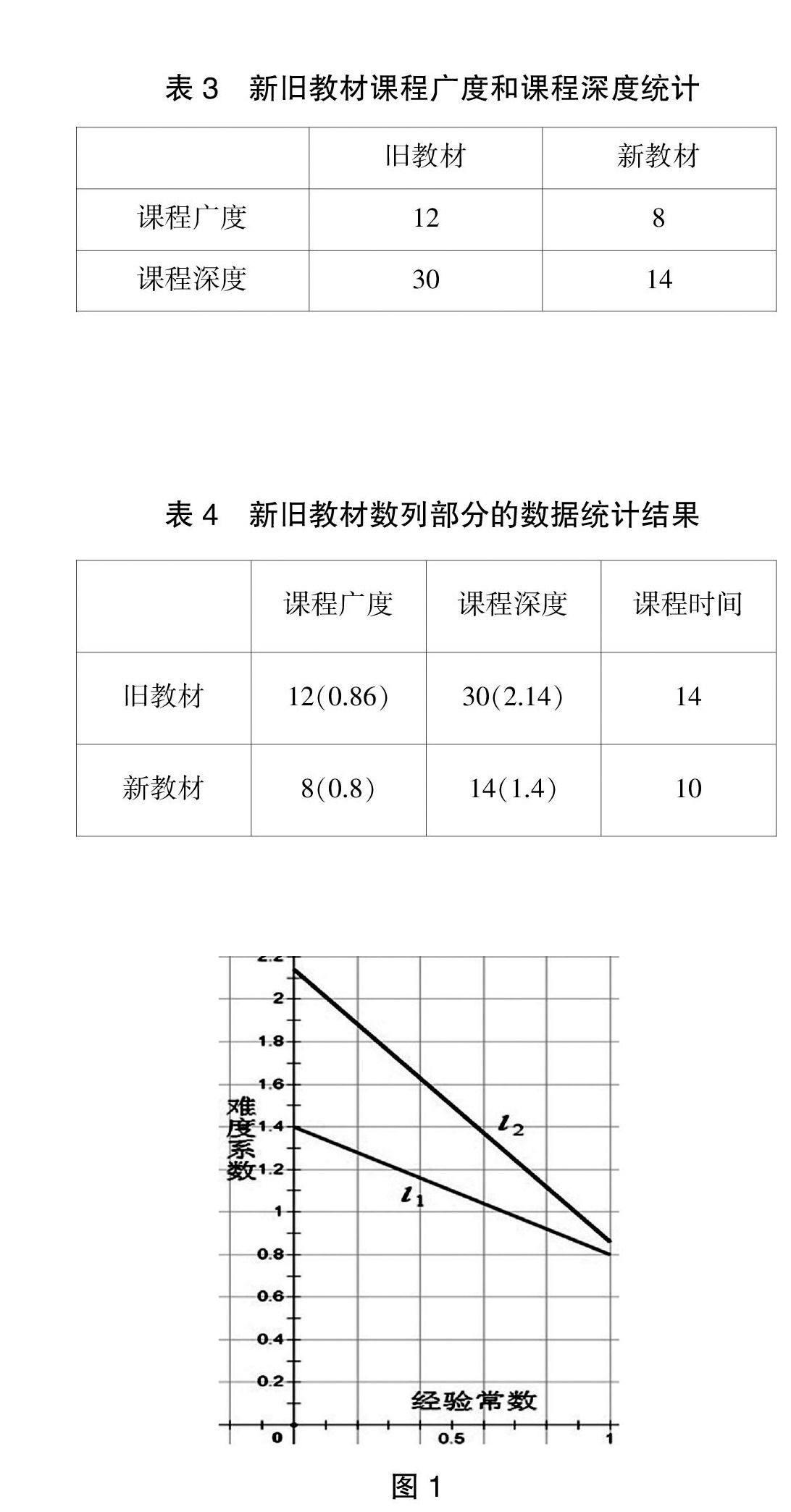
表3 新旧教材课程广度和课程深度统计

旧教材的可比广度为G1/T1=0.86，可比深度为S1/T1=2.14；新教材的可比广度为G2/T2=0.8，可比深度为S2/T2=1.4。

表4 新旧教材数列部分的数据统计结果

所以根据所建立的模型，分别表示出新旧教材数列部分的课程难度：

N1=0.80·λ+1.40·（1-λ）=1.4-0.6·λ

N2=0.86·λ+2.14·（1-λ）=2.14-1.28·λ

由于0<λ<1，故0.8

如果λ=0.6，那么N1=1.04，N2=1.37。

3.新旧教材数列部分课程难度对比结论。

由图1可以看出，直线l1表示新教材数列部分课程难度系数值N1，直线l2表示旧教材数列部分课程难度的N2，由于0<λ<1，无论λ如何取值，线段l1始终在线段l2的下方。

结果表明，与旧教材数列部分的难度相比，新教材的难度有所下降，这主要是因为新教材数列部分的课程广度以及课程深度都比旧教材的要低。

四、新教材使用教学建议

新大纲倡导的数学教学是师生之间、生生之间交流互动与共同发展，让学生都能获得必需的数学知识，使学生得到全面发展。以下几点教学建议仅供教师使用新教材时参考。

1.新教材使用时，教学要突破“定义-定理-证明”的传统教学方式，不必拘泥于严格的演绎推理，可从具体的生产或生活实例进行探究引入课题，导出相关概念，关注学生的直觉感受和已有经验，并把它们提升到数学理论的高度。挖掘“思考交流”的深度，使学生真正内化知识，形成新的认知结构。充分利用“问题解决”强化学生应用数学的意识，强化学生用数学的眼光看世界的能力。

2.按照大纲的要求，数列概念的引入、等差数列、等比数列的学习都要结合学生生活实例和不同专业背景来进行设计。因此，教师在教学的过程中要精选一些典型的、适合学生的生活情境，从实际应用的角度去引出概念，调动学生的学习主观能动性，提高教学效率。

3.本章节的重点是等差数列和等比数列。等差数列和等比数列在知识内容和思想方法上都很相似。在学习了等差数列后，建议教师引导学生用比较学习法，类比于等差数列的通项、性质以及前n项和等，自主探索等比数列的相应问题。

4.关于信息化教学的引入。根据教学大纲要求，培养学生计算工具使用技能。信息化时代智能化计算工具的使用应该成为学生的必备技能。本章节借助计算机辅助教学，可以在学习过程中起到化繁为简的作用，如“正方形筛子”的建立等。

5.本章节的“探究”“问题解决”以及例题和习题中，有许多来源于古代数学和现代数学的素材，如“出门望九堤”“雪花问题”等，还有很多来源于实际生活情境，体现了数学文化价值的题目，如“麦田怪圈”“分形几何学”等。教学中要注意加强与实际生活的联系，同时也要注意利用这些资源，提高学生学习本章节内容的兴趣，调动学生学习的积极性和主动性。

（作者单位：江苏省连云港中等专业学校）