一种混合动量轮系的故障重构策略研究*

随着卫星应用技术的发展，快速机动能力已成为遥感卫星的基本功能需求.快速机动对控制系统执行机构的力矩输出能力和力矩输出精度均提出了很高要求.目前，快速机动可以选用推力器，也可以选用控制力矩陀螺[1]，但从寿命、质量、可靠性以及成熟度等方面综合考量，固定安装的动量轮以其良好的技术基础、成熟的使用方法在完成快速机动任务方面得到了广泛应用[2-5].

本文提出了一种动量轮混合配置策略，选用4个0.5N·m大力矩动量轮和4个0.1N·m小力矩动量轮.执行机构主份采用4个大力矩动量轮，用于完成快速机动及控制任务，备份采用4个更为成熟的小力矩动量轮在故障重构时使用，从而提高整个轮系的可靠性.本文给出了在故障重构且维持整星零动量情况下，混合轮系中各动量轮标称角动量的分配方法，重构后单轴能够输出的最大力矩以及分配矩阵算法.

1 一种混合动量轮系故障重构方法

1.1 一种混合动量轮系配置

考虑卫星控制系统的可靠性，采用4个大力矩动量轮和4个小力矩动量轮作为控制系统执行机构，大力矩动量轮最大可以提供0.5N·m的控制力矩，小力矩动量轮最大可以提供0.1N·m的力矩，两种动量轮可以提供的最大角动量均为25N·m·s.

8个动量轮采用塔形结构，每个动量轮自身标称角动量方向与卫星-y轴夹角均为45°，动量轮在卫星xoz面上均匀分布，其中标号为1，2，3，4的动量轮为大力矩动量轮，标号为5，6，7，8的动量轮为小力矩动量轮，安装示意图如图1所示.动量轮自身标称角动量方向在卫星本体坐标系的分量如式(1)所示.

图1 混合轮系8个动量轮在卫星本体上的安装

(1)

8个动量轮在卫星3个轴上的角动量分量矩阵为H，H矩阵中第1～8列，分别表示标号为1～8的动量轮角动量在卫星3个本体轴上的分量.

卫星正常工作时采用4个大力矩动量轮，整星构成零动量.当大力矩动量轮中的一个或几个故障时，可以采用小力矩动量轮代替.

为了讨论方便，约定符号定义如下:

hwi：表示i号动量轮角动量，i=1，2，…，8；

h：表示整星角动量矢量；

A：表示动量轮系角动量矢量转换为在整星角动量矢量的转换矩阵；

D：表示三轴力矩分配在各动量轮上的力矩分配矩阵；

T1，T2，T3，T4：表示4个轮子的力矩输出分配；

Tx，Ty，Tz：表示轮系能够提供的三轴力矩输出；

TMi：表示i号动量轮能够提供的最大力矩输出.

1.2 混合轮系故障重构的原则

对于混合轮系故障重构，主要考虑两个原则：

一是轮系重构后要计算整星零动量下各轮标称角动量，标称角动量的选取应避免轮子转速偏离原标称转速过大，使动量轮控制容量受到限制，也避免转速在0附近[6-7]，影响使用寿命；

二是计算动量轮力矩分配矩阵时，要考虑某个动量轮饱和时，在控制轴方向能提供最大力矩.

1.3 混合轮系故障重构的方法

1.3.1 混合轮系配置计算

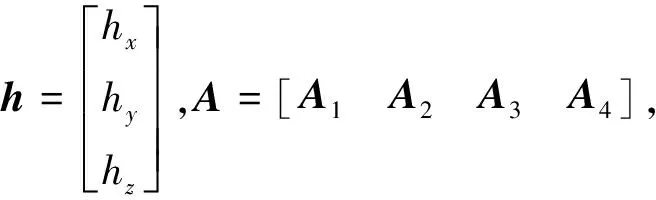
矩阵D表示力矩分配矩阵，D阵采用伪逆计算：

D=AT(AAT)-1

(2)

则hw=Dh.

显然，对于1～4号轮子的安装构型，在整星零动量时，其标称角动量大小一样，可以1、3号动量轮正转，2、4号动量轮反转.

1.3.2 混合轮系故障重构方法

如果1～4号动量轮中有轮子故障，可以选用5～8号相应动量轮替换.例如：

1号故障，可以选择5～8号中的任何一个替代；

1、2号故障，可以选用5～8号中的任何两个替代；

1、3号故障，也可以选用5～8号中的任何两个替代；

可见，故障重构的方式有很多种，可以根据重构方法，计算出替代方案下各动量轮的标称角动量，以及所能提供的各轴最大力矩，从中选取最优方案，完成轮系故障重构.

1.3.2.1 混合轮系标称角动量计算

在故障重构时，不管怎么替换，只考虑4个动量轮工作的情况.对于被替换的动量轮，把A阵中的相应列替换为动量轮在H阵中的相应列，得到故障重构后新的A阵.

要实现整星零动量，需满足h=Ahw=0.

(2)

由此可得4个工作的动量轮之间的比例关系，确定一个动量轮的标称转速后，要保持整星零动量，就得到了其他3个动量轮的标称转速.

1.3.2.2 混合轮系提供的最大控制力矩计算

本文研究的混合轮系如1.1节所述，由于1～4号动量轮最大可以提供0.5N·m力矩，5～8号动量轮最大可以提供0.1N·m力矩，如果主份1～4号动量轮有故障情况发生，需要用5～8号动量轮顶替，这时，继续采用伪逆计算方法计算力矩分配矩阵D，可能在某轴输出力矩很小时就有轮子饱和.

由于是4个轮子输出力矩，合成三个轴的力矩输出，因此存在一个方向自由度，也就是说可以有多种力矩分配阵，只要满足AD为单位阵即可.下面给出了一种力矩分配矩阵计算方法，利用这种方法，可以求出针对上述混合动量轮系输出最大力矩的分配矩阵，也可以推广到其他构型的混合轮系使用.

由于AD为单位阵，因此：

分析第一个公式(其他两个式子后续分析方法相同)：

可得：

记为：

(3)

可以看出，d11可以任意选取.

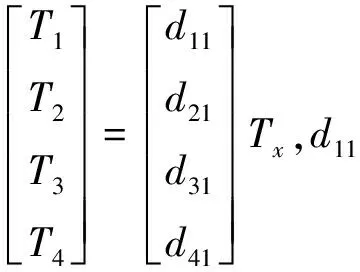
根据上述原理，d11作为变量时确定出x轴输出的最大力矩：

Tx=min(max(Tx1,Tx2),

max(Tx1,Tx3),max(Tx1,Tx4))

同时确定出d11，根据式(3)可以确定出d21、d31、d41.

具体求解最大力矩过程中，还需要考虑xi1、xi2是否为0等具体情况，但原理均为上述方法，可以具体问题具体分析.

其他两个轴可以同样考虑，利用类似的方法得到D阵的另外两列.

2 混合轮系重构计算结果分析

根据上述方法，编制程序，按照混合轮系故障重构的最优原则，迅速计算出力矩分配阵D，同时确定出每轴可以提供的最大力矩.

2.1 计算结果

根据上述方法，计算了1号动量轮故障，分别用5～8号动量轮替换的结果；计算了1、2号动量轮故障，用5～8号中任意两个动量轮替换的结果；同时计算了1、3号轮子故障后，用5～8号中任意两个动量轮替换的结果，具体计算结果见表1至表3.可以根据计算结果，选择最优的重构方案.

表1 动量轮1故障后轮系重构计算结果

表2 动量轮1、2故障后轮系重构计算结果

续表

表3 动量轮1、3故障后轮系重构计算结果

如果选用直接伪逆计算，例如对于1号动量轮故障，选用5号代替，得到的力矩分配矩阵为

由于5号动量轮的饱和力矩是0.1N·m，因此三轴可提供的最大力矩为：

显然，直接用伪逆计算得到的分配矩阵，其提供的三轴力矩，远小于本文计算方法所得结果.后续多轮故障重构也有类似结论.

2.2 可选的重构方法

根据计算结果，可以得到如下重构策略：

对于轮子1故障，可以优先选用相邻的轮5或轮8代替.若用轮6或轮7替换轮1，会造成其中的一个轮子标称角动量较低.

对于轮子1、2故障，从力矩输出和标称角动量方面考虑，可以优先选用轮子5、6或5、8或6、8来替换.

对于轮子1、3故障，从力矩输出和标称角动量方面考虑，可以优先选用轮子5、7或5、8或6、7或6、8来替换.

对于其他类似的单个轮子或两个轮子故障，可以通过相同方法，得到轮系重构的替换方案.

3 结 论

本文给出了一种混合轮系基于单轴输出最大力矩的故障重构力矩分配矩阵计算方法，给出了重构后保持整星零动量时各轮标称角动量计算方法，同时进行了一个轮子或两个轮子故障后的各种重构计算，给出了优选的重构方法，这些计算方法可以推广到其他构型的混合轮系使用，在实际工程应用中具有很强的参考意义.

参 考 文 献

[1]刘刚，李传江，马广富，黄静. 应用SGCMG的卫星姿态快速机动控制[J] 航空学报, 2011, 32(10): 1905-1913

Liu G, Li C J, Ma G F, Huang J. Time efficient controller design for satellite attitude maneuvers using SGCMG[J].Acta Aeronautica ET Astronautica Sinica, 2011, 32(10): 1905-1913

[2]陈志明，刘海颖，王惠南，叶伟松. 采用动量轮及推进器的微小卫星的姿态机动控制[J] 中国惯性技术学报, 2009, 19(5): 526-532

Chen Z M, Liu H Y, Wang H N, Ye W S. Attitude maneuver of micro-satellite using thruster plus bias momentum wheel[J]. Journal of Chinese Inertial Technology, 2009, 19(5):526-532

[3]陈新龙,杨涤,翟坤. 某型卫星的零动量反作用轮姿态控制技术研究[C]. 第25届中国控制会议, 哈尔滨, 2006

Chen X L, Yang D, Zhai K. Attitude control technology study based on zero momentum reaction wheels of a certain satellite[C].The 25thChinese Control Conference, Harbin, 2006

[4]张振民,李傲霜,杨涤. 月球探测器姿态大角度机动的反作用轮控制[J] 飞行力学, 2003, 21(2): 53-55

Zhang Z M, Li A S, Yang D. Reaction wheels control for lunar probe attitude large angle slew[J]. Flight Dynamics, 2003, 21(2): 53-55

[5]Creamer G, Delahunt, Gates S P, et al. Attitude determination and control of Clementine during lunar mapping [J]. Journal of Guidance Control and Dynamics, 1996, 19(3):505-511

[6]John B S. Reaction wheel low-speed compensation using a dither signal [J]. Journal of Guidance Control and Dynamics, 1993, 16(4):617-622

[7]Tehrani E S, Khorasani K, Tafazoli S. Dynamic neural network-based estimator for fault diagnosis in reaction wheel actuator of satellite attitude control system[C]. The Internationl Joint Conference on Neural Networks (IJCNN), Montreal, QC, Canada, 31 July- 4 Aug, 2005

[8]章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社,1998:270-278