一种基于B平面参数的深空天体接近段自主轨道控制方法*

深空探测指脱离地球引力场进入太阳系空间和宇宙空间的探测.深空探测器处于星际航行，相比地球卫星和月球探测器，面临飞行距离远、时间长和环境未知性强等问题，传统的依靠地面测控的航天器导航与控制方法在实时性、成本和资源上受到种种限制，很难满足深空探测任务的需要，因此自主导航与控制是完成深空远距离天体捕获和环绕探测任务的关键技术.目前，绝大多数星际轨道制导的目标参数都转换为B平面参数[1].文献[2]提出了一种基于B平面参数的深空探测转移轨道自主中途修正的方法，本文对其进行了进一步研究，将该方法应用于接近目标天体段的自主轨道控制，并通过误差椭圆来统计修正后B平面靶点不确定性，最后以火星探测为例进行了蒙特卡罗仿真，验证了该方法的正确性.

1 B平面参数

Kizner[3]发现建立在目标天体B平面上的参数与探测器飞行轨道状态参数之间存在较好的线性关系.大量理论分析和工程实践表明可以用B平面参数来描述探测器的飞行目标轨道的散布，并且用迭代方法修正B平面参数的误差具有很好的收敛性，因此B平面参数广泛应用于深空探测的轨道设计和优化中.

一般来说，深空探测器到达目标天体附近时的速度超过了相对目标天体的逃逸速度，因此探测器在目标天体附近将以双曲线轨道飞行.B平面定义为通过目标天体中心并垂直于探测器进入轨道的双曲线渐近线方向的平面，渐近线方向为距离目标天体无穷远时的速度方向，可以近似为探测器进入目标天体影响球时的速度方向.

B平面坐标系定义如图1所示，以目标天体中心为原点，记进入轨道的渐近线方向的单位矢量为S，记某参考方向的单位矢量为N，则S与N的矢量积为T轴，R轴由S轴和T轴按右手法则确定.参考方向N理论上可以取任何方向，原则是便于建立目标轨道参数与B平面参数之间的解析关系，如研究火星探测时可取N为火星赤道面法线方向.B矢量定义为由B平面原点指向探测器轨道与B平面交点的矢量，B矢量大小为双曲线的短半轴长度.B平面参数BT和BR定义为B在T轴与R轴的分量.

BT=B·T，BR=B·R

(1)

图1 B平面坐标系示意图

2 自主轨道控制

自主轨道控制指深空探测器在无地面干预情况下利用导航信息自行计算修正轨道所需控制量并予以执行.由于不可避免存在变轨误差、导航误差等因素，导致探测器实际轨道偏离设计轨道，因此需要对探测器进行轨道修正以满足设计要求.

深空探测器轨道的终端状态为初始状态的函数，初始状态P为当前时刻探测器的轨道参数位置和速度，终端状态Q根据目标轨道的要求不同而选择不同参数，一般将目标参数转换为B平面参数，则函数形式为

Q=f(P)

(2)

线性制导方法(又称摄动制导)的基本思想为探测器的实际轨道与标准轨道的偏差为小量，从而将实际轨道在标称轨道附近泰勒展开，取到一次项进行研究.

将实际轨道在标称轨道附近泰勒展开保留线性项，得到如下线性控制方程：

(3)

其中：ΔQ为终端时刻探测器标称状态Qnom与实际状态Q的偏差，即ΔQ=Q-Qnom；ΔP为控制向量；K为状态变量对控制参数的敏感矩阵.

B平面参数的误差定义如下：

ΔBR=BR-BRnom

(4)

ΔBT=BT-BTnom

(5)

则

ΔQ=[ΔBRΔBT]

(6)

修正时刻选定后，探测器位置量不可改变，可变的只有速度量，因此控制量为速度增量Δv，利用最小二乘方法计算得到控制量

Δv=ΔP=(KTK)-1KTΔQ

(7)

用这个控制量来修正初始状态，再重新计算B平面误差、敏感矩阵和速度增量，这样反复迭代直到终端状态满足一定的精度要求.

线性制导方法的关键在于计算敏感矩阵，方法有分析法和数值法两种.分析法通过建立近似模型用解析方法求得偏导数，数值法用数值计算方法将状态参数各自取微小变化去除相应的B平面参数的改变得到偏导数.为了减小由于非线性动力学模型导致的状态转移矩阵计算误差和避免大量的积分运算，本文采用了数值微分方法计算敏感矩阵[4].

(8)

以上面矩阵中第一个元素为例，给出偏导数的计算公式如下：

(9)

其中，ε是小幅值摄动量，即速度增量Δv.

3 误差椭圆

B平面靶点的不确定性可利用误差椭圆给出[5]，如图2所示.误差椭圆作为地面事先评估轨道修正效果的一种手段，可用于变轨点的优化选择.B平面上靶点分布可通过导航系统给出的误差协方差阵近似选取，将当前时刻的估计状态的误差协方差阵时间更新到探测器与B平面相交时刻，利用该协方差阵得到误差椭圆的大小以及方向.

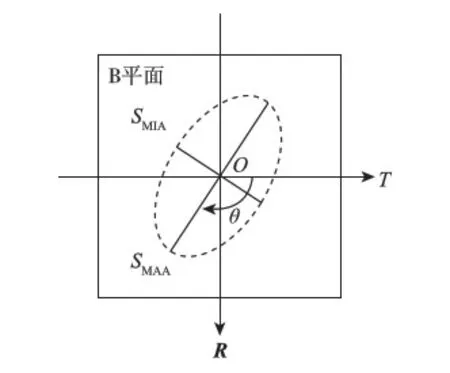
图2 B平面误差椭圆示意图

状态变量取以目标天体为中心的惯性系下探测器的位置和速度矢量，令P0(r,v)为当前时刻探测器位置和速度的误差协方差阵，其中当前时刻的r为修正前的位置矢量，v为引入速度增量Δv并考虑一定的轨控执行误差修正后的速度矢量，Pf(r,v)为终端时刻探测器位置和速度的误差协方差阵，则有

Pf(r,v)=Φ(tf,t0)P0(r,v)ΦT(tf,t0)

(10)

其中Φ(tf,t0)为当前时刻t0探测器位置矢量和速度矢量到终端时刻tf探测器位置矢量和速度矢量的状态转移矩阵，轨道控制误差通过状态转移矩阵影响B平面误差散布.

(11)

令A为PSTR阵中对应探测器T、R轴位置误差协方差阵，可以表示为

(12)

式中σT、σR分别为BT、BR的误差方差，μ为BT和BR的相关系数.

假设B平面参数的统计量服从二维正态分布，则有概率密度函数

(13)

当概率密度fRT为定值时，在B平面坐标系中的图形是椭圆，椭圆的大小和方向由σR、σT和μ定义，有

(14)

相关系数μ的数值一般不必计算，可通过坐标系的旋转变换将其化为0，对于实对称矩阵A有如下变换：

D=XTAX

(15)

其中，D是以A的特征值λ1和λ2为主对角线元素的对角阵，X是由对应特征向量的标准正交基构成的矩阵，则椭圆方程如下：

(16)

其中，(x′,y′)是旋转后的新坐标系.当M分别取1、2和3时，得到椭圆分别称之为1σ、2σ和3σ误差椭圆.

设λ1>λ2，则概率误差椭圆的长半轴、短半轴计算公式如下：

(17)

设特征值λ1对应的特征向量为u1，u1T为特征向量u1在B平面T轴的分量，u1R为特征向量u1在B平面R轴的分量，则误差椭圆的方向角为特征向量u1在B平面内的方位

(18)

对于二维正态分布，Nσ误差椭圆之内的概率由下式给出：

(19)

从表1可以看出，B平面靶点在3σ误差椭圆外的概率很小，因此在打靶时以3σ形式绘制误差椭圆.

表1 二维正态分布的Nσ概率

4 数学仿真

以火星探测为例进行接近目标天体段自主轨道控制仿真，标称轨道为双曲线轨道，近火点历元时刻2014年10月8日12时，轨道根数(半长轴，偏心率，倾角，升交点赤经，近火点幅角，真近点角)分别为(-3712.876km，2.07652，40.0°，177.698°，257.483°，0.0°)，则设计的目标B平面参数分别为BR=3603km，BT=5716km，近火点高度为600km，要求目标天体捕获轨道高度精度优于50km(3σ).

设到达近火点前12小时，火星探测器实际轨道的位置误差和速度误差分别为(500km，500km，500km，20m/s，20m/s，20m/s)，修正前探测器到达近火点的B平面参数误差ΔBR=-1087.551km，ΔBT=2051.362km，近火点高度误差为1246km，不满足指标要求，需要对其进行轨道修正.

探测器以火星方向矢量和火星视半径为观测量进行6小时自主导航，导航敏感器测量误差0.01°，系统误差0.001°，导航初始时刻的位置误差和速度误差分别为(10km，10km，10km，1m/s，1m/s，1m/s)，到达近火点前6小时，以自主导航结果进行B平面参数制导律计算，得到速度增量为vx=-35.28m/s，vy=-76.43m/s，vz=-38.66m/s，实际轨控执行时引入了0.1%的大小随机误差和0.1°的方向随机误差，修正后探测器到达近火点的B平面参数误差ΔBR=2.177km，ΔBT=23.985km，近火点高度误差为7.749km.

由于探测器不可避免存在未知的导航误差、轨控执行误差等因素，因此采用蒙特卡罗法进行仿真分析是一个直观有效的途径，它是通过对实际过程的大样本仿真试验得到对未知随机事件的统计信息.本文进行500次蒙特卡罗仿真，通过误差椭圆来统计B平面靶点的不确定性，由于每次仿真都可以计算得到一组误差椭圆参数(SMAA、SMIA和θ)，取500次仿真结果的平均值来绘制最终的误差椭圆，打靶结果如图3～4所示.从图中可以看出轨道修正后B平面靶点都在3σ误差椭圆范围内，长半轴SMAA为48.89km，短半轴SMIA为27.01km，方向角θ为-143°，统计近火点轨道高度误差为27.094km(3σ)，满足指标要求.

图3 轨道修正后B平面误差

图4 捕获的近天体高度误差

5 结 论

本文研究了深空探测器接近目标天体段的轨道控制问题，提出了以B平面参数为制导目标参数的自主轨道控制方法，并通过误差椭圆来统计修正后B平面靶点不确定性，最后以火星探测器为例进行了蒙特卡罗仿真，仿真结果表明利用该方法进行轨道修正后B平面靶点都在3σ误差椭圆范围内，近火点轨道高度精度优于50km(3σ)，验证了该方法的正确性.

参 考 文 献

[1]杨嘉墀，吕振铎，孙承启，等.航天器轨道动力学与控制[M].北京：宇航出版社，2002

[2]张晓文，王大轶，黄翔宇.深空探测转移轨道自主中途修正方法研究[J].空间控制技术与应用，2009，35(4)：27-33

Zhang X W, Wang D Y, Huang X Y. Study on the autonomous midcourse correction during cruise phase of interplanetary exploration [J]. Aerospace Control and Application, 2009，35(4)：27-33

[3]Kizner W. A method of describing miss distances for lunar and interplanetary trajectories [J]. Planetary and Space Science, 1961, 7：125-131

[4]Desai S D, Bhaskaran S, Bollman W E. The DS-1 autonomous navigation system: autonomous control of low thrust propulsion system[C]. AIAA Guidance, Navigation and Control Conference, New Orleans, USA, August 1997

[5]Tapley B D, Schutz B E, Born G H. Statistical orbit determination [M]. Burlington：Elsevier Academic Press, 2004