挠性多体卫星星间跟踪天线回扫运动研究*

随着航天任务的需求，很多卫星(如中继卫星[1])需安装星间跟踪天线(以下简称天线)完成目标星的指向、捕获和跟踪.星间跟踪天线通常为柔性结构，导致整个航天器的动力性特性非常复杂，呈现大柔性、多体耦合和非线性等特点，给卫星的控制系统设计提出了很大的挑战.

为保证有效的星间通信链路，天线需实现高精度的指向跟踪，但天线的指向跟踪运动与星体的姿态运动存在强烈的耦合，同时天线的指向跟踪运动还会激起天线的柔性振动，这些因素都会影响天线的指向精度，造成星间通信无法正常工作.因此，研究挠性天线的指向跟踪控制就显得非常重要.

挠性多体卫星动力学是进行天线指向跟踪控制研究的前提.国内外很多专家学者都开展了相关的研究，形成了很多研究成果，其中基于分析力学的建模方法由于推导简单而被广泛使用，如拉格朗日方程[2]、凯恩方法[3]等.本文拟采用混合坐标描述方法[4]和拉格朗日方程结合的建模方法完成挠性多体卫星的动力学建模.

挠性天线指向跟踪控制是近年来的研究热点之一[5-7].文献[8]将天线指向跟踪过程分为回扫、捕获和自动跟踪3个过程，由于回扫过程天线运动幅度较大，对星体姿态运动和天线柔性振动的耦合影响也较大.针对天线回扫运动，Bang-Bang控制是一种常用的控制方法，该控制是从时间最优角度考虑的，并不能解决天线回扫运动的耦合影响.Tyler[9]设计了一种类似Bang-Bang控制的轨迹预处理算法，可通过配置生成轨迹的速度和加速度减小耦合影响，但每次设计都需知道回扫的角度和回扫时间，不便于实际应用.而Gawronski等[10]为适应实际执行机构的速度和加速度限制，提出了一种命令预处理算法，该算法可减小天线运动结束时的振动，并且可避免出现超调，已应用于很多天线的指向控制.

本文以安装星间跟踪天线的中继卫星系统的某用户星为对象，研究挠性天线的回扫控制.具体内容包括：首先建立挠性多体卫星的动力学模型，然后采用命令预处理算法设计天线回扫指令，解决天线回扫运动对星体姿态稳定和柔性振动的影响，最后进行仿真验证.

1 挠性多体卫星动力学建模

1.1 系统描述

为研究方便，忽略太阳帆板等附件，卫星中心体只安装支撑杆连接的抛物面天线，具体结构如图1所示.

卫星中心体为刚体，存在姿态运动.有限元分析表明：天线的固有频率比支撑杆的固有频率要高很多.因此可把支撑杆简化为只有振动的柔性附件，把天线简化为只有转动的刚体附件.

为描述系统各体之间的相对运动，定义如下坐标系：

(1)卫星本体坐标系ObXbYbZb(简称b系)

原点Ob是卫星质心，3个坐标轴分别沿着星体的惯量主轴，单位向量为b.

(2)支撑杆本体坐标系Oa1Xa1Ya1Za1

坐标原点Oa1位于支撑杆与卫星平台的连接处，Oa1Za1平行于ObZb，但方向相反，Oa1Xa1平行于ObXb，但方向相反，Oa1Ya1平行于ObYb同向，单位向量为a1.

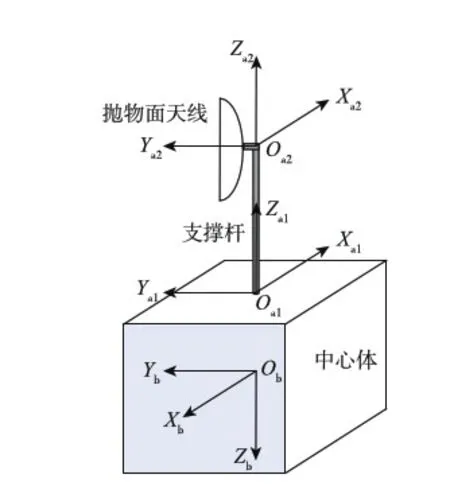
图1 卫星结构示意图

(3)天线本体坐标系Oa2Xa2Ya2Za2

坐标原点Oa2位于天线俯仰轴和方位轴相交处，Oa2Xa2与天线俯仰轴重合，Oa2Ya2与天线视轴重合，Oa2Za2按右手法则.天线俯仰轴未转动时，Oa2Za2与天线方位轴重合.单位向量为a2.

1.2 支撑杆柔性振动简化

支撑杆为柔性附件，为了便于分析支撑杆的振动变形，进行等效简化，如图2所示.

图2 支撑杆等效简化

将支撑杆等效为一端固定、一端自由的悬臂梁，将天线等效为质量块，则支撑杆的柔性振动特性可以通过分析自由端带集中质量块的悬臂梁得到.其中悬臂梁的质量为ma1，梁长为L，抗弯刚度为EJ，天线的等效质量为ma2.

对支撑杆进行模态离散，其上任一点的弹性变形位移可以利用模态展开法表示为

ua1(x,t)=Φa1(x)·ηa1(t)

(1)

如果只考虑支撑杆的弯曲变形，则

(2)

选取如下振型：

(3)

式(1)对时间求导得

(4)

1.3 动力学方程

应用拉格朗日建模原理，可得[11]

(5)

式中有关参数意义如下：

ωb——b系相对地球惯性坐标系的角速度；

ωa——Oa2Xa2Ya2Za2相对Oa1Xa1Ya1Za1的角速度；

Ib——卫星相对b系的转动惯量；

Ia——天线相对本体坐标系的转动惯量；

M——支撑杆等效质量矩阵，

Ra——天线转动与卫星姿态运动的刚性耦合系数阵；

Fa——支撑杆振动与卫星姿态运动的耦合系数阵；

Far——支撑杆振动与天线转动的耦合系数阵；

Qb、Qa——分别为驱动姿态运动和天线转动的作用力矩，包括控制力矩和干扰力矩；

Λa1——支撑杆振动固有频率对角阵；

ξa1——支撑杆振动阻尼对角阵.

2 天线运动分析

令θ1和θ2分别表示天线绕方位轴和俯仰轴的转角，如忽略支撑杆端点的变形，并定义天线运动顺序为先方位，后俯仰，则

(6)

进一步求导有

(7)

3 命令预处理

命令预处理(CPP，command preprocessor)是一种指令成型策略，最初应用的目的是为了消除由于实际执行机构速度和加速度限制引起的运动结束后的振动.

CPP的结构如图3所示，其中ri是输入位置信号，即期望的命令或轨迹；rpi是经过预处理后位置信号；ei是预处理位置误差；vi是输入的速度信号；ui是经过预处理后的速度信号；kpi是闭环跟踪控制参数.

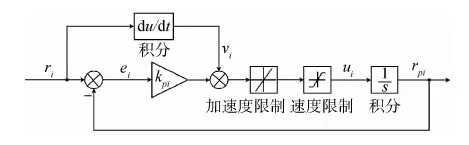
图3 命令预处理算法结构框图

由图3可知，CPP实际上是一个闭环跟踪控制系统.当输入信号的速度和加速度没有超过设定的界限时，闭环控制不起作用，即rpi=ri.而当输入信号的速度和加速度超过设定的界限时，闭环控制系统控制rpi跟踪ri.因此，CPP算法得到的指令情况取决于参数kpi的取值.通常选择非线性形式的kpi，即

kpi=ko+kve-β|ei|

(8)

其中ko为kpi的常值部分，kv为kpi的变化部分的增益，β是指数增益.

由前可知，减小天线运动角速度和角加速度可减小天线运动对卫星姿态运动和支撑杆柔性振动的影响.因此，如果选择合适的角速度和角加速度限制，那么应用CPP算法设计天线回扫指令，能减小天线运动的影响，尤其是回扫结束时的振动.

加入CPP后的天线回扫控制系统如图4所示.

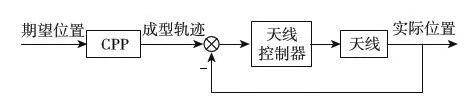
图4 天线回扫控制系统框图

4 仿真分析

用户星为太阳同步轨道卫星，轨道根数为半长轴a=6978km，偏心率e=0.001，倾角i=97.9°，升交点赤经Ω=225.5°，初始幅角us=-136.1°.中继卫星运行在地球同步轨道上，初始幅角为uE=22.8°.

其他参数为

ma1=10kg,L=1.7m,EJ=15000N/m2,ma2=20kg.

为便于分析，只取支撑杆的前两阶柔性振动模态

Λa1=diag{3.318,3.352}Hz

ξa1=diag{0.005,0.005}

卫星姿态控制采用PID控制(控制参数为比例系数P、积分系数I和微分系数D)，天线指向控制系统采用PD控制(控制参数为比例系数P和微分系数D)，参数取值如表1所示.

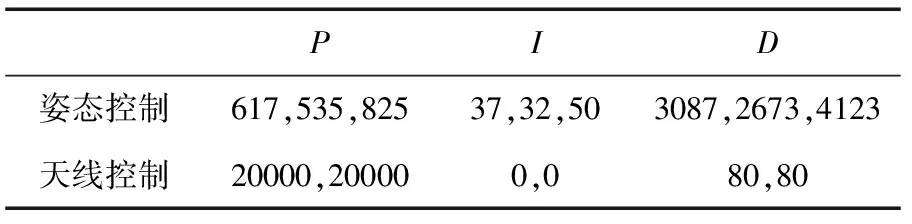
表1 控制参数

CPP取值如下：ko=0.4，kv=2，β=20，速度限制为6(°)/s，加速度限制为2(°)/s2.

假设天线在100s时开始进行回扫，期望的方位角和俯仰角分别为-60°和30°.仿真200s，得到如图5～8所示的仿真结果.

图5～8中实线表示没有采用CPP的仿真结果，虚线表示采用CPP的仿真结果.由图5和图6可知，天线回扫运动对星体姿态角和姿态角速度有较大影响，而CPP环节的引入极大地减小了天线回扫运动对星体姿态稳定的影响.由图8可知，采用CPP对抑制天线柔性振动也有很大的作用，第一阶和第二阶振动模态都从10-4减小到了10-5.CPP环节也带来了一些不好效果，比较明显的是回扫时间变长，如图7所示，方位轴回扫时间从10s增加到了13s，俯仰轴回扫时间从5s增加到了8s.但实际上回扫时间变长并不意味着天线捕获目标时间变长，因为采用CPP后星体姿态和天线柔性振动都得到了有效的改善，将有助于目标的快速捕获.

图5 姿态角曲线

图6 姿态角速度曲线

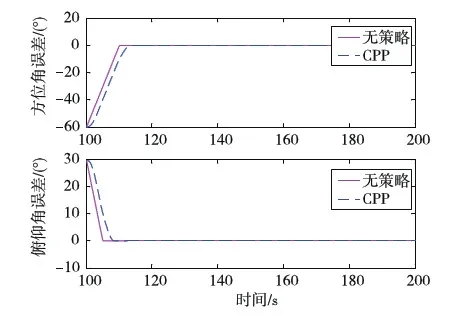
图7 天线回扫角度曲线

图8 天线柔性振动模态

5 结 论

本文针对星间跟踪天线回扫运动过程进行了研究.首先对支撑杆柔性振动进行了等效简化，建立星体姿态运动、天线运动和支撑杆柔性振动的耦合动力学模型.通过分析耦合动力学模型，发现降低天线运动对星体姿态稳定和柔性振动影响的关键是减小天线运动的角速度和角加速度.有鉴于此，引入CPP算法规划天线回扫指令，该算法无需回扫时间等输入，不但可以根据要求限制回扫运动的角速度和角加速度，还对回扫结束后的振动有一定的抑制作用.仿真结果表明天线回扫运动能有效抑制星体姿态稳定和柔性振动的影响，CPP是多体运动耦合的一种有效解决方法.

参 考 文 献

[1]Tham Q, Lee F, Ly J H, et al. Robust antenna pointing control for TDRS spacecraft[C]. The 36thConference on Decision & Control, San Diego, California, USA, 1997

[2]Atluri S N, Atmos A K. Large space structures: dynamics and control[M]. Berlin: Springer-Verlag, 1988

[3]Kane T R, Levinson D A. Dynamics: theory and application[M]. New York: McGraw-Hill, 1985

[4]Leonard M. Hybrid state equations of motion for flexible bodies in term of quasi-coordinates[J]. Journal of Guidance, Control and Dynamics, 1991, 14(5): 1008-1013

[5]齐春子, 吕振铎. 卫星天线跟踪指向控制系统的全系数自适应控制[J]. 航天控制, 1998,16 (3): 1-16

Qi C Z, Lu Z D. All-coefficient adaptive control in the tracking and pointing control system of antenna on satellite[J]. Aerospace Control, 1998, 16(3): 1-16

[6]朱承元, 杨涤, 李顺利. 用户卫星天线跟踪指向自抗扰控制方法[J]. 北京理工大学学报,2006, 26(1): 82-86

Zhu C Y, Yang D, Li S L. Active disturbance rejection method for antenna tracking and pointing control of user-satellite[J]. Transactions of Beijing Institute of Technology, 2006, 26(1): 82-86

[7]吴刚, 张文雅, 何伟平. 中继卫星跟踪航空器的星间天线指向控制算法研究[J]. 飞行器测控学报,2009, 28(6): 23-27

Wu G, Zhang W Y, He W P. The inner orbit linked antenna pointing control algorithm for tracking and data relay satellite tracking aircraft[J]. Journal of Spacecraft TT&C Technology, 2009, 28(6): 23-27

[8]孙小松, 耿云海, 杨涤,等. 中继卫星复合控制系统设计[J]. 飞行力学, 2005, 23(2): 63-66

Sun X S, Geng Y H, Yang D, et al. Design of the complex control system of TDRS[J]. Flight Dynamics, 2005, 23(2): 63-66

[9]Tyler S R. A trajectory preprocessor for antenna pointing[R]. The Telecommunications and Data Acquisition Progress Report, 1994

[10]Gawronski W, Almassy W T. Command preprocessor for radio telescopes and microwave antennas[J]. IEEE Antenna and Propagation Magazine, 2002, 44(2): 30-37

[11]Hu Q L, Shi P, Gao H J. Adaptive variable structure and commanding shaped vibration control of flexible spacecraft[J]. Journal of Guidance, Control and Dynamics, 2007, 30(3): 804-815