一种启发式多标记分类器选择与排序策略

李 哲，王志海，何颖婧，付 彬

(北京交通大学 计算机与信息技术学院，北京 100044)

1 引言

分类是数据挖掘领域中的一个重要分支，它在天气预测、图像识别、贷款风险评估等领域发挥了重要的作用。分类可以分为单标记分类问题和多标记分类问题。

设X表示实例空间，Y表示标记集合，令m=|Y|。在传统的分类问题中，每个实例都只有单个的标记y与之对应，其中y∈Y。训练实例集合D可表示为{(x1, y1), (x2, y2), …, (xn, yn)}，其中xi为D中第i个实例，yi∈Y为与其相关联的标记。当m=2时，这样的分类问题叫二类分类问题；当m>2时，则叫作多类分类问题。无论是二类分类问题还是多类分类问题，都属于单标记分类问题。在多标记分类问题中，每一个实例可能与多个标记相关联，即实例集合D可表示为{(x1, L1), (x2, L2),…,(xn, Ln)}，其中Li⊆Y，为实例xi所关联的一个标记集合。

本文剩余部分组织如下： 第2节总结目前主要的多标记分类方法；第3节重点分析二类转化方法；第4节详细描述了我们提出的算法及与相关算法的比较；在第5节中，我们给出相关实验的设计和实验结果的分析；最后第6节总结本文的工作及其结论。

2 两种多标记分类策略

目前，研究者提出了众多的多标记分类算法，根据文献[1]多标记分类算法可以分为两类： 问题转化方法和算法拓宽方法。前者是将多标记分类问题转化为单个或者多个单标记分类问题[2-4]。后者是通过扩展现有的单标记学习算法，使其能直接处理多标记数据[5]。

2.1 问题转化方法

目前，研究者们提出了众多问题转化的方法，几乎所有这些方法都是基于3种基本的转化策略： 二类转化、复制转化、组合转化[6]。BR(Binary Relevance)方法[2]和CC(Classifier Chain)方法[3]是两种典型的基于二类转化的方法，它们都是将一个多标记分类问题转化为m个二类分类问题，后者通过对前者的改进，将标记间的依赖关系考虑进算法中，从而能够获得更好的分类效果。另两种经典的多标记分类算法是LP(Label Powerset)方法[7]和RAkEL(RAndom k-labELsets)方法[4]，它们都是基于组合转化策略，前者将所有的标记看成一个整体，而后者先将标记集合分为若干个子集合，再将每个子集合看成一个整体。

2.2 算法拓宽方法

算法拓宽方法(C4.5)是单标记分类中一个经典的算法，Clare等人通过修改C4.5中熵的计算公式，使其能够处理多标记数据[1]。修改后的熵计算公式如式(1)所示。

其中，p(ci)表示标记ci出现的概率，q(ci)=1-p(ci)且ci∈Y。Clare等人使用修改后的熵来计算决策树在某个属性上分裂时的信息增益，从而决定分裂属性并构建完整的决策树。在这个算法中，决策树的叶子节点可能是多个标记的集合。此外，ML-kNN、Adaboost.MH等也是基于算法拓宽的多标记分类算法[5]。

3 二类转化方法

在3种基本的转化策略当中，二类转化是运用最为广泛的方法，该方法的核心思想就是将一个多标记分类问题转化为m个二类分类问题，其中最关键的一步就是将多标记数据集D转化为m个单标记数据集。事实上，对于第i个转化后的数据集Di，我们无非要解决两个问题：一是确定这个数据集的特征集合Ai，二是确定该数据集的类属性对应的标记bi。因此，二类转化方法的核心就是找到某种方法来确定相应的Ai和bi，其中i=1, 2,…, m。

BR是最简单的基于二类转化方法的多标记分类算法，在BR中，所有Ai都是数据集的原始特征集合，BR算法最大的缺点在于其没有考虑标记间的依赖关系。研究者们提出了在原始特征集合中加入某些标记对应的0/1属性的方法，使算法能够利用标记间的依赖关系，比如BR+算法[8]，CC方法[3]，BCC算法[9]等。

本文提出了一种基于二类转化方法的多标记分类算法，在我们的转化方法当中，在选择特征集合Ai时，我们采用的是依次递增的方式。这样做的好处是能够尽可能地将更多的标记对应的0/1属性加入特征集合来充分利用标记间的依赖关系，同时也使得构建的m个单标记分类器组成一种链式结构，从而算法能够在预测阶段有序地进行。在确定了Ai后，该算法采用某种搜索策略来选择相应的bi。

4 有序分类器链算法

本节详细介绍我们提出的算法，该算法的具体训练过程在4.2节中给出，4.3节对该算法和传统的分类器链算法进行比较分析。

4.1 提出算法的动机

对于一个训练集中的一个实例(x, L)，其中L⊆Y可以用一个向量(l1, l2, …, lm)∈{0, 1}m来表示，li=1说明标记yi与实例x关联。在给定一个实例x时，一种标记组合L=(l1, l2, …, lm)，在x条件下的条件概率可用概率的乘法法则来计算，如式(2)所示。

一个多标记分类模型的目的就是要找出使得式(2)值最大时的标记组合L，然而在标记集合Y下，所有可能的标记组合数目为2m。这2m种标记组合可以用一棵二叉树来表示，那么一条从根节点到叶子节点的路径就是一种可能的标记组合。显然，搜索这全部2m条路径的代价会很大。对于这个问题，所有基于二类转化方法的算法似乎采取了一种折中的方式。这些算法得到的一个分类器集合C1, C2, …, Cm，其中Ci的任务就是找出使得P(li| x, l1, …, li-1)值最大时li的取值(1≤i≤m)。不难看出，这个分类器集合C1, C2, …, Cm依次找到了式(2)中第i个相乘项在局部条件下得到最大值时li的值。显然这并不能保证这m个项的乘积是所有2m个标记组合中最大的，这相当于在之前提到了那棵二叉树中搜索了仅仅一条路径(每次都选择当前节点上更好的分支往下走)。然而，这种局部最优的算法能够得到令人满意的分类精度，同时保持可以接受的计算复杂度。

我们注意到，在式(2)中标记的顺序是一个影响分类结果的重要因素。给定标记集合Y={y1, y2, …, ym}，当标记顺序为y1′→y2′→…→ym′时，则标记组合L可以用一个向量(l1′, l2′, …, lm′)∈{0, 1}m来表示，li′=1说明标记yi′即标记顺序中第i个标记与实例关联，此时，式(2)可以写成式(3)的形式。

显然，对于不同的标记顺序，式(3)的计算结果必然也不一样，从而得出不同的分类结果。对于标记集合Y，所有可能的标记顺序的数目为m!，显然要想考虑所有这些情况是不现实的。那么，如何找到一种合适的标记顺序，也即是如何依次确定yi′(1≤i≤m)，同时又避免过大的计算开销，这对于提高分类器性能就显得尤为重要。前面介绍过，基于二类转化的算法在找出使得式(2)值最大时的标记组合L时采取了一种局部搜索的策略。受到这个的启发，我们使用了一种类似的搜索策略，通过依次选择使得第i个相乘项对应分类器效果最好的yi′，从而确定一种标记顺序来构建分类器，该算法的具体过程将在下一节中介绍。

4.2 算法的过程

在我们提出的算法中，在选择特征集合Ai时，我们采用的是依次递增的方式。A1是训练集的原始特征集合，对于所有的i > 1，Ai是在Ai-1的基础上多加了一个属性。这样做的好处是能够将尽可能多标记对应的0/1属性加入特征集合来充分利用标记间的依赖关系，同时也使得构建的m个单标记分类器组成一种链式结构，从而算法能够在预测阶段有序地进行。在确定了Ai后，该算法在选择相应的bi时，采用了搜索的策略，在所有可能的标记中，选择了使得对应分类器效果最好的一个。这个算法的训练过程预测过程分别如图1和图2所示。

01.输入:D={(x1,L1),(x2,L2),…,(xn,Ln)}02.A={}03.fork=1to|Y|04. B={}05. foreachyi∉A(Yi∈Y-A)06. D'={}07. forj=1ton08. D'=D'∪((xj,l1',…,lk-1'),li)09. end10. TrainCi:D'→li∈{0,1}11. 计算并保存分类器Ci的分类准确率(采用5重交叉验证)12. B=B∪{Ci}13. end14. 选择B中评价结果最好的分类器Cx(1≤x≤|B|)15. yk'=yx,Ck'=Cx,A=A∪{yx}16.end17.输出:链式分类器集合C1',C2',…,C|Y|'图1 算法的训练过程

01.输入:待分类实例x,链式分类器集合C1',C2',…,C|Y|'02.L={}03.forj=1to|Y|04. L=L∪(lj←Cj':(xi,l1,…,lj-1))05.end06.输出:对x的分类结果L图2 算法的预测过程

从图1中可以看出，算法通过m(即图1和图2中的|Y|)次循环，依次训练出m个单标记分类器。根据标记是否被选择作为某个bi，算法将所有标记分为已选择的和未选择的两个集合(分别地应于图1中的A和Y-A)。在第i次循环中，我们将已选择的i-1个标记对应的0/1属性加入到训练集的特征集合中，也就是确定了Ai。再分别把未排序的m-i个标记作为bi，在这些新的数据集上训练出二类分类器并评价它们，然后从这m-i个分类器中选择分类性能最好的一个作为第i个分类器，同时我们就确定了bi并将该标记加入已选择的标记集合。我们在比较分类器时，用的是分类准确率作为评价标准，并采用5-重交叉验证的方式。如图2，在算法的预测过程中，按照训练时的顺序依次选择分类器Cj′为待分类实例分类，最后将m个分类结果组合起来作为多标记分类结果输出。

4.3 与传统分类器链的比较

可以看到，我们提出的算法与Read等人提出的CC算法相似，构建的多标记分类器都是由m个链式结构的二类分类器组成。进一步分析可以得出，我们的算法实际上通过启发式的搜索策略找到了一种合适的顺序来构建分类器链，因此我们将这个算法叫做有序分类器链(Ordered Classifier Chain)方法，简称OCC算法。

在文献[3]中，作者提到了分类器链自身的顺序必然会对分类结果产生影响。分类器链的顺序反映了标记间不同的依赖关系，各个数据集中标记间的依赖关系是不一样的，因此有必要找到更加合适的分类器链顺序，用来更好地考虑标记间的依赖关系。然而CC算法中并没有提供选择标记顺序的方法，它使用的是随机的顺序，这有可能降低算法的分类效果。在文献[3]中，作者提出了ECC方法，它是由若干个随机顺序的分类器链组成的组合分类器，它的分类结果由这些分类器链通过投票的方式决定，其目的就是为了减少仅使用一种随机顺序的分类器链可能给分类带来的负面影响。

OCC算法的目的就是要找出使得式(3)值最大时的标记组合L，在式(3)中，第i个相乘项对应于分类器链中的第i个分类器，它的值就是由其对应的分类器计算而来。因此，不同的分类器链顺序必然导致计算式(3)时的不同结果。OCC算法正是从式(3)入手来选择一种分类器链顺序，在OCC中，依次选择了使得第i个相乘项对应分类器效果最好的yi′。

我们可以用如图3所示的一棵树来表示所有可能的标记顺序，除根节点以外的所有节点都对应着一个标记和一个二类分类器，这个分类器是通过把当前节点的所有祖先节点对应分类器的类属性加入到原始特征集合后再训练而来，它的类属性就是该节点对应的标记。因此从根节点到叶子节点的任意一条路径对应着一种可能的标记顺序，也即是分类器链的顺序。OCC算法在每个节点上总是选择对应分类器准确率最高的子节点，从而找出一条完整的路径，最终选择出了一种分类器链顺序。可以看出，OCC算法采用的是局部最优的搜索策略，这不仅能够得到较好的结果，同时能够避免搜索全局空间带来的过大计算开销。

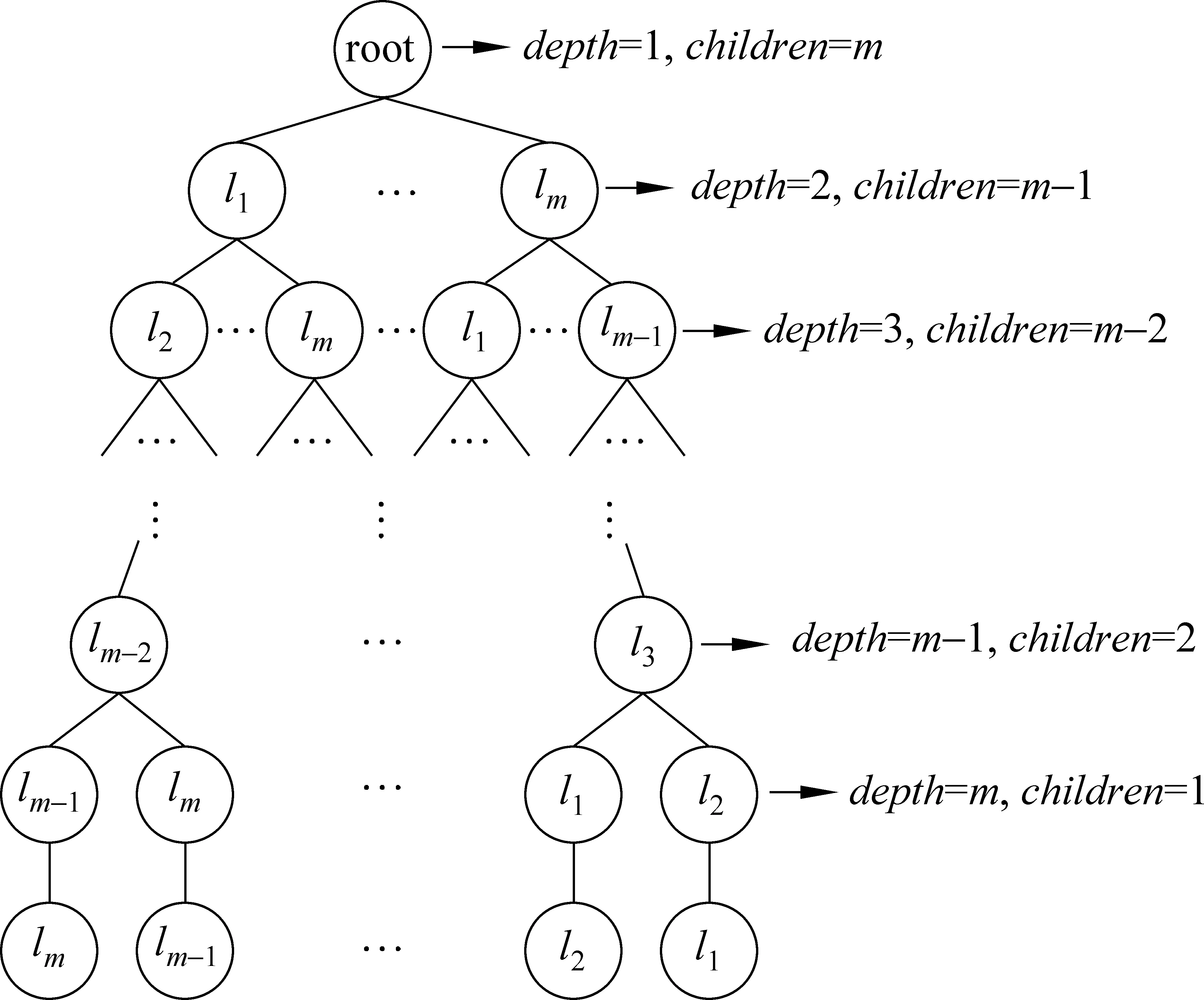
图3 表示所有m!种标记顺序的树注： depth表示节点深度，children表示子节点个数

OCC算法通过启发式的方法找到了一种标记顺序来构建分类器链，搜索的过程必然导致OCC算法将比CC算法消耗更多的时间。不难得出，在CC算法的训练阶段总共需要训练m个基分类器来构建分类器链。在OCC算法的训练阶段，在m次循环的第i次中，需要比较m-i个基分类器的性能，由于我们采用的是5-重交出验证的方式，因此在这次循环中需要训练的基分类器的个数是5(m-i)，则OCC算法中需要训练的基分类器的个数是5(m+1)·m/2。可以看出，OCC算法训练阶段所要的时间是CC算法的(5m+5)/2倍。若所选基分类器在训练阶段的时间复杂度为O(n)，则CC算法和OCC算法在训练阶段的时间复杂度分别是O(mn)和O(m2n)。而在预测阶段，这两个算法的时间复杂度是一样的。

5 实验

在5.1和5.2节中，我们分别介绍实验中用到的评价指标和对比算法。

5.1 评价指标

Hamming损失是多标记分类问题中较为常见的一个评价指标，其计算如式(4)所示，其中L和C分别表示实例x相关联的标记集合和分类器为x预测的标记集合，m是所有标记的个数，⊕是两个集合的对称差运算。

不难看出，Hamming损失表示的是在标记集合Y中被错误地预测的标记的个数。事实上，它可以写成如式(5)所示的传统二类分类问题当中的0/1损失函数的和的形式，其中Loss(Li, hi(x))是对应于分类器链中第i个分类器的0/1损失函数。第3节中讨论过了，OCC算法是依次找到在局部条件下最好的分类器，因此OCC算法在局部空间上搜索到使得Hamming损失尽可能小的模型。

子集损失(Subset 0/1 Loss)是多标记分类问题中另一种损失函数，其计算公式如式(6)，其中，I(true)=1，I(false)=0。比起Hamming损失，子集损失更能够反映出分类器对标记之间依赖关系的关心程度[10]。考虑到OCC算法最初就是为了改进CC算法找到一种标记顺序从而更好地挖掘标记间的依赖关系而启发的，因此我们在实验中选用了子集准确率(Subset Accuracy)评价指标来对OCC算法的有效性进行评价(子集准确率=1-子集损失)。

此外，我们还用到了覆盖值(Coverage)和Micor-F1测量值，前者是一种基于输出结果为标记序列的评价指标，后者是一种将F1测量值应用到多标记分类中的评价指标[7]。

5.2 算法和数据集

我们在试验中选取了4种常见的基于问题转化方法的多标记分类算法与本文提出的OCC算法进行对比： BR(Binary Relevance)，CC(Classifier Chain)，ECC(Ensembles of Classifier Chain)和RAkEL(RAndomk-labELsets)。我们在Mulan平台下实现了OCC算法，Mulan是一个基于Weka的开源多标记实验平台。其他的几个算法都是使用Mulan中自带的程序，ECC算法中分类器链的个数设定为10，RAkEL算法中标记子集合的大小k设定为3，所有算法中使用的基分类器均是NaiveBayes分类器，其他未说明的参数均使用的是Weka和Mulan中程序的默认参数。

实验中使用的数据集是来自不同领域的7个多标记分类问题标准测试集*这些数据集均是从网站http://mulan.sourceforge.net/datasets.html下载．，如表1所示。表中列出了数据集的名称、领域、实例个数、属性个数和标记个数。可以看到，这7个数据集来自本文、音乐、生物和图像四个不同的领域，它们的实例个数从几百至几万不等，标记个数从6至153不等。数据集medical是有关医学自然语言处理的数据，每一条实例是利用1 449个关键字对一个病人症状文本描述的特征向量表示，特征属性对应于1 449个关键字，标记对应于45个保险种类。emotions是一个关于音乐情感分类的数据集，研究人员对总共233首音乐作品分别提取了30秒的片段，再从这些片段中抽取了若干样本，从每个样本中提取了72个特征属性，这些特征属性可以分为与节奏相关和与音色相关的两大类别，6个标记则对应于6种不同的情感。所有这些数据集的详细描述和属性说明都能通过我们给出的链接找到。

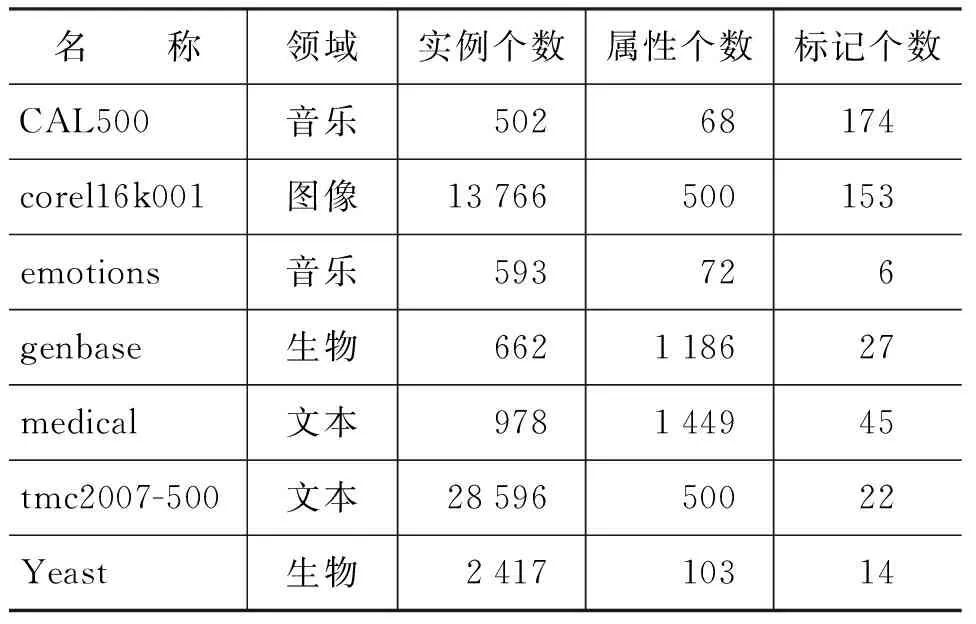
表1 实验中使用的数据集

对于数据集CAL500，emotions，genbase，medical，tmc2007-500和yeast，我们都采用了10-重交叉验证的方式，记录4个评价指标在10-重交叉验证下的平均值。而对于core116k001数据集，由于它的实例个数和标记个数都比较大，我们将它分为训练数据和测试数据两部分，前者用来训练分类器，后者用来测试。

5.3 结果和分析

表3列出了本文提出的OCC算法和其他4个经典算法在数据集上各个评价指标的测试结果，其中黑体表示的是某一数据集上表现最好的算法，括号中的数字表示的是该算法的排名值，这5个算法在各个评价指标上的平均排名值如表2所示。

表2 算法的平均排名值

对于Hamming损失评价指标，从表3中可以看出，OCC算法在Hamming损失上表现得很好，在7个数据集中的6个都取得了第一名，并且对比其他几个算法优势也比较明显，同时在表2中，它的平均排名结果也要好于其他4个算法。从对OCC算法构建分类器的过程和本节中对式(5)的分析来看，OCC算法在这个评价指标上的优势是意料之中的。

表3 所有7个数据集上的实验结果

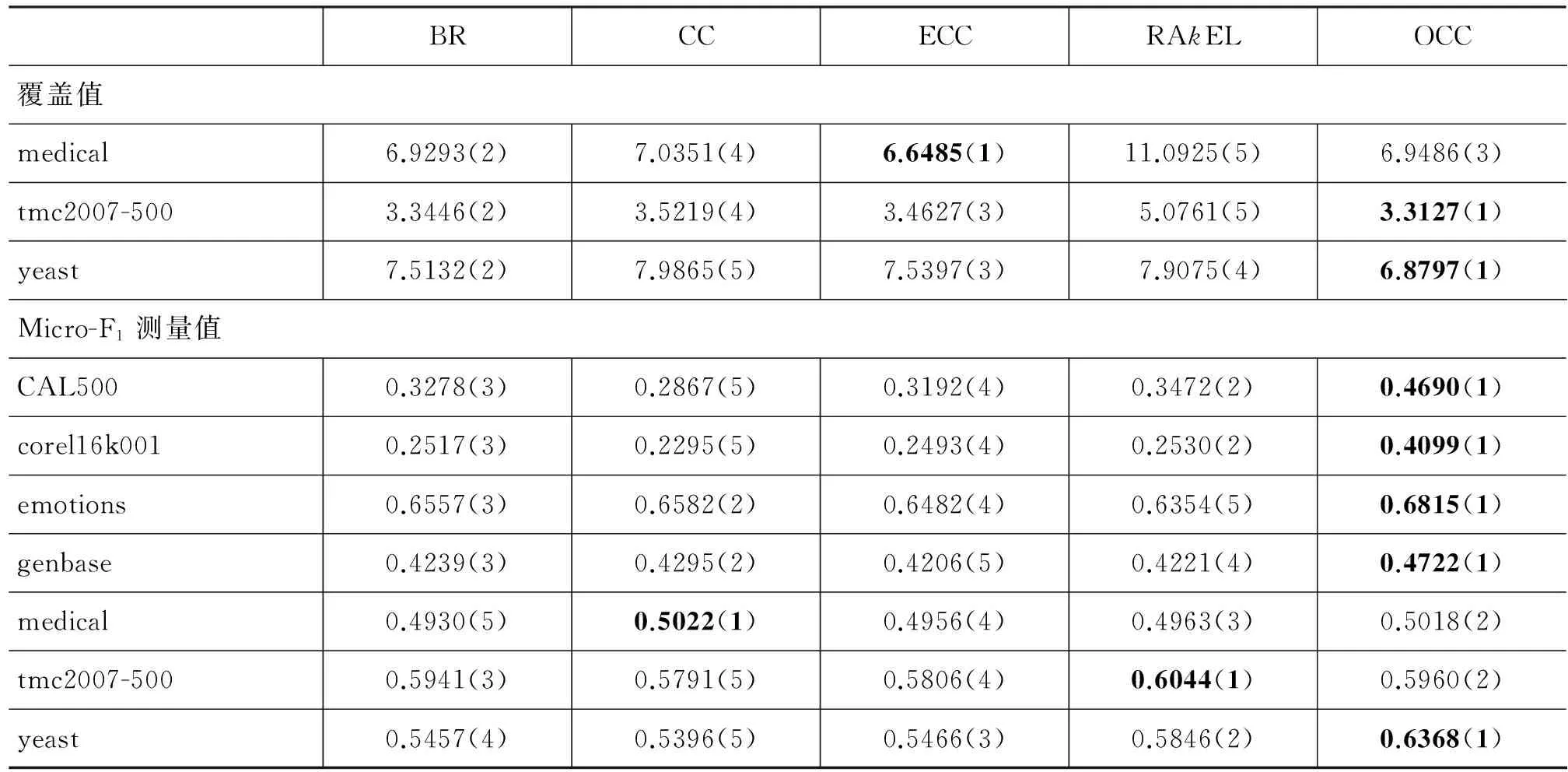
续表

对于子集准确率评价指标，OCC算法虽然不像Hamming损失指标那样在绝大部分数据集上都有压倒性的优势，它在3个数据集上的效果最好，同时在其他的数据集上的排名也相对靠前。在表2中，子集准确率上的平均排名值也是最好的，因此，说明OCC算法通过找到一种尽可能好的标记顺序构建分类器链，更加充分地利用标记间的依赖关系来提升分类效果，而BR算法由于没有考虑标记间的依赖关系，在子集准确率上的平均表现最差。同时CC和ECC算法比RAkEL取得了更好的结果。

在OCC算法中，我们并没有刻意地去改进分类器对标记排序的输出结果，然而从表2可以看出它仍然在覆盖值上取得了最好的结果，虽然比起ECC算法，这个优势是很微弱的，从表3中也可以看到，OCC和ECC分别在4个和3个数据集上取得了最好的结果。这两个算法在覆盖值上的结果要好于其他两个算法。

对于Micro-F1指标，表3显示OCC算法在5个数据集上得到了最好的结果，并且在这5个数据集上OCC比其他4个算法的结果都有较大地提高，而在另外两个数据集上，OCC亦是排在第2。表2也说明了OCC在Micro-F1上的优势是显著的。

6 结论

在本文中，我们提出了一种基于问题转化方法的多标记分类算法。该算法通过启发式方法搜索出一种合适的标记顺序，从而构建出一个有序的分类器集合。我们从理论上分析了该算法通过这种搜索策略，能够获得比典型的多标记分类算法更加好的分类效果。同时，我们也给出了算法时间复杂度的对比，虽然我们的算法复杂度比所对比的算法要高，但这个消耗是可以接受的。

我们将OCC算法与其他4个常见的多标记分类算法在来自不同领域的7个数据集上进行对比实验，实验中使用了多种评价指标。实验结果说明我们提出的算法在所有4个评价指标上都取得了最好的平均结果，尤其在Hamming损失和Micro-F1评价指标上有明显的优势。该算法在子集准确率评价指标上的结果说明它能够更好地利用标记间的依赖关系。此外，我们的算法虽然没有刻意改进基于标记排序的输出结果，但仍然在基于标记排序的评价指标覆盖值上取得了较好的结果。

[1] Tsoumakas G, and Katakis I. Multi-Label Classification: An Overview[J]. International Journal of Data Warehousing and Mining, 2007，3(1)： 1-13.

[2] Boutell M R, Luo J, and Shen X， et al. Learning multi-label scene classification[J]. Pattern Recognition, 2004, 9(37): 1757-1771.

[3] Read J, Pfahringer B, and Holmes G， et al. Classifier chains for multi-label classification[C]//Proceedings of the 2009 European Conference on Machine Learning and Knowledge Discovery in Databases: Part II. Bled, Slovenia, 2009: 254-269.

[4] Tsoumakas G, Katakis I, and Vlahavas I. Random k-labelsets for multi-label classification[J]. IEEE Transactions On Knowledge and Data Engineering, 2010, 23(7): 1079-1089.

[5] Zhang M, and Zhou Z. A k-nearest neighbor based algorithm for multi-label classification[C]//Proceedings of the 1st IEEE International Conference on Granular Computing. Beijing, China, 2005: 718-721.

[6] Read J. A pruned problem transformation method for multi-label classification[C]//Proceedings of the NZ Computer Science Research Student Conference. Christchurch, New Zealand, 2008: 143-150.

[7] Tsoumakas G, Katakis I, and Vlahavas I. Mining multi-label data[M]. Maimon O, and Rokach L. (eds.). Data Mining and Knowledge Discovery Handbook, 2nd Edition. Springer, 2010: 667-685.

[8] Cherman E A, Metz J, and Monard M C. Incorporating label dependency into the binary relevance framework for multi-label classification[J]. Expert Systems with Applications. 2011.

[9] Zaragoza J H, and Sucar L E. Bayesian chain classifiers for multidimensional classification[C]//Proceedings of the 22nd International Joint Conference on Artificial Intelligence. Barcelona, Spain, 2011: 2192-2197.

[10] Dembczynski K, Waegeman W, and Cheng W. Regret Analysis for Performance Metrics in Multi-Label Classification: The Case of Hamming and Subset Zero-One Loss[C]//Proceedings of the 2010 European Conference on Machine Learning and Knowledge Discovery in Databases. Barcelona, Spain, 2010: 280-295.