实数集到时标上的概念推广的若干原则
2023-01-14赵莉莉
赵莉莉
(云南大学 数学与统计学院, 昆明 650091)
1 引 言
微分方程与差分方程在理论与实际应用上具有相同的研究价值,探究微分方程与差分方程解的存在性与唯一性一直是研究热点,取得了不少的研究成果[1-3], 但是分别研究这两类方程又会在无形之中加大工作量,时标理论很好地解决了这一问题,它能将两者有机地统一起来,只需将实数集上的概念推广到时标上,建立时标上相应的理论,当时标退化为实数集和整数集时,所得到的理论就分别是微分方程和差分方程中的理论.因此,将实数集上的概念推广到时标上是有意义的.
2 遵循的原则
如果将定义在实数集上的某类函数推广到了时标上,但在时标上却找不到这种函数的例子,那该定义的推广就是毫无意义的,所以,从实数集到时标上的概念推广,第一个应该遵循的原则是—推广后的概念是良定义.
2.1 良定义
在笔者的以前的论文中[4]已经将加权伪概周期函数的概念推广到了时标上,并在时标上讨论了这类函数的一系列性质,得到了时标上一阶动力方程的加权伪概周期解的存在性定理,使得在时标上探讨动力系统的加权伪概周期解的存在性成为了可能,为了佐证所推广的定义是合理的,本文将给出时标上加权伪概周期函数的例子.
定义1[5]实数集的任意一个非空闭子集称为一个时标.称时标T是一个概周期时标,是指Π∶={r∈∶t±r∈T,∀t∈T}≠{0}.
注1 容易看出0∈Π,即Π并非空集,故由定义1可得:称时标T是一个概周期时标,是指∃r≠0,使得对于每一个t∈T,都有t±r∈T成立.
定义2[4]称u∶T→[0,+∞)是一个权函数,是指u在T上局部可积,且几乎处处为正.用U表示时标上全体权函数构成的集合.
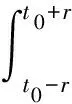
定义3[4]设u∈U∞.称一个连续函数f∶T→n是加权伪概周期函数,是指:f可以表示为f=φ+ψ,其中φ∈AP(T,n)是一个概周期函数,而ψ∈PAP0(T,n,u).定义函数空间PAP0(T,n,u)如下:
从T映射到n的全体加权伪概周期函数构成的集合用PAP(T,n,u)表示.定义3将加权伪概周期函数的概念从实数集上推广到了时标上.
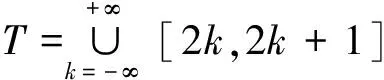
令h(t)=sin(πt)e-|t|,则h(t)∈BC(T,).由

可得
从而
即h(t)=sin(πt)e-|t|∈PAP0(T,,u),再考虑到g(t)=cos(πt)是该时标上的概周期函数,所以
f(t)=cos(πt)+sin(πt)e-|t|∈PAP(T,,u).
2.2 一致性
实数集是时标的特例,将实数集上的概念推广到时标上之后,当时标退化为实数集时,所得到的概念应该与实数集上的概念一致.
在本小节中, 将以全局指数稳定性为例进行探讨.在时标上讨论如下的一阶微分方程组
(1)
其中系统(1)的初值为
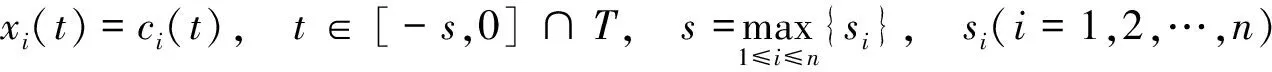
近几年来,关于时标上各类微分系统的各类解函数的全局指数稳定性的研究,已经取得了不少的成果[6-8].若用这些文献中所采用的方法, 定义系统(1)解函数的全局指数稳定性,其定义如下.
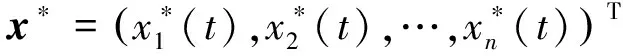
其中
当时标退化成实数集时,定义4相应地退化为定义5.
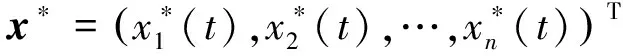
其中
但是实数集上全局指数稳定的定义[9-11], 应是定义6.
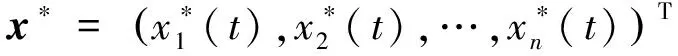
其中
显然,对于每一个δ∈[-s,0],都有e-λ(t-δ)≤e-λt成立,反之却不一定成立,即定义5比定义6强,这是不合理的,不妨修改定义4如下.
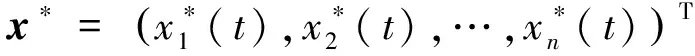
其中
当时标退化为实数集时,定义7也就退化成了定义6.采用定义7的方法,也可以定义时标上其它微分系统解函数的全局指数稳定性.
3 继承性
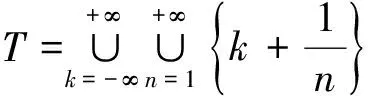
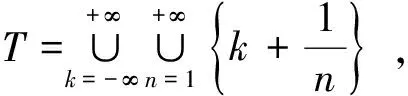
首先证明Π=.由时标的构造,易得⊂Π.∀r∈Π,因为0∈T,所以r∈T,即Π中的每一个常数都可以表示成的形式,其中k是一个整数,n是一个正整数.现证明n只能取1,即Π⊂.若不然,因为⊂Π,且Π关于实数的加法与减法都是封闭的,所以∃n0≥2,使得又考虑到从而再考虑到由时标的构造,存在正整数n1,使得即又因为所以再考虑到n1≠1,否则又因为所以由时标的构造,这是不可能的,从而再次由时标的构造可得存在正整数n2,n3,使得从而即n2+n3=n2n3,由上式可得n2,n3不能同为奇数,也不可能一个是奇数一个是偶数,只可能同为偶数.所以存在正整数k1,使得即但是矛盾,故n只能取1,即Π⊂,从而Π=.
若f(t)=sint为T上的周期函数,则∃k0>0,k0∈=Π,使得∀t∈T,有sin(t+k0)=sint成立.因为1-k0∈T,所以
sin1=sin(1-k0+k0)=sin(1-k0).
(2)
又因为-1-k0∈T,所以
-sin1=sin(-1)=sin(-1-k0+k0)=sin(-1-k0)=-sin(1+k0).
即
sin1=sin(1+k0).
(3)
由(2)式与(3)式可得:sin(1-k0)=sin(1+k0),即cos1sink0=0,也就是sink0=0.又考虑到,找不到l0∈,使得k0=l0π,故sink0≠0,矛盾,从而f(t)=sint不是T上的周期函数.
4 结 论
时标理论不仅能将微分系统与差分系统有机地统一起来,它还能涵盖许多混合型系统,在理论与实际应用上都具有极强的价值,因此将实数集上的概念推广到时标上,建立时标上相应的理论是有意义的.首先,将实数集上的概念推广到时标上,必须保证推广后的定义是良定义,否则这样的推广是毫无意义的; 其次,推广到时标上的定义,当时标退化为实数集时,应与实数集上的定义一致,只有这样,在时标上获得的结论,才能涵盖在实数集上已经获得的结论,推广的定义才是有价值的.函数是微积分学的主要研究对象,而要深刻认识一个函数,必须了解它的几何性质,因此,考虑定义在实数集上函数的几何性质,能否被时标继承下来也是有意义的.实数集上函数的单调性、有界性都能被时标继承下来,但奇偶性与周期性却不一定能被时标继承下来.
致谢作者非常感谢参考文献对本文的启发以及审稿专家提出的宝贵意见.
