碳纳米锥力学特性的分子动力学研究*

李明林 林凡 陈越

(福州大学机械工程及自动化学院，福州 350108)

(2012年6月6日收到;2012年8月6日收到修改稿)

1 引言

自从1991年Iijima[1]发现碳纳米管以来，各种碳纳米结构吸引了众多科技工作者的广泛关注和深入研究，包括碳纳米管[2]、石墨烯[3]、碳纳米锥[4]等.这主要是因为这些碳纳米结构存在着诸多奇特且异常显著的物理化学性能，如高强度、低密度、高导电率、高导热率和大的比表面积等特性.基于这些卓著的物理化学性能，这些碳纳米结构在各个工程领域存在着广泛而巨大的应用潜力，例如纳米机电系统[5].碳纳米管和石墨烯由于其在制备能力方面所取得的突破性进展而较早受到广泛而深入的研究.紧随其后的是碳纳米锥由于其独特的锥形结构正受到越来越多的科技工作者的关注.

碳纳米锥的研究最早见于1994年Ge和Sattler[6]对其结构的预测.随后，Krishnan等[7]通过实验证实碳纳米锥存在5种锥角.而Iijima等[8]在1999年将单壁碳纳米锥的每小时产量提高到了10 g.随着对碳纳米锥制备方法的成功掌握，其热学[9]、电学[10]和力学[11]特性的研究也逐渐铺展开来.然而，至今针对碳纳米锥力学特性的研究文献尚不多见.2004年Wei和Srivastava[12]通过连续介质弹性理论和分子动力学模拟推测出单壁碳纳米锥的杨氏模量为其等价碳纳米管的cos4θ.同年，Jordan和Crespi[13]利用分子动力学模拟发现碳纳米锥的封闭顶部受球体缓慢挤压后不发生化学键的断裂，而是发生完美的手性翻转.这类似于“翻口袋”现象，即锥体的外表面变为内表面，而内表面翻转为外表面.2007年，Tsai和Fang[14]利用同样的方法研究显示碳纳米锥的锥角越大，其结构越稳定.同年，Wei等[15]通过分子动力学模拟研究等长度的单壁碳纳米锥的拉伸弹性和塑性特性.研究结果显示，锥角越大，碳纳米锥的弹性应变极限越小，而其断裂强度则越大.由此，他们得出锥角为零的等长度碳纳米管具有最小的断裂强度和最大的弹性应变极限.同年，Liew等[16]则通过分子动力学模拟研究单壁碳纳米锥台的受压曲屈行为.研究结果显示，锥台的高度与底半径之比固定的情况下，锥顶半径越小其刚度越大.2012年，Firouz-Abadi等[17]通过分子动力学模拟研究悬壁的单壁碳纳米锥的横向共振特性.其研究结果表明，一般情况下旋转位移角度(disclination angle)和锥高越小其共振频率越大，但240°角除外.此外，研究也显示悬臂的单壁碳纳米锥的共振频率几乎不受环境温度的影响.

目前国内针对碳纳米锥的研究虽然也取得了一些有价值的成果，但关于碳纳米锥的力学特性分析却少有报道.2007年沈海军等[18]基于Brenner势分子动力学模拟方法研究平板与碳纳米锥作用过程的能量、力和构形的演化.本文针对由相当数量或质量的碳原子所组成的各种锥角和长度不等的碳纳米锥和碳纳米管，通过经典分子动力学模拟方法，研究其在恒温条件下的拉压力学行为，以期获得较为完整的拉压载荷-应变关系曲线及其承载能力.

图1 碳纳米结构图 (a)碳纳米锥;(b)碳纳米管

2 模型和模拟方法

碳纳米锥和碳纳米管的结构如图1所示.本文主要研究由约580个碳原子组成的4组碳纳米锥：(112.88°，1.33 nm)C1，(83.62°，2.0 nm)C2，(60.0°，2.68 nm)C3，(38.94°，3.57 nm)C4，括号内分别表示锥角α和锥高h.与碳纳米锥形成对照组的碳纳米管为4.0 nm长的(15，0)单壁碳纳米管(carbon nanotube，CNT).这些纳米结构的碳原子数分别为580，580，576，576，576.随着锥角的减小，碳纳米锥的锥顶原子的个数分别为5，4，3，2.

本文模拟采用大规模原子/分子并行模拟器(large-scale atomic/molecular massively parallel simulator，LAMMPS[19])的经典分子动力学模拟方法.经典分子动力学本质上是一种粒子方法，因其求解对象是基于牛顿第二定律的粒子动力学控制方程，即

其中，mi和ri分别表示第i个粒子的质量和空间位置，V是系统的经验作用势，而∇表示空间梯度.对粒子位置和速度的积分运算采用Verlet方法.碳纳米结构的原子间相互作用势通常采用Brenner半经验势，也叫Tersoff-Brenner势[20].Brenner势是对Tersoff势的进一步修正，使之能更恰当地反映C—C化学键的形成和断裂过程，已成功用于预测和验证碳纳米结构的各种力学特性.由于第二代Brenner势 (reactive empirical bond order potential，REBO势)[21]主要考虑原子间的短程相互作用，本文增加了考虑原子间长程相互作用的Lennard-Jones势，即

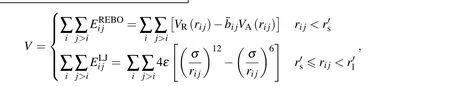
其中，rs和rl分别表示短程作用势和长程作用势的截断半径，分别取值0.2 nm和0.85 nm;VR和VA分别表示短程作用势的斥力项和引力项，bij是原子间的反应经验键序;ε和σ分别是一对原子间的平衡势能和平衡距离，对C—C原子而言，ε=4.2038×10-3eV，σ=0.34 nm[22].

考虑到纳米结构受拉/压过程的准静载恒温条件，以及连续的加载和力学响应过程，本文对碳纳米结构力学特性的分子动力学模拟实验步骤如下：1)固定碳纳米结构底部2层原子，并通过共轭梯度法对此结构进行能量最小化，能量优化指标为10-10eV，力优化指标为10-10eV/˚A，随后通过10 ps的趋衡模拟，使其达到恒温条件下的平衡;2)针对碳纳米锥和碳纳米管的轴向拉伸，均采用逐步定向移动其自由端2层原子，并每隔1000步记录此2层原子所受合力的轴向分量，由于横截面的应力沿轴向位置变化，本文主要统计轴向载荷-轴向应变关系曲线;3)针对碳纳米锥和纳米管的轴向压缩，均采用逐步移动刚性石墨烯平板进行压缩.轴向载荷以平板所受合力的轴向分量表示.系统环境温度采用Berendsen温控方法进行恒温控制，其指数衰减系数为0.1 ps.

为确定合适的模拟时间步长、拉压速率和环境温度，首先在较低的温度(0.1 K)和加载速率 (0.001 nm/ps)条件下，分别采用 0.1，0.2，0.5，0.8和1.0 fs时间步长观察碳纳米锥C2的拉伸载荷-应变曲线.模拟结果表明，时间步长越大，C2的受拉载荷极限和应变极限越小.在0.1，0.2和0.5 fs下载荷极限均值约为279.66 nN(相对偏差低于0.6%)，载荷单位由实验的eV/˚A变换为nN(1 eV/˚A≈1.602 nN).在0.8和1.0 fs下载荷极限约为208.26 nN(与0.5fs相差达约25%).因此，后续模拟的时间步长均采用0.5 fs.紧接着，在0.1 K温度和0.5 fs步长条件下，分别取用0.0005，0.001，0.003，0.005，0.007，0.01，0.02，0.05，0.07 和 0.1 nm/ps速率拉伸C2.结果表明，拉伸载荷极限随着拉伸速率的增加而减小.在[0.0005，0.01］nm/ps范围，载荷极限的均值约为278.88 nN(相对偏差低于0.5%);当拉伸速率大于0.02 nm/ps时，载荷极限偏离上述均值均大于2.5%.因此，综合考虑模拟精度和时间消耗，后续模拟均采用0.01 nm/ps的加载速率.最后，在0.5 fs时间步长和0.01 nm/ps加载速率条件下，分别观察 0.1，1，10，30，100，300 和 500 K 温度下 C2 的拉伸载荷极限.结果表明，随着温度升高，拉伸载荷极限均出现不同程度的降低.在[0.1，10］K低温区间，载荷极限的均值约为276.88 nN(相对偏差低于0.7%).在[30，500］K区间，载荷极限加速降低至最低158.3 nN.从30 K起，载荷极限已偏离低温均值约13.2%至240.3 nN.虽然载荷极限在0.1至10 K的低温环境变化不大，但温度升高时热扰动对载荷-应变曲线的影响渐趋明显.因此，为减少热扰动对结构本征力学性能的影响，后续模拟实验均在0.1 K下进行.综上所述，针对碳纳米结构力学特性的分子动力学模拟，合适的模拟参数确定为：0.1 K的系统温度，0.5 fs的时间步长和0.01 nm/ps的加载速率.

3 结果与讨论

3.1 拉伸力学特性分析

受轴向拉伸时，等量碳原子组成的碳纳米锥和纳米管的载荷-应变关系曲线如图2所示.轴向应变定义为纳米结构轴向长度的变化量与其原长的比值的百分数.与文献[15］的分步拉伸-松弛的实验结果不同，图2表明碳纳米锥的轴向载荷随着应变的增加趋近于线性递增，未见明显非线性变化.碳纳米管的轴向载荷与应变则以非线性变化为主.对于碳纳米锥，其拉伸应变极限随着锥角的增大而增加;但其拉伸载荷极限由C4增加到C2达到最大值后，C1的载荷极限反而陡然降低.对于碳纳米管，其拉伸载荷极限与C1相当，而应变极限则介于C2和C3之间.这些纳米结构的拉伸载荷极限和应变极限数值分别列于表1.拉伸实验的系统环境温度通过Berendsen方法控制在0.1 K，以尽量减少热扰动对结构本征力学性能的影响.碳纳米锥C2受拉时的系统温度随时间的变化曲线如图3所示，嵌入图为曲线的部分放大图形.可见，在C2受拉过程中，系统温度除了在破坏阶段附近出现激烈波动以外，在其他过程基本保持恒定.因为系统的热力学温度T主要取决于系统动能Ke，即T=2/3(Ke/N/kB)，N为系统原子数，kB是Boltzmann常数.通过观察C2拉伸模拟的构形演化，系统温度的突变主要是由C—C原子键断裂引起的碳原子飞逸脱离速度的激增产生的.

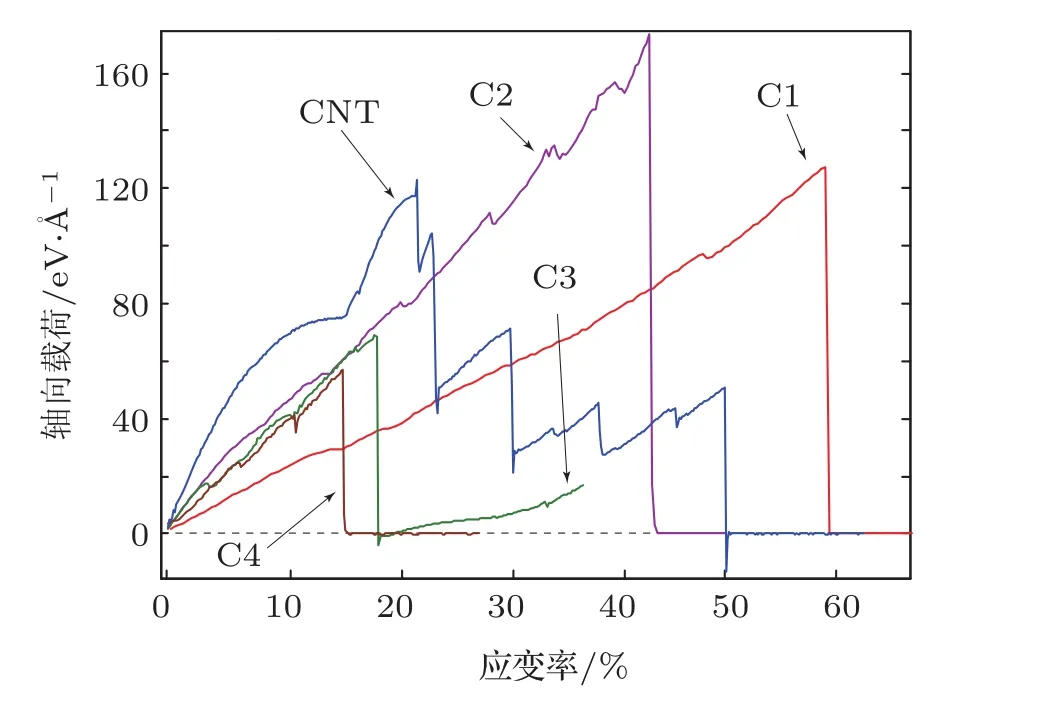
图2 拉伸轴向载荷-应变率曲线图

碳纳米锥和碳纳米管在拉伸时显现出截然不同的构形演变特点.图4(a)给出C1碳纳米锥拉伸初始时的构形和拉伸断裂之前的构形.可见，碳纳米锥出现受拉横向膨胀.然而并未如文献[15］所述，碳纳米管的拉伸应变最大而其拉伸极限载荷最小.这可能是由于碳纳米管的拉伸强度与其手性和直径有关，而本文只考虑手性为(15，0)的碳纳米管.由图2碳纳米管的载荷-应变关系曲线可以看出碳纳米管在拉伸过程中经历了弹性、屈服和强化等明显的塑性材料拉伸变形阶段.在达到其拉伸强度极限之后，碳纳米管出现了明显的阶段性颈缩变形(图2CNT曲线的阶梯状部分).最后，碳纳米管形成了藕断丝连式的单列碳原子链[23](如图4(b)所示).对于碳纳米锥，类似单列碳原子链却是只出现在C3的拉伸实验.之前的模拟结果表明，碳纳米锥C2在高温(500 K)条件下也能形成单列原子链.然而，关于通过拉伸碳纳米锥形成单列碳原子链的机理及其影响因素仍有待进一步的研究.

表1 拉伸载荷极限和拉伸应变极限

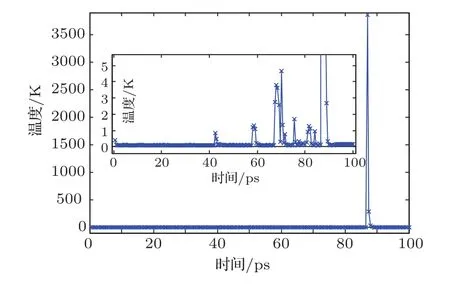
图3 C2拉伸过程的温度-时间变化曲线，嵌入图为局部放大图

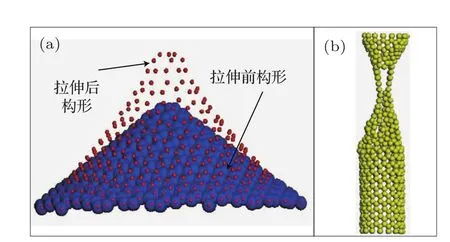
图4 拉伸构形演变特点 (a)膨胀的C1构形;(b)颈缩的CNT构形

3.2 压缩力学特性分析

等量碳原子组成的碳纳米锥和纳米管在受石墨烯刚板轴向压缩时的载荷-应变关系曲线如图5所示.压缩应变定义为石墨烯刚板和纳米结构固定端之间距离的变化量与纳米结构原长的比值的百分数.总体而言，碳纳米锥的受压载荷极限和应变极限均随着锥角的增加而增大.然而，锥角最大的C1受压载荷极限却最小.对于C1，C2，C3和碳纳米管，受压载荷极限定义为图5曲线中载荷的最大值;对于C4，受压载荷极限则取其载荷-应变曲线的第一个峰值(点1).表2列出了各纳米结构的受压载荷极限和应变极限数值.显然，碳纳米管在这些纳米结构中的受压力学特性既不突出也不逊色.

表2 压缩载荷极限和应变极限

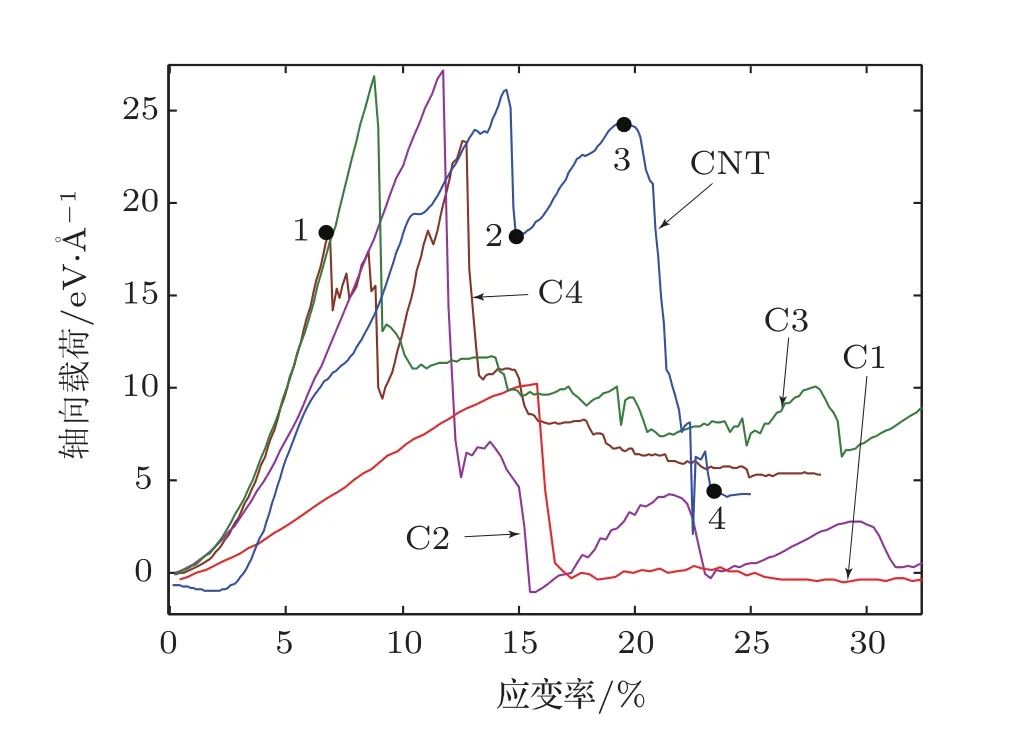
图5 压缩轴向载荷-应变率曲线图

观察其构形演化过程，碳纳米锥的受压载荷极限均出现在其屈曲的临界状态.然而，碳纳米管所受载荷还没达到最大值之前，其结构已先后出现末端原子外扩和径向屈曲，如图6(a)和图6(b)所示.在经受最大压载之后，碳纳米管承载能力随之下降.此时碳纳米管正在另一区域逐步形成新的径向屈曲结构，如图6(c)所示.待到新结构稳定之后，碳纳米管的承载能力有所恢复(见图5曲线上点2至3段).随着压缩的继续，两个径向屈曲结构通过碳纳米管的扭转变形逐渐融合成稳定的侧向屈曲变形结构，如图6(d)所示.在这过程中碳纳米管的承载能力迅速减弱至图5曲线上点4位置.注意到图5的C4载荷-应变曲线存在两个峰值，通过观看C4受拉时构形的演化过程发现，第一个峰值对应C4顶端2个碳原子受压侧向滑移的临界状态(图7(a))，而第二个峰值则是C4发生明显侧向失稳(图7(b))的临界载荷.虽然C3受压也是发生侧向屈曲，但由于其顶端原子侧移并不明显且几乎与侧向屈曲同时发生，因此其载荷-应变曲线只出现一个峰值.此外，C2和C1受压屈曲变形均为顶端原子沿轴向向内塌陷并逐渐扩大，进而最终发生类似“翻口袋”的完美手性翻转[13]，如图8(a)和8(b)所示.

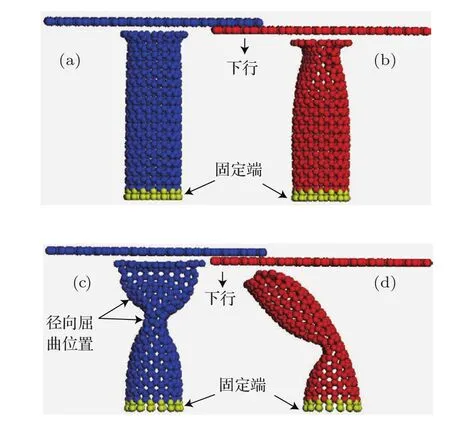
图6 CNT阶段受压的构形图 (a)顶端原子外扩;(b)首个径向屈曲;(c)双向径向屈曲;(d)侧向屈曲

图7 C4的受压构形图 (a)顶端原子侧向滑移;(b)侧向屈曲

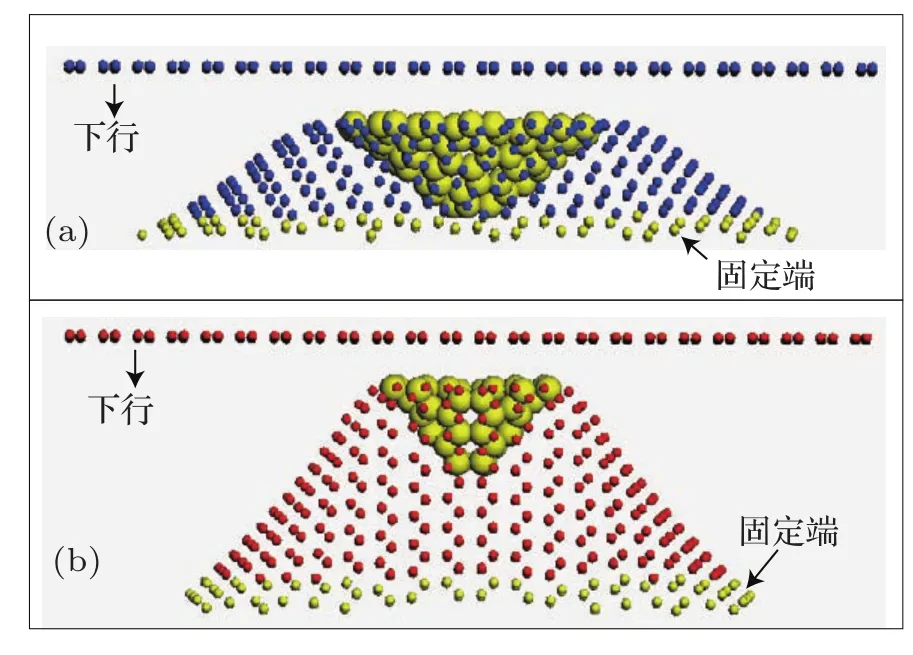
图8 碳纳米锥受压顶端内陷构形图 (a)C1;(b)C2

4 结论

本文通过分子动力学方法模拟对等量碳原子组成的碳纳米锥的拉伸和压缩实验，获得其受拉/压载荷-应变关系曲线、载荷极限和应变极限、构形演化等特性，并与碳纳米管进行对比研究.研究结果表明：1)碳纳米锥的受拉/压载荷极限随着锥角的增大先增大后减小，而其受拉/压应变极限均随着锥角的增大而增大，其中，83.62°锥角的碳纳米锥的受拉/压载荷极限最大，而112.88°锥角的C1受拉/压应变极限最大，这些碳纳米锥的力学特性毫不逊色于等量原子组成的碳纳米管;2)在受拉过程中，与碳纳米管不同的是碳纳米锥并没有呈现出明显的屈服和强化阶段特点，且其受拉载荷-应变曲线在断裂之前近似于线性变化;3)在受压过程中，与碳纳米管呈现出丰富的径向屈曲/扭转/侧向屈曲组合变形不同，碳纳米锥呈现出较为单一的轴向手性反转(83.62°和112.88°锥角的C2和C1)或侧向屈曲(38.94°和60°锥角的C4和C3).本文的研究结果表明，碳纳米锥的力学特性可媲美碳纳米管而应用于广泛的纳米科技工程领域，例如纳米传感器或纳米复合材料.

[1］Iijima S 1991Nature354 56

[2］Mahar B，Laslau C，Yip R，Sun Y 2007Sens.J.IEEE.7 266

[3］Hill E W，Vijayaragahvan V，Novoselov K 2011Sens.J.IEEE.11 3161[4］Adisa O O，Cox B J，Hill J M 2011J.Phys.Chem.C 115 24528

[5］Allen M J，Tung V C，Kaner R B 2010Chem.Rev.110 132

[6］Ge M，Sattler K 1994Chem.Phys.Lett.220 192

[7］Krishnan A，Dujardin E，Treacy M M J，Hugdahl J，Lynum S，Ebbesen T W 1997Nature388 451

[8］Iijima S，Yudasaka M，Yamada R，Bandow S，Suenaga K，Kokai F，Takahashi K 1999Chem.Phys.Lett.309 165

[9］Yang N，Zhang G，Li B 2008Appl.Phys.Lett.93 243111

[10］Lu X，Yang Q，Xiao C，Hirose A 2006Appl.Phys.A：Mate.Sci.Proc.82 293

[11］Zhang S，Yao Z，Zhao S，Zhang E 2006Appl.Phys.Lett.89 131923

[12］Wei C Y，Srivastava D 2004Appl.Phys.Lett.85 2208

[13］Jordan S P，Crespi V H 2004Phys.Rev.Lett.93 255504

[14］Tsai P C，Fang T H 2007Nanotechnology18 105702

[15］Wei J X，Liew K M，He X Q 2007Appl.Phys.Lett.91 261906

[16］Liew K M，Wei J X，He X Q 2007Phys.Rev.B 75 195435

[17］Firouz-Abadi R D，Amini H，Hosseinian A R 2012Appl.Phys.Lett.100 173108

[18］Shen H J，Shi Y J 2007J.Atom.Mole.Phys.24 883(in Chinese)[沈海军，史海进2007原子与分子物理学报24 883］

[19］Plimpton S 1995J.Comp.Phys.117 1

[20］Brenner D W 1990Phys.Rev.B 42 9458

[21］Brenner D W，Shenderova O A，Harrison J A，Stuart S J，Ni B，Sinnott S B 2002J.Phys.：Cond.Matt.14 783

[22］Liew K M，Wong C H，He X Q，Tan M J 2005Phys.Rev.B 71 075424[23］Fu C X，Chen Y F，Jiao J W 2008Sci.ChinaE：Tech.Sci.38 411(in Chinese)[付称心，陈云飞，焦继伟2008中国科学E辑：技术科学38 411］