铯Rydberg原子Stark态的避免交叉*

王丽梅 张好 李昌勇 赵建明 贾锁堂

(量子光学与光量子器件国家重点实验室，山西大学激光光谱实验室，太原 030006)

(2012年6月12日收到;2012年8月9日收到修改稿)

1 引言

Rydberg原子是外层电子被激发到主量子数很大(n≫1)的激发态原子，具有相互作用强(n4)，辐射寿命长(n3)，极化率大(n7)等奇特性质[1]因而一直受到人们的广泛关注.借助于激光冷却技术，人们可制备超冷Rydberg原子.在实验的时间尺度内，与原子间距相比，原子移动的距离可以被忽略，超冷Rydberg原子被认为是冷冻的Rydberg气体(frozen Rydberg gas)，从而可以更好地观测Rydberg原子之间的强相互作用产生的效应，成为近年来研究的热点.特别是超冷Rydberg原子系统中，两个相邻Rydberg原子之间由于强偶极-偶极相互作用产生的偶极阻塞效应[2-7]，使Rydberg原子成为实现可控量子逻辑门和量子信息处理潜在的备选介质[8].

Rydberg原子具有较大的极化率，极易受到外加电场的影响.而碱金属原子由于其离子实被Rydberg电子极化和贯穿，导致在外加电场中低-l态能级与多重态能级产生耦合，从而产生能级的避免交叉现象.1986年，Stoneman小组利用300 K的黑体辐射研究了钾原子Rydberg态的避免交叉谱[9].1995年，Gallagher小组观测到Cs原子(n+4)S态和主量子数为n(20＜n＜24)的Stark能级中最低的三个能级之间的避免交叉现象[10].2009年，美国Shaffer小组观测到束缚在核间距约为3—9µm的冷Cs Rydberg大分子[11]，该束缚态分子是利用Rydberg原子能级由外加电场导致的避免交叉所产生的势阱而形成，通过调节外加电场可以控制Rydberg-原子分子之间的相互作用.

2 实验装置

文献[12，13］已经详细地描述了该实验装置.现简述如下：将Cs原子俘获在一个标准的MOT中，背景压强约为1×10-8Pa.通过激光冷却技术，约107个Cs原子被冷却到约100µK，其高斯半径约为300µm，最大原子密度为1011cm-3.双光子激发超冷Cs原子到Rydberg态，第一步激发由冷却光提供，产生6S1/2(F=4)→6P3/2(F′=5)的跃迁，冷却光由波长调谐范围可覆盖Cs原子D2线的光栅反馈半导体激光器(Toptica，DL100)提供，输出波长为852 nm，线宽小于1 MHz.第二步激发实现6P3/2→nS的跃迁，由一台连续倍频绿光激光器(Toptica，TASHG110)提供.它由一个外腔半导体激光器输出光经放大到最大功率为1 W，然后倍频输出510 nm的激光，线宽小于2 MHz，连续可调谐范围30 GHz.整个时序的重复率为10 Hz，由信号延迟发生器(DG645)控制其时序，如图1所示.

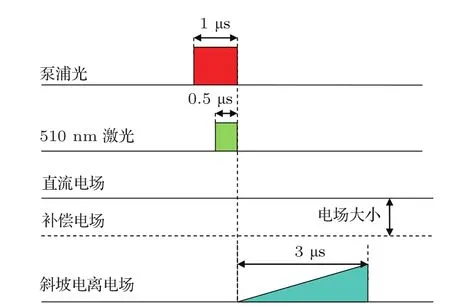
图1 时序控制图

MOT中心有两个相距15 mm的栅极.当激发光脉冲关断后，在其中一个栅极上施加高压斜坡电场电离初始产生的nS态Rydberg原子.另一个栅极上加弱的直流电场用于补偿MOT中的残余电场，同时施加直流电场研究Rydberg原子的Stark效应.场电离离子信号由微通道板(MCP)探测，通过门积分平均器(Boxcar)对信号进行取样平均，得到的平均信号进入计算机由数据采集卡(PCI-1714，Advantech)记录.实验中通过调节第二步激发光主激光器的光栅来改变510 nm激光的频率，激发不同主量子数的Rydberg原子.输出激光的波长由波长计(High Finese-Angstrom，WSU-30)进行测量.

3 实验结果和分析

我们将第二步激发光的频率调谐到6P→47S的跃迁附近，扫描激发光频率，测量不同外加电场下的离子谱.图2(a)是基于能量矩阵对角化的理论[14]计算出的CsRydberg原子47S附近的Stark能级图，图2(b)所示为测量的Rydberg原子数与电场的依赖关系，从图中可见，随着电场的变化，测量的原子数会在某几个电场处突然减少.与图2(a)的Stark谱相比，发现原子数突然减少的电场与Stark谱中的避免交叉点相对应(如图中三条竖直虚线所示).由此可推断，该现象是由于在避免交叉点处不存在与激发光共振的能级导致原子的激发几率减小的缘故.实验测得的避免交叉点和理论计算的Stark能谱的避免交叉点所对应的电场基本符合，但计算的避免交叉点对应的电场值与测量结果有一些微小的差别，其原因可能是：1)理论计算的是一个Cs Rydberg原子在电场下的Stark效应，而实验中所激发的Rydberg原子数是原子系综的结果;2)实验中补偿电场的测量所引起的误差，实验中所加的补偿电场只能补偿水平方向的电场，竖直方向的电场由于MOT中栅极的限制没有补偿，因此MOT中存在的竖直方向的杂散电场可能会对测量结果产生影响.

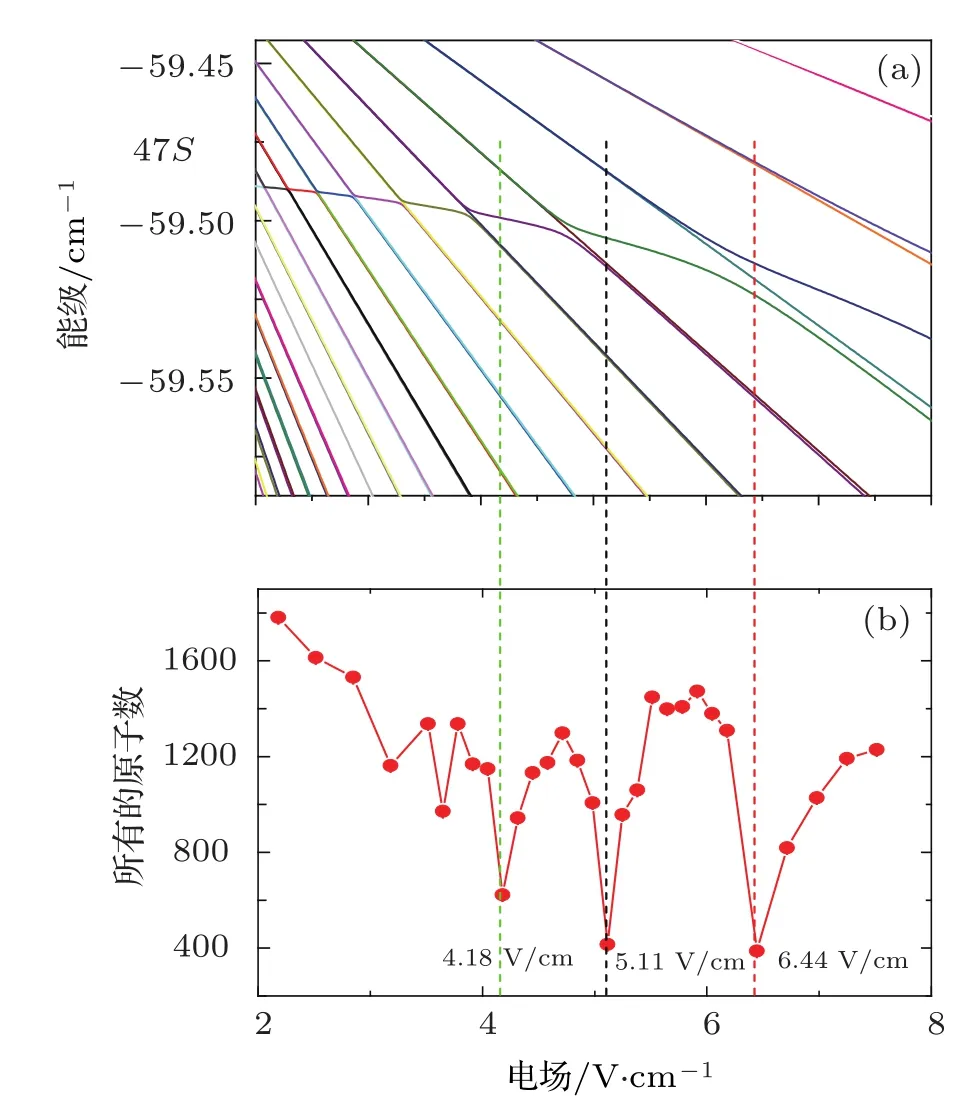
图2 (a)理论计算的外电场中47S和n=43多重态能级附近的Stark谱;(b)实验测得的47S总原子数随着电场的变化情况.三条竖直的虚线表明在4.18，5.11和6.44 V/cm处测得的原子信号的减小，分别对应Stark谱的三个避免交叉点

为了进一步研究Stark态避免交叉点的特性，将原子激发到49S态，详细研究外加电场为6.0V/cm附近的避免交叉现象，结果如图3所示.图3(a)中给出理论计算的Cs Stark谱中49S与主量子数为45的高-l态能级的避免交叉;图3(b)和(c)分别为外加电场是5.38和6.11 V/cm时测得的相应于图3(a)中A(A′)和B(B′)两个Stark态的离子谱.可以看出，测量的两个离子谱中各自的两个信号峰的中心频率差基本与理论计算结果相符合(如图中4条水平虚线所示).从离子信号的相对强度粗略来看，随着电场的变化，A和B能级的原子布居数发生相应的变化.

为了更加详细地研究避免交叉处A与B Stark态的变化过程，我们测量了更多电场下A和B两能级对应的离子谱，得到能级间隔(图4(a))以及总的原子数(图4(b))随电场的变化关系.从图中可以看出：A和B两能级对应的信号中心频率差即能级间隔Δxc在实验所测的电场范围内出现先减小后增大的趋势，其中对应的最小Δxc为240 MHz，Δxc反映了电场引起原子能级间耦合强度的大小.同时对应A Stark态测得的原子总数增大，B Stark态测得的原子总数减小的趋势，证明了由于电场的作用导致nS态能级与(n-4)多重态能级形成了避免交叉点，以及经过避免交叉点时两态的变化过程.

图3 (a)49S在电场为5.38 V/cm附近的避免交叉;(b)和(c)分别对应电场为5.38和6.11 V/cm处的离子谱信号.测得的离子谱峰值频率间隔与理论计算基本符合(如水平虚线所示)

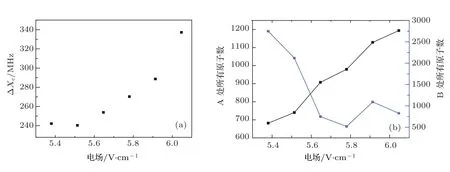
图4 49S Rydberg态在电场中回避交叉处相应于图3(a)中A和B Stark态中心频率差Δxc(a)，原子数(b)与电场的依赖关系

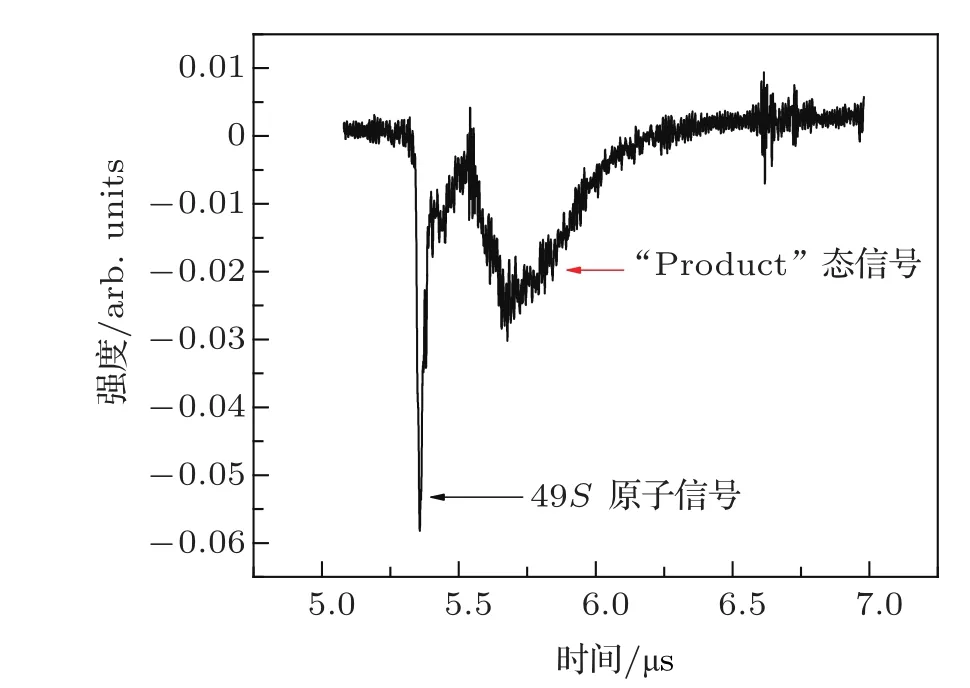
图5 49S Rydberg态在电场强度为5.38 V/cm时的TOF信号，第一个主峰为49S态的信号，第二个峰为由于电场的作用产生的 “Product”态的信号

实验中，我们发现在电场的作用下初始激发的nS态原子经避免交叉可跃迁到高-l态.图5所示为初始激发到49SRydberg态在电场强度为5.38V/cm时的时间飞行(TOF)信号.在主信号49S的旁边产生了一个“Product”态，实验测量的“Product”态的电离阈值远大于49S态的电离阈值.研究发现，它的产生依赖于外加电场的大小，并且只有当外加电场大于49S与n=45的多重态第一避免交叉点对应的电场时才能观察到“Product”的态产生.由此说明“Product”态的产生与Rydberg原子的Stark效应以及由此产生的避免交叉现象有关，我们将另文详细研究这种现象.我们可以利用这种新的实验方法克服禁界跃迁的限制来制备高-l态的原子，同时我们也可以研究态转移制备的高-l态原子之间的相互作用以及它们在电场中的可控性.

4 结论

本文主要观测了超冷Cs Rydberg原子49S态在电场为6.0 V/cm附近离子谱的变化特征，通过与理论计算的Stark谱对比，分析了外电场作用下的nS态原子与主量子数为(n-4)高-l态相互作用导致的避免交叉现象.并在实验中观察到由避免交叉产生的态转移现象，这种现象提供了一种制备高-l态的方法，为制备和研究高-l态原子之间的相互作用提供了新的实验手段.另一方面，在外电场产生的避免交叉点附近可以形成束缚势阱而形成巨型Rydberg分子[11]，所以本文的研究为进一步研究形成超冷巨型Rydberg分子具有重要的意义.

[1］Gallagher T F 1994Rydberg Atoms(Cambridge：Cambridge University Press)p25

其四，思想解放、学术规范与学术净化氛围日益浓厚。改革开放带来的观念解放几乎推倒所有人造之“神”，也几乎冲破所有人文社会科学研究的禁区。外在精神氛围自由开放、“百无禁忌”的同时，内在学术研究的严谨规范、“自说自话”遂日益成为学界的自觉追求，这也是人文社会科学作为一种现代学术必须真正摆脱其早期的自发随意性和任意蹈袭印记，而显现其科学独创品格的本质要求所在。人文社科领域近年出现的不少学术批评，爆发的多起学术“打假”事件，都属学界内部的这种激浊扬清，归根到底都属学术研究的一种自我净化；这种激浊扬清和自我净化将各种假学术、劣学术、浅学术不断逐出学术行列，从而日益厚化扎实严谨的学风和健康清新的文风。

[2］Ga¨etan A，Miroshnychenko Y，Wilk T，Chotia A，Viteau M，Comparat D，Pillet P，Browaeys A，Grangier P 2009Nature Phys.5 115

[3］Urban E，Johnson T A，Henage T，Isenhower L，Yavuz D D，Walker T G，Saffman M 2009Nature Phys.5 110

[4］Comparat D，Pillet P 2010J.Opt.Soc.Am.B 27 A 208

[5］Tong D，Farooqi S M 2004Phys.Rev.Lett.93 063001

[6］Vogt T，Viteau M 2006Phys.Rev.Lett.97 083003

[7］Vogt T，Viteaut M 2007Phys.Rev.Lett.99 073002

[8］Jaksch D，Cirac J I，Zoller P，Rolston S L，Cˆot´e R，Lukin M D 2000Phys.Rev.Lett.85 2208

[9］Stoneman R C，Janik G，Gallagher T F 1986Phys.Rev.A 34 2952

[10］Nosbaum P，Bleton A，Cabaret L，Yu J，Gallagher T F，Pille P 1995J.Phys.B 28 1707

[11］Overstreet K R，Schwettmann A，Tallant J，Booth D，Shaffer J P 2009Nature Phys.5 581

[12］Zhang L，Feng Z，Zhao J，Li C，Jia S 2010Opt.Express18 11599

[13］Feng Z，Zhang H，Che J，Zhang L，Li C，Zhao J，Jia S 2011Phys.Rev.A 83 042711

[14］Zimmerman M L，Littman M G，Kash M M，Kleppner D 1979Phys.Rev.A 20 2251