少节点基因调控网络的控制*
2013-04-14叶纬明吕彬彬赵琛狄增如
叶纬明 吕彬彬 赵琛 狄增如
1)(北京师范大学管理学院系统科学系,北京 100875)
2)(北京有色金属研究总院稀土材料国家工程研究中心,有研稀土新材料股份有限公司,北京 100088)
(2012年7月18日收到;2012年7月31日收到修改稿)
1 引言
随着生物技术的不断发展,基因工程被不断向前推进,海量的数据为科学家探索基因的奥秘提供了有力的支持,大量生物组织的基因被成功测序.对基因调控网络(genetic regulatory network,GRN)的研究也越来越受到各个领域的关注.其中,基因调控网络的振荡问题一直是大家关注的热点之一[1-13].早在30年前,Thomas就曾提出:基因调控网络要想形成振荡,就必需至少要有一个负反馈环(环上负反馈的个数为奇数).该论断于1995年被严格证明是正确的[14,15].近年来,该领域涌现出大量的科研成果.Goh等[16]认为基因调控网络是否能够形成振荡主要取决于网络中正负反馈环之间的竞争,如果负反馈环占优,网络呈现振荡态;如果正反馈环占优,网络则会呈现稳定态.2000年,Elowitz和Leibler等[17]成功地在实验室中制造出了首个振荡的3节点生物网络.它包括3个转录抑制蛋白,每个抑制蛋白都抑制下一个基因的转录,当某种特殊蛋白质含量发生变化时,细胞能在发光状态和非发光状态之间转换,形成一个环状回路,起到有机振荡器的作用.2002年,U.Alon发现在真实的生物网络中存在一系列非常小的结构单元(被命名为“模体”),它们在网络中出现的频率很大,并且对网络的功能起着非常大的作用.至此,大家开始把目光转移到这些小的结构单元上来,希望通过对这些模体的研究来逐渐认识整个基因网络.2006年,Nochomovitz和Li[18]运用布尔代数的方法研究了所有3节点和4节点的网络,发现这种少节点的网络中有许多是可以形成振荡的.
目前我们发现的大多数基因调控网络在大部分时间里都是处于静息态的,只有当网络受到外界刺激时,它们才会被激发到振荡态,完成各种生物功能,然后再回到静息态等待下一次刺激.对于一个原本应该处于静息态的基因调控网络,如果因为某种原因跳到了振荡态上,那么它就会不断地重复某种生物过程,导致机体功能紊乱,同时它对外界的刺激也可能不再敏感,使生物体处于严重失控状态.因此对基因调控网络的控制就显得非常重要了.
目前对生物网络的控制研究主要集中在神经网络[19,20]、蛋白质相互作用网络,对基因调控网络方面的控制还不是很多,特别是如何将一个振荡的基因调控网络控制到静息态的研究还非常少[21].本文运用多相位超前驱动方法对基因调控网络的控制进行了研究.通过大量的数值模拟,发现对于参数已经确定的基因调控网络,此方法的控制效率可以达到95%以上(10节点网络),对于参数不确定的网络,此方法的控制效率也非常高.
2 基因调控网络动力学模型
这里我们运用目前广泛采用的描述基因联合调控的动力学模型[21-25].它在抑制调控和促进调控中采用“AND”门的形式.具体的动力学模型如下:

这里xi表示第i个节点的浓度,acti(repi)代表促进(抑制)转录因子的总和.动力学(1)中一共有5个系统参量.µ表示在没有促进作用和抑制作用时的漏转录率;K是网络中促进子(抑制子)调控时的半高浓度;h是希尔系数;γ代表衰减率;表示第j个节点对第i个节点促进(抑制)作用的权重.
动力学(1)是一种强抑制模型[26],对所有的抑制调控采用“AND”门的形式[25],而对所有的促进调控采用“OR”门的形式.为了使系统具有一般性,我们让网络中所有节点的参数相同.(µi=µ=0,γi=0.1,hi=2,Ki=0.3,αi=βi=1,i=1,2,···,N[27]).
3 数值模拟
3.1 主相位超前驱动方法
主相位超前驱动(dominant phase advanced driving,DPAD)思想最先是由Hu等[19,20]提出,并用于对神经网络的控制中.其主体思想是:对于一个随机的网络,网络当中每一个节点都是不能自发产生 振荡的,它们如果想形成振荡就必须受到别的节点的驱动,当然这里的驱动可以来自一个节点也可以来自多个节点,但必需至少要有一个来自外界的驱动.可以通过一系列的定义找到网络中每个节点的驱动点(作为这个节点的上游节点).再通过一定的定义即可以从每个节点的所有上游节点中找出对其影响最大的节点,该节点的驱动即为主超前相位驱动(其他上游节点的驱动此时可以去掉).这样网络中的每个节点都将有且只有一个主超前相位驱动,即每个节点都只剩下一个上游节点,这样整个网络必定会变成一个一维环状结构.运用这种方法找到的环状结构对于神经网络的调控具有非常重要的意义.而将这种方法应用到基因调控网络中,找到的环状结构也意义非凡[21].如图1所示,图1(a)为一个10节点的随机振荡基因调控网络,图1(b)为运用主相位超前驱动方法找到的环状结构.从这种环状结构中不仅可以清楚地找到振荡基因调控网络的振荡源,还可以看到网络信号在网络中的传播路径,同时还能粗略地看出网络中重要的和不重要的节点(分别用红色和白色表示),有利于对网络进行调控.
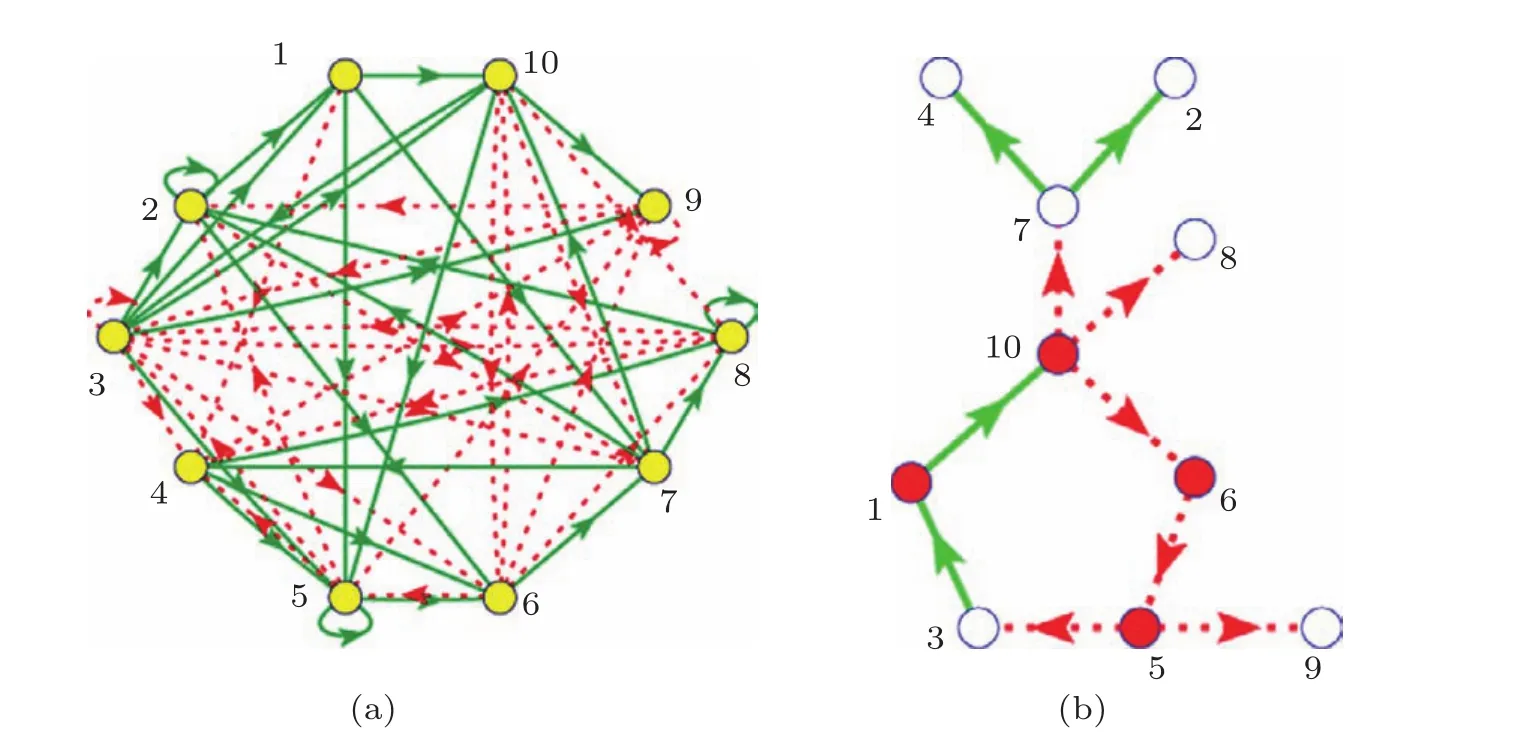
图1 少节点基因调控网络 (a)10节点随机振荡基因调控网络,其中绿色实线表示促进作用,红色虚线表示抑制作用;(b)运用主相位超前驱动方法找到的一维环状结构,其中重要节点用红色表示,不重要的节点用白色表示
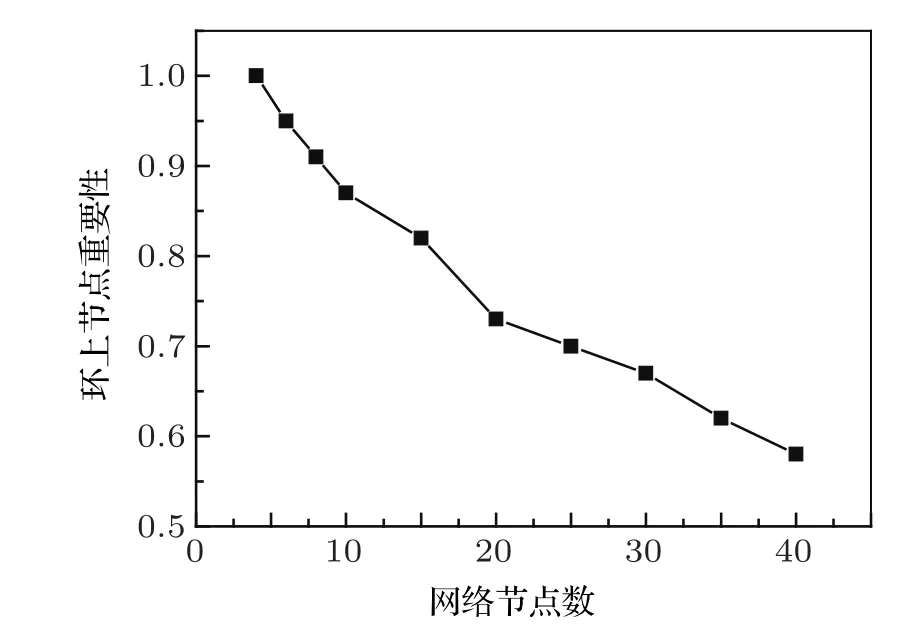
图2 不同节点数的基因调控网络,主相位超前驱动环上的节点重要性
这里,网络中重要的节点指的是去掉这个节点网络就会从振荡态到达稳定态;不重要的节点指的是去掉这个节点,网络的振荡态不会发生改变.运用主相位超前驱动方法对原始网络进行简化,可以得到:对于少节点的网络,重要的节点几乎都在环上,不重要的节点几乎都在环外.但是随着网络节点数的增多,主相位超前驱动方法在区分节点的重要性上就会弱化.环上的节点不再重要的概率会逐渐增高.如图2所示,经过大量的数值模拟可以看出,当网络节点数少于10个时,环上的节点是重要节点的概率超过了90%;而当网络上的节点多于10个时,环上节点是重要节点的概率近似以线性比例下降;当网络节点数达到40个时,环上节点为重要节点的概率下降到只有57.9%.
3.2 多相位超前驱动方法
我们对主相位超前驱动方法做了适当的修改,将之变为多相位超前驱动方法.运用这种方法可以将找到重要节点的概率大大提高.具体的做法如下:1)给网络中每个节点定义一个相位[21];2)找出每个节点的上游节点(将上游节点指向下游节点的连边定义为重要连边);3)简化原始网络,将网络中的重要连边留下,组成相位超前驱动网络;4)找出相位超前驱动网络中所有的负反馈环;5)统计相位超前驱动网络中每个节点参与的负反馈环数并排序.如图3所示,图3(a)为图1(a)的相位超前驱动网络,图3(b)为其相位超前驱动网络中所有的负反馈环(共11个).各个节点的数据统计见表1.从表1可以看出:在相位超前驱动网络中,10号节点参与的负反馈环数最多,它是一个重要节点,控制住它,就可以控制整个网络.同时还可以看出节点参与负反馈环数排名中的前6位都是重要节点.而后4位都是不重要的节点.可见这一方法对于判断节点的重要性具有很好的效果.
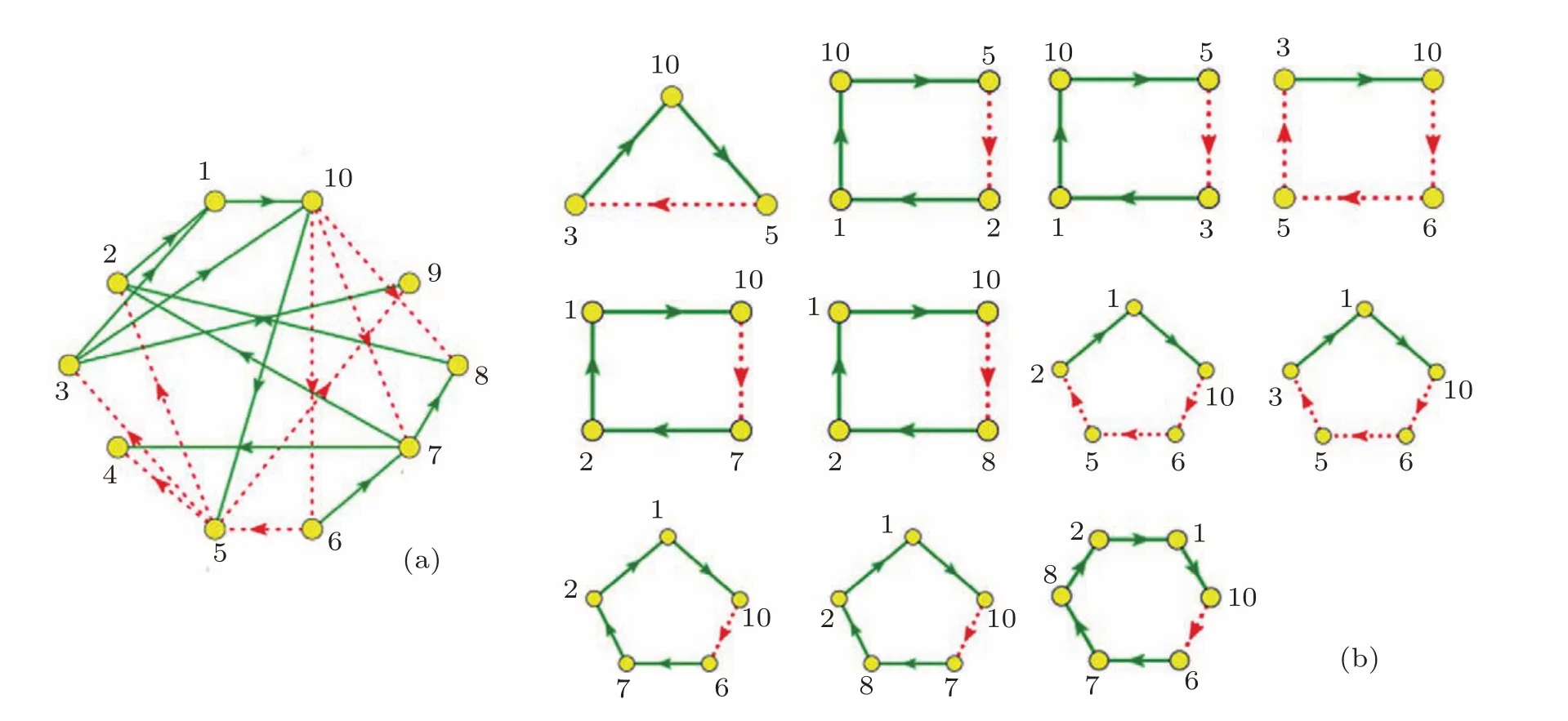
图3 相位超前驱动网络 (a)图1(a)的相位超前驱动网络;(b)(a)图中所有的负反馈环
数值模拟结果表明:随机选取10000个振荡网络,运用多相位超前驱动方法对节点参与负反馈环的排序,排在第一位的节点(以下称为“首要节点”)是重要节点的概率比用主相位超前驱动方法寻找重要节点的概率要高很多.如图4所示,可以看出运用多相位超前驱动方法找到的首要节点是重要点的概率并没有随着网络节点数的增加而大幅度下降.当网络节点数达到40个节点时,首要节点为重要节点的概率依然可以达到90%.
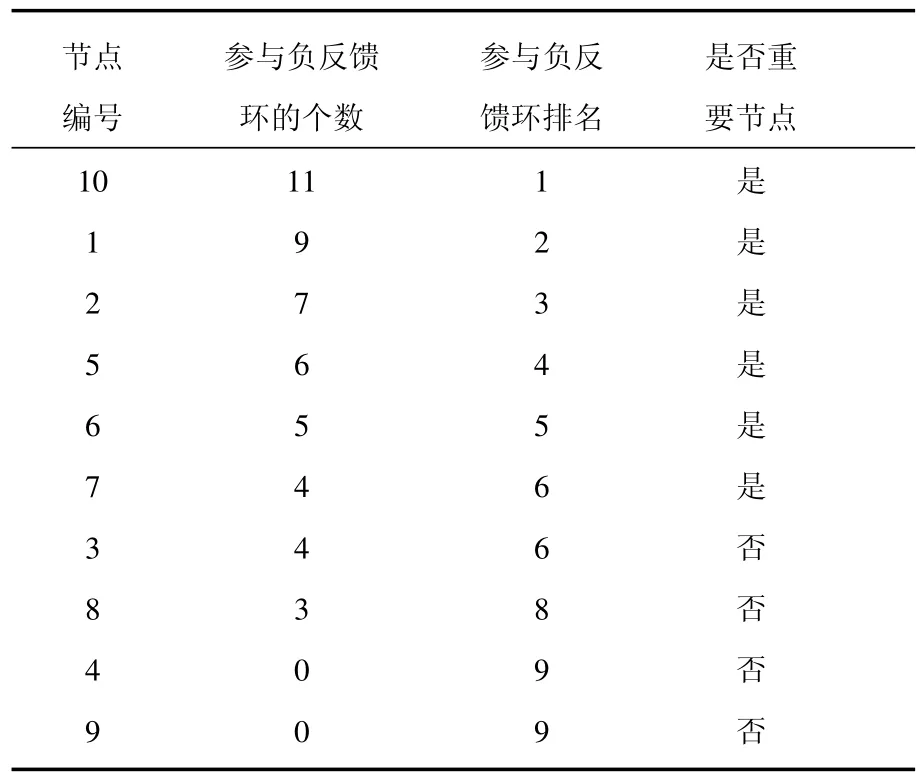
表1 多相位超前驱动法判断节点的重要性(参数确定)

图4 不同节点数的基因调控网络,运用多相位超前驱动方法找到的首要节点为重要节点的概率
以上是在系统参数确定的情况下,运用多相位超前驱动方法寻找网络重要节点的结果.那么当系统的参数不确定时,如何来寻找网络的重要节点呢?数值模拟表明运用多相位超前驱动方法依然可以有效地找到网络中的重要节点.具体方法是:将系统参数在其各自有效的范围内[27]划分为若干个点,然后在每个参数点上统计出各个节点在相位超前驱动网络上参与的负反馈环的个数,最后统计在所有参数点上各个节点在相位超前驱动网络上参与的负反馈环的总个数,并依此排序.
还是以图1(a)所示的网络为例.通过数值模拟,我们发现:运用多相位超前驱动方法找到的在所有参数点上的相位超前驱动网络中参与负反馈环最多的节点(10号节点,以下称为“头号节点”),其平均重要性达到了100%(这里的平均重要性指的是:对所有的参数点[27],控制目标节点后,网络能够被有效控制到稳定态的平均概率),其他节点的平均重要性见表2.从表2可以看出:网络节点的平均重要性与其参与的负反馈环的总排名关系很大.

表2 多相位超前驱动法判断节点的重要性(参数不确定)
我们用数值模拟的方法对10000个10节点的网络进行了统计,结果表明:在系统参数不确定的情况下,运用多相位超前驱动方法找到的头号节点,其平均重要性为100%的概率为92%.对于其他节点数的网络,我们也做了类似的统计,结果如图5所示.

图5 不同节点数的基因调控网络,头号节点平均重要性为100%的概率
我们认为多相位超前驱动方法之所以比主相位超前驱动方法能更好地寻找到网络当中的重要点,是因为在主相位超前驱动中只保留了对被驱动节点贡献最大的上游节点,而忽视了其他上游节点的作用.这样就导致了网络简化过程中只保留下来惟一一个负反馈环,并被认为是网络振荡的源.从数值统计上看,这惟一一个负反馈环上的节点是重要节点的概率比环外的节点要高很多.但这其中还是有节点是不重要的,它们出现在环上也许只是因为其所控制的下游节点只有它这一个上游节点,或者有多个上游节点但是每个上游节点的贡献都很小.而运用多相位超前驱动方法就可以很好地避免上面的问题.在多相位超前驱动中,我们将原始网络中所有的重要连边都保留下来,形成相位超前驱动网络,该网络是对原始网络的简化,同时又保留着原始网络中的重要信息.根据Goh等[16]的理论,以及我们之前的一些研究结果表明:负反馈环对于网络的振荡起着促进作用(当然这其中各种负反馈环所起的作用大小不同,但是定性上来说还是促进的[28]),那么简化后的网络中,每个负反馈环上的节点应该都对网络的振荡起着一定的作用.如果把这些作用累加起来,就可以看作是该节点对网络振荡所起的总贡献,这样总贡献的排序即可以在一定程度上反映网络中节点的重要性.
4 结论
基因调控网络是目前大家研究的一个热点,而它的自组织振荡又是其中的核心问题.如何来控制自组织振荡是问题的关键.主相位超前驱动方法对于少节点的网络可以较好地找到网络中的重要节点,但是对于节点数较多的网络,这种方法找到重要节点的概率会呈线性下降.运用多相位超前驱动方法则可以很好地解决上述问题.对于系统参数已经给定的网络,运用该方法找到重要节点的成功率明显提高.对于系统参数不确定的网络,运用该方法也可以高效率地找到网络中的重要节点.
[1]Tavazoie S,Hughes J D,Campbell M J,Cho G M 1999Nat.Genet.22 281
[2]Xu P X,Zhang X,Heaney S,Yoon A,Michelson A M,Maas R L 1999Development126 383
[3]Peterson K J,Davidson E H 2000P.Natl.Acad.Sci.USA97 4430
[4] Lee T I,Rinaldi N J,Robert F,Odom D T 2002Science298 799
[5]Ihmels J,Friedlander G,Bergmann S,Sarig O 2002Nat.Genet.31 370
[6]Ma H W,Kumar B,Ditges U,Gunzer F 2004Nucleic Acids Res.32 6643
[7]Posfai G,Plunkett G 2006Science312 1044
[8]Gilchrist M,Thorsson V,Li B,Rust A G 2006Nature441 173
[9]Kurland C G,Collins L J,Penny D 2006Science312 1011
[10]Mcadams H H,Srinivasan B,Arkin A P 2004Nature Rev.Genet.5 1
[11]Shen-Orr S S,Milo R,Mangan S,Alon U 2002Nat.Genet.31 64
[12]Lipshtat A,Purushothaman S P,Lyengar R,Maayan A 2008Biophysical Journal94 2566
[13]Kim J R,Yoon Y,Cho K H 2008Biophysical Journal94 359
[14]Snoussi E H 1998J.Biol.Sys.6 3
[15]Plahte E H,Mestl T,Omholt W S 1995J.Biol.Sys.3 409
[16]Goh K G,Kahng B,Cho K H 2008Biophysical Journal94 4270
卓别林有一句很幽默的名言:“人们为我欢呼,是因为他们对我了如指掌;人们为爱因斯坦欢呼,是因为没人弄得懂他。”的确,电影不同于高深的物理理论,卓别林用最直接的方式向不同层次的观众们传达着自己想要表达的观点,这是人们喜欢他的原因。
[17]Elowitz M B,Leibler S 2000Nature403 335
[18]Nochomovitz Y D,Li H 2006P.Natl.Acad.Sci.USA103 4180
[19]Qian Y,Liao X,Huang X,Hu G 2010Phys.Rev.E 81 036101
[20]Liao X,Hu G 2011Front.Phys.6 124
[21]Ye W,Huang X,Li P,Hu G 2010Phys.Lett.A 374 2521
[22]Li C,Chen L,Aihara L S,Kazuyuki L 2006IEEE53 2451
[23]Mangan S,Alon U 2001P.Natl.Acad.Sci.USA100 11980
[24]Setty Y,Mayo A E,Surette M G,Alon U 2003P.Natl.Acad.Sci.USA100 7702
[25]Ishilara S,Fujimoto K,Shibata T 2005Genes to Cells10 1025
[26]Wu Y,Zhang X,Yu J,Ouyang Q 2009PLoS Computational Biology5 e1000442
[27]Ye W,Li P,Huang X,Hu G 2010Phys.Lett.A 374 4749
[28]Ye W,Zhang Z,L¨u B,Di Z,Hu G 2012Chin.Phys.B 21 060203
