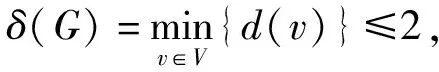通有构形的特征多项式
2020-02-10高瑞梅
孙 莹, 高瑞梅
(长春理工大学 理学院, 长春 130022)
0 引 言
设K是一个域,V是域K上的n维向量空间, 将V中有限个超平面所组成的集合称为一个超平面构形, 简称构形, 记为A.若构形A所在空间V的维数为n, 则定义A的维数为n.
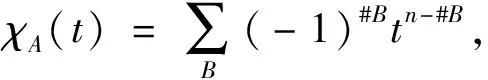
设W是欧氏空间E=n中的一个有限Weyl群, 固定W的一个正根系Φ+.对于任意α∈Φ+,k∈, 定义超平面H(α,k)={v∈E|α(v)=k}, 则构形A={H(α,0)|α∈Φ+}就是与W对应的Weyl构形.Weyl构形的变形形式有Shi构形、 Catalan构形和Shi-Catalan构形等, 目前已成为该领域的研究热点[3-8].An-1型Weyl构形, 也称为braid构形, 包含个超平面:xi-xj=0, 1≤i xi-xj=aij, 1≤i (1) 其中aij是通有元素.式(1)为一个特殊的通有构形, 称为通有braid构形.文献[2]借助图论中的森林给出了其特征多项式的计算方法. 本文首先推广平凡位置构形, 给出广义平凡位置构形的定义, 并确定平凡位置构形、 广义平凡位置构形、 通有构形之间的关系.结果表明:平凡位置构形、 广义平凡位置构形、 通有构形构成的3个集合, 前者是后者的真子集.其次, 利用通有构形的特征多项式推导出广义平凡位置构形的特征多项式.最后, 研究阈构形xi+xj=0(1≤i xi+xj=aij, 1≤i 其中aij是通有元素, 称为通有阈构形.利用文献[9-11]的方法, 通过建立线性无关子构形与不包含偶圈简单图之间的关系, 给出通有阈构形子构形的特征多项式. 定义1[2]设A是一个n维构形, 对于H1,…,Hp∈A, 如果满足: 1)当p≤n时, dim(H1∩…∩Hp)=n-p; 2)当p>n时,H1∩…∩Hp=Ø. 则称A处于平凡位置或A是一个平凡位置构形. 定义2设A是一个n维构形,A可表示为一些子构形的不交并:A=B1∪…∪Bm, 且Bi含有ki个超平面,ki≥1, 1≤i≤m.如果A满足以下条件: 1)Bi中任意两个超平面均平行, 即超平面的法向量平行, 1≤i≤m; 2)对任意的Hi∈Bi(1≤i≤m),H1,…,Hm均处于平凡位置. 则称A为广义平凡位置构形. 由定义2可见, 如果k1=…=km=1, 则A是一个平凡位置构形, 即广义平凡位置构形是平凡位置构形的推广. 定义3[2]设A是一个n维构形, 定义为L1(v)=a1, …,Lm(v)=am.如果a1,…,am是通有元素(即Hi1∩…∩Hik≠Ø与Li1,…,Lik线性无关是等价的, 其中Hi=Ker(Li(v)-ai)), 则称A为通有构形. 定理1广义平凡位置构形必为通有构形. 证明:设A是一个广义平凡位置构形, 则A可表示为一些子构形的不交并:A=B1∪…∪Bm.任意选取A中的p个超平面H1,…,Hp, 如果H1∩…∩Hp=Ø, 则有下列两种情形: 1)存在Hi,Hj(1≤i 2)H1,…,Hp来自于B1,…,Bm中不同的p个构形, 则H1,…,Hp处于平凡位置, 由定义1得p>n, 因此p个n维向量L1,…,Lp线性相关. 反之, 若L1,…,Lp线性相关, 则也存在下列两种情形: 1)存在i,j(1≤i 2)H1,…,Hp来自于B1,…,Bm中不同的p个构形, 即H1,…,Hp处于平凡位置; 若p≤n, 则由定义1, dim(H1∩…∩Hp)=n-p, 即H1,…,Hp的法向量L1,…,Lp线性无关, 矛盾.因此p>n, 故H1∩…∩Hp=Ø.证毕. 由于平凡位置构形是特殊的广义平凡位置构形, 因此由定理1可得如下推论. 推论1平凡位置构形必为通有构形. 由于广义平凡位置构形是通有构形, 因此可借助通有构形的特征多项式, 计算广义平凡位置构形的特征多项式. 定理2n维广义平凡位置构形A=B1∪…∪Bm(ki=#Bi, 1≤i≤m)的特征多项式为 文献[2]利用构形的交叉偏序集与截断的Boolean代数同构方法, 得到了平凡位置构形的特征多项式.利用定理2, 令k1=…=km=1, 则易得如下推论. 推论2设A是包含m个超平面的n维平凡位置构形, 则A的特征多项式为 易见, 3个平面x=0,y=0,x+y-1=0形成的3维构形是通有构形, 但不是广义平凡位置构形.因此, 平凡位置构形、 广义平凡位置构形、 通有构形构成的3个集合, 前者是后者的真子集. 定义4[2]由超平面xi+xj=aij(1≤i 定义5设B是Tn的一个子构形, 定义B对应的简单图G=(V,E), 其中: V=[n]={1,2,…,n};E={ij|Ker(xi+xj-aij)∈B}. B中超平面xi+xj=aij的法向量为αij=εi+εj, 其中εi是第i个n维单位向量, 也称αij为G的边ij对应的向量. 定义6若构形B中超平面的法向量线性无关(相关), 则称B线性无关(相关), 也称B对应的图G线性无关(相关). 定义7[12]起点和终点重合的轨道称为圈;长度为奇数(偶数)的圈称为奇圈(偶圈). 引理2偶圈线性相关. 证明:设偶圈的顶点集为V={1,2,…,2k},k≥2, 边对应的向量依次为 α12=ε1+ε2,α23=ε2+ε3, …,α2k-1,2k=ε2k-1+ε2k,α2k,1=ε2k+ε1. 由于α12+α34+…+α2k-1,2k=ε1+…+ε2k=α23+α45+…+α2k,1, 则偶圈的边对应的向量组线性相关, 即偶圈线性相关. 引理3奇圈线性无关. 证明: 设奇圈的顶点集为V={1,2,…,2k+1},k≥1, 边对应的向量依次为 α12=ε1+ε2,α23=ε2+ε3, …,α2k,2k+1=ε2k+ε2k+1,α2k+1,1=ε2k+1+ε1. 假设l1α12+l2α23+…+l2kα2k,2k+1+l2k+1α2k+1,1=0, 即 (l1+l2k+1)ε1+(l1+l2)ε2+…+(l2k+l2k+1)ε2k+1=0. 由于ε1,…,ε2k+1线性无关, 因此l1=…=l2k+1=0, 即奇圈线性无关. 下面从图的角度给出通有阈构形的子构形线性无关的充要条件. 定理3设G=(V,E)是n个顶点的简单图, 则G线性无关当且仅当G不含偶圈, 且G的每个连通分支C均满足e(C)≤v(C), 其中e(C)和v(C)分别表示C的边数和顶点数. 证明:G的子图G1的边对应的向量无论是v(G1)维还是n维, 并不影响G1的线性相关性, 因此下面证明中不再明确指出子图的边对应向量的维数. 1)若G含偶圈, 则由引理2,G线性相关.若G的某一个连通分支C满足e(C)>v(C), 则e(C)个v(C)维向量必线性相关, 即C线性相关, 因此G线性相关.综上, 若G线性无关, 则G不含偶圈且G的每个连通分支C均满足e(C)≤v(C). 2)假设G不含偶圈且G的每个连通分支C均满足e(C)≤v(C).下面对v(G)=n进行数学归纳法. ① 当n=2时,G线性无关. ② 假设n≤m-1时结论成立, 则当n=m时, 由于G不含偶圈, 故由引理4,δ(G)≤2. 情形1)当δ(G)=0时, 若e(G)=0, 则G线性无关.若e(G)≥1, 则存在顶点k∈V=[m]={1,2,…,m}, 满足d(k)=0, 即顶点k是G的孤立点.设V1={k1,…,kp}是G的孤立点集, 1≤p≤m-2, 则G-V1的每个连通分支均是G的连通分支, 且v(G-V1)=m-p≤m-1, 因此G-V1符合归纳假设, 故G-V1线性无关.又G与G-V1具有相同的边集, 因此G也线性无关. 情形2)当δ(G)=1时, 存在顶点k∈V=[m]={1,2,…,m}, 满足d(k)=1.设与k邻接的唯一顶点为l,k和l关联的边为e, 包含点k唯一的连通分支为C.对于G-k,G的连通分支C去掉了一个顶点k和一条边e成为G-k的一个连通分支, 其余连通分支不变, 因此G-k满足归纳假设, 故G-k线性无关.由于G-k不含顶点k, 因此边e对应的向量αkl=εk+εl不能由G-k的边对应的向量线性表示.故G=(G-k)+e线性无关. 由引理1和定理3, 可得n维通有阈构形Tn子构形的特征多项式的计算公式. 例1如图1所示, 其对应的构形是6维通有阈构形T6的一个子构形B,B中超平面为: 图1 T6的子构形 x1+x2=a12,x1+x3=a13, x1+x5=a15,x1+x6=a16, x2+x3=a23,x3+x4=a34, x4+x5=a45,x5+x6=a56. e(F)的值和F的情形个数列于表1. 当e(F)=4,5,6时,F分别有1,4,8种线性相关的情形, 如图2所示, 其中每个图形下面的数字表示该图形的情形个数. 表1 e(F)的值和F的情形个数 因此B的特征多项式为 图2 线性相关的子图 综上所述, 本文首先通过推广平凡位置构形, 得到了广义平凡位置构形.其次, 讨论了通有构形和广义平凡位置构形的关系, 借助通有构形的特征多项式, 给出了广义平凡位置构形的特征多项式.最后, 研究了通有阈构形, 通过建立线性无关子构形与不包含偶圈的简单图之间的关系, 给出了通有阈构形子构形的特征多项式.1 平凡位置构形与通有构形的关系
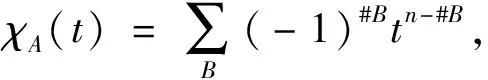

2 通有阈构形的特征多项式