极化无关双向吸收超材料吸波体的仿真与实验验证*
2013-04-14鲁磊屈绍波夏颂徐卓马华王甲富余斐
鲁磊屈绍波夏颂 徐卓 马华王甲富余斐
1)(空军工程大学理学院,西安 710051)
2)(西安交通大学,电子材料与器件教育部重点实验室,西安 710049)
(2012年6月7日收到;2012年8月5日收到修改稿)
1 引言
超材料是一类新型人工复合材料,具有许多奇异的电磁特性,如负折射率、完美透镜和隐身斗篷等[1-5].超材料另一方面的重要应用是完美吸波体[6].通过调整超材料亚波长单元的尺寸和形状,可以分别调节超材料的等效介电常数和磁导率,使得反射率R和透射率T同时达到最小,从而实现吸收率A达到最大(A=1-R-T).自2008年Landy等[6]提出微波频段完美吸收超材料吸波体后,超材料吸波体引起了研究人员的广泛关注,其研究领域也从微波频段[7-12]拓展到太赫兹[13-15]、红外[16-18]以及光频段[19-21].然而,关于双向吸收超材料吸波体却鲜有报道,这限制了其应用范围.2010年Hu等[22]提出了双向吸收平面结构超材料吸波体,但是该吸波体是极化相关的.
本文仿真设计并实验验证了一种极化无关的双向吸收平面结构超材料吸波体.通过全波仿真研究了该吸波体对不同极化电磁波在斜入射情况下的吸收效果,以及通过对单元金属结构的表面电流分布研究了其谐振特性,并分析了其损耗主要来自介质基板的介电损耗.最后,加工出实验样品并进行了测试,验证了该超材料吸波体的双向吸收特性.该吸波体吸收率高、厚度薄、设计简单且可通过按比例调节超材料吸波体的单元尺寸大小,使其工作于其他频段.
2 仿真设计和分析
超材料吸波体由三层周期金属结构组成,中间被两层介质基板隔开,如图1(a)所示.电磁波垂直入射到吸波体表面,其中电场沿+x方向,磁场沿+y方向,沿z轴的两个方向分别记为激励端口1和激励端口2.周期金属结构采用耶路撒冷十字电谐振结构,其单元形状如图1(b)所示,具体尺寸为:a=5 mm,b=4.8 mm,c=3 mm,w1=0.6 mm,w2=0.2 mm.周期金属结构由铜箔构成,其电导率为5.8×107S/m,厚度为t=0.02mm.介质基板采用FR-4双面板,其相对介电常数为εr=3.9(1+i0.03),厚度为h=0.4 mm.耶路撒冷十字结构对垂直入射电磁波具有强烈的电谐振,实现对电磁波的电耦合;而第一层与第二、三层金属结构形成环形电流,产生磁谐振,实现对电磁波的磁耦合.通过调节金属结构的尺寸和介质基板的厚度,可以调节吸波体电磁响应的频率和强度,实现吸波体与空气的阻抗匹配和高损耗.由于耶路撒冷十字结构具有四重旋转对称性,因而超材料吸波体是极化无关的.

图1 超材料吸波体结构示意图 (a)侧视图;(b)单元结构
采用基于有限元的商业电磁软件Ansoft HFSS进行全波仿真,单元金属结构周围的四个面上均设为周期边界条件.超材料吸波体仿真得到的反射率、透射率以及吸收率如图2所示.由于超材料吸波体在电磁波传播方向上是对称的,因而电磁波沿端口1和端口2入射所得到的散射参数是相同的,图2仅给出沿一个方向的结果.在10.7 GHz,反射率R=|S11|2达到最小,同时透射率T=|S21|2也非常小,此时吸收率达到最大为90.7%,半功率带宽为6.6%,从而实现双向窄带强吸收.
超材料吸波体对不同斜入射角度横电(TE)极化和横磁(TM)极化电磁波的吸收情况如图3所示.其中,θ为电磁波波矢与超材料吸波体法线的夹角.如图3(a)所示,对于TE极化波,随着斜入射角度θ的增加,吸收峰频率基本保持不变,而吸收率逐渐减小,θ为60°时,吸收率仍可达到70%.对于TM极化波,随着θ的增加,吸收峰频率发生蓝移,吸收率逐渐增大,θ为50°时,吸收率达到最大为99.3%.该超材料吸波体对斜入射TE极化和TM极化电磁波均具有较好的吸收效果.
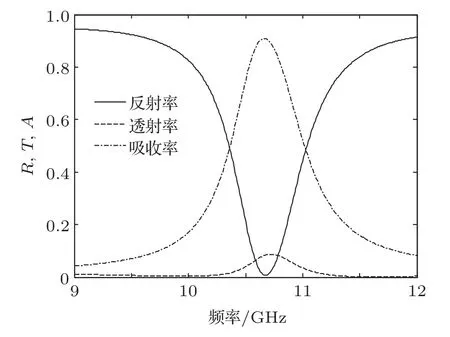
图2 超材料吸波体仿真的反射率、透射率和吸收率

图3 对不同斜入射角度下电磁波的吸收率 (a)TE极化波;(b)TM极化波
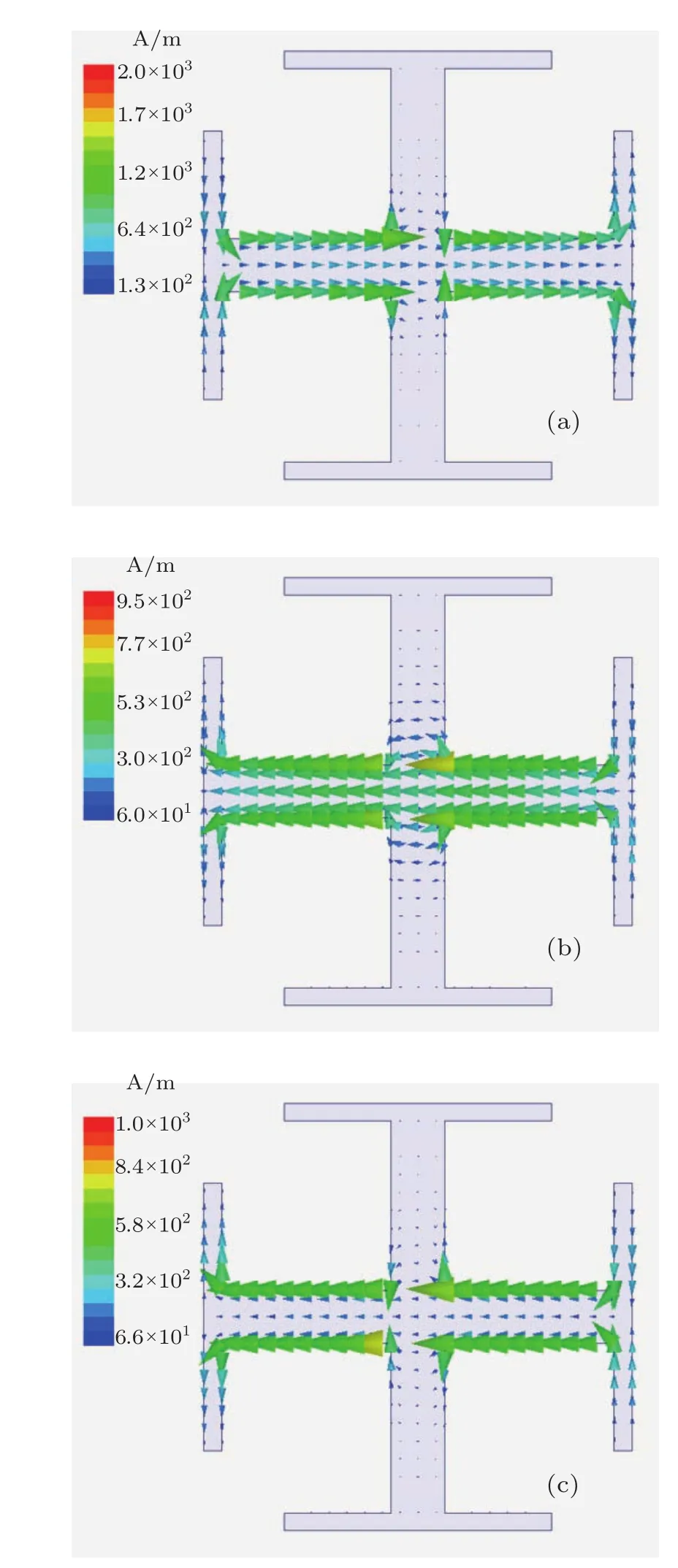
图4 吸波体单元金属结构表面电流分布 (a)第一层;(b)第二层;(c)第三层
超材料吸波体单元结构在吸收峰频率10.7 GHz的表面电流分布如图4所示.在电磁波垂直入射到超材料吸波体表面的情况下,图4(a)中第一层金属结构在平行电场的作用下产生电谐振,图4(b)和4(c)中第二层、三层金属结构上的电流方向与第一层金属结构上的电流方向相反,形成环流,产生磁谐振.在阻抗匹配时,吸波体对入射电磁波的反射最小,且超材料吸波体在谐振频率附近具有较大的金属欧姆损耗和介质基板的介电损耗,因而可以实现对电磁波的强吸收.为分析超材料吸波体的损耗来源,我们仿真了金属结构铜片或是介质基板具有损耗时的吸收率情况.如图5所示,当仅金属结构具有损耗,即铜片和无耗基板组合时,吸收率最大只有22.6%;而当仅介质基板含有损耗,即理想电导体(PEC)和损耗基板组合时,其吸收率曲线与采用金属结构铜片和损耗基板组合时的吸收率曲线基本重合,由此说明该超材料吸波体的损耗主要来自于介质基板.超材料吸波体介质基板中的单位体积能量损耗密度如图6(a)和(b)所示,介电损耗主要集中于耶路撒冷十字沿电场方向的两臂之间第一层介质基板中.

图5 超材料吸波体损耗来源分析

图6 吸波体介质基板中的单位体积能量损耗密度 (a)第一层;(b)第二层
3 实验验证
采用印刷电路板技术,首先用厚度为0.4 mm的FR-4双面板加工出前两层金属结构,再用厚度同样为0.4 mm的FR-4单面板加工出第三层金属结构,最后用粘合剂将加工出的两块样品粘在一起.最终加工出的样品实物如图7(a)所示,样品尺寸为20 mm×10 mm,共4×2个单元,每个单元金属结构的尺寸与图1(b)中的仿真尺寸相同.实验所采用的矩形波导测试系统如图7(b)所示,由HP8270ES矢量网络分析仪和X波段的BJ100标准矩形波导组成,矩形波导横截面尺寸为22.86 mm×10.16 mm,样品用泡沫固定于矩形波导的中间位置.

图7 (a)加工样品照片;(b)矩形波导测试系统

图8 实验样品测试数据 (a)S参数;(b)吸收率
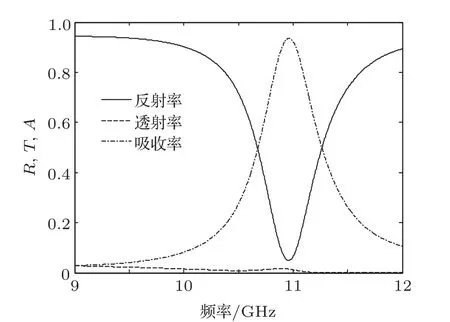
图9 仿真有限大尺寸超材料吸波体的反射率、透射率和吸收率
测试超材料吸波体样品得到的散射(S)参数如图8(a)所示,|S12|与|S21|基本重合;|S22|较|S11|差,产生很多反射,但都在11.1 GHz同时达到最小.吸收率曲线如图8(b)所示,电磁波分别沿端口1和端口2入射时,吸收率峰值依次为95.9%和90.8%.吸波体总厚度约为0.8 mm,工作波长约1/34.
图8(a)中|S22|和|S11|在高频段幅值略有不同,这主要是因为在实验样品加工制作过程中,用粘合剂将先后加工出的两块样品粘在一起,不可避免地会在样品之间引入空气层和粘合剂,导致最终加工出的样品在电磁波传播方向上不是完全对称的,即样品的两面与空气的阻抗匹配特性略有不同,从而使得反射率也略有差异;此外,实际样品在矩形波导测试系统中测试时会产生许多扰动,如图8(a)所示反射系数低谷两侧频段,这也是导致|S22|和|S11|存在差异的原因之一.
图9为仿真的与样品实物大小相同的有限大尺寸超材料吸波体在矩形波导环境下的反射率、透射率和吸收率曲线,其吸收峰频率和幅值分别为10.96 GHz和93.6%.比较图8(b)和图9中的吸收率曲线,超材料吸波体测试的吸收峰频率较仿真结果向高频移动了0.14 GHz.这主要是由于FR-4基板介电常数的不均匀性以及测试样品的有限大尺寸引起的;FR-4基板介电常数会随着频率增大而减小,而有限大尺寸会使得样品的总体电容减小,从而使得吸收峰频率向高频移动.总体来看,测试结果与仿真结果符合较好,验证了该超材料吸波体的双向吸收特性.
4 结论
本文设计制作了极化无关双向吸收超材料吸波体,该吸波体对斜入射TE极化和TM极化电磁波具有较好的吸收效果,通过金属单元结构的表面电流分布研究了其电磁谐振特性,并仿真分析了吸波体强吸收的损耗主要来自FR-4介质基板的介电损耗.加工出超材料吸波体实验样品并进行了测试,测试数据表明,该吸波体在11.1 GHz实现了双向强吸收,吸收率分别为95.9%和90.8%.该吸波体厚度较薄,工作波长约为1/34.总之,本文设计的吸波体厚度薄、设计简单,可用于雷达吸波材料,具有较好的应用前景.
[1]Veselago V G 1968Sov.Phys.Usp.10 509
[2]Smith D R,Padilla W J,Vier D C,Nemat-Nasser S C,Schultz S 2000Phys.Rev.Lett.84 4184
[3]Shelby R A,Smith D R,Schultz S 2001Science292 77
[4]Pendry J B 2000Phys.Rev.Lett.85 3966
[5]Schurig D,Mock J J,Justice B J,Cummer S A,Pendry J B,Starr A F,Smith D R 2006Science314 977
[6]Landy N I,Sajuyigbe S,Mock J J,Smith D R,Padilla W J 2008Phys.Rev.Lett.100 207402
[7]Wang B,Koschny T,Soukoulis C M 2009Phys.Rev.B 80 033108
[8]Zhang Y P,Zhao X P,Bao S,Luo C R 2010Acta Phys.Sin.59 6078(in Chinese)[张燕萍,赵晓鹏,保石,罗春荣2010物理学报59 6078]
[9]Alici K B,Bilotti F,Vegni L,Ozbay E 2010J.Appl.Phys.108 083113
[10]Xu Y Q,Zhou P H,Zhang H B,Chen L,Deng L J 2011J.Appl.Phys.110 044102
[11]Bao S,Luo C R,Zhang Y P,Zhao X P 2010Acta Phys.Sin.59 3187(in Chinese)[保石,罗春荣,张燕萍,赵晓鹏2010物理学报59 3187]
[12]Ding F,Cui Y X,Ge X C,Jin Y,He S L 2012Appl.Phys.Lett.100 103506
[13]Wen Q Y,Zhang H W,Xie Y S,Yang Q H,Liu Y L 2009Appl.Phys.Lett.95 241111
[14]Ye Y Q,Jin Y,He S L 2010J.Opt.Soc.Am.B 27 498
[15]Huang L,Chowdhury D R,Ramani S,Reiten M T,Luo S N,Uaylor A J,Chen H T 2012Opt.Lett.37 154
[16]Liu N,Mesch M,Weiss T,Hentschel M,Giessen H 2010Nano Lett.10 2342
[17]Jiang Z H,Yun S,Toor F,Werner D H,Mayer T S 2011ACS Nano5 4641
[18]Wang J,Chen Y T,Hao J M,Yan M,Qiu M 2011J.Appl.Phys.109 074510
[19]Dai L,Jiang C 2009Opt.Express17 20502
[20]Aydin K,Ferry V E,Briggs R M,Atwater H A 2011Nat.Commun.2 517
[21]Lin C H,Chern R L,Lin H Y 2011Opt.Express19 415
[22]Hu C G,Li X,Feng Q,Chen X N,Luo X G 2010J.Appl.Phys.108 053103
