基于M－H抽样算法的贝叶斯Probit分位回归模型研究＊

朱慧明，李 荣，曾昭法，虞克明

（1.湖南大学工商管理学院，湖南长沙 410082； 2.湖南大学金融与统计学院，湖南长沙 410079；3.Brunel大学数学系，伦敦 UB8 3PH）

Probit模型广泛应用于经济布局、企业选址、交通问题、就业问题和购买决策等经济决策领域.在经典计量经济学模型中，因变量通常为连续变量，但在经济分析，如销售或购买某种商品、犯罪、迁移、生育和患病与否等，因变量只取两个值，可以用Probit模型（0或1）来度量经常面临选择问题，从而在可供选择的方案中做出决策.离散Probit选择模型在经济研究中大量应用，许多学者用Probit模型回归方法对实际问题进行分析.林相森，艾春荣（2008）［1］对中国居民医疗需求影响因素用有序的Probit回归模型进行分析；陈磊等（2009）［2］运用序次Probit回归模型对离散股票价格进行建模分析，结果表明该模型可反映价格离散特征；张欣［3］（2010）用Probit离散选择模型对船舶溢油事故的选择概率进行预测.Koenker和Bassett［4］于1978年提出了分位回归理论，不少学者把Probit均值回归模型推广到Probit分位回归模型，Delgado（2001）［5］从理论上证明了Probit分位回归的重抽样方法对参数最大得分估计方法的可行性，但此方法计算复杂，并且只能适用于低维小样本问题.Korads（2006）［6］把核密度方法推广到一般的Probit分位数回归，但核密度估计方法对扰动项分布的光滑性要求很强，同时表明当仿真样本数等于1 000时，很难去估计参数的标准差.Koenker（2005）［7］指出，选择光滑参数对最大得分函数的参数估计会产生较大的影响.Florios和Skouras（2008）［8］指出针对Probit分位回归的最大得分函数的优化问题，提出了混合整数规划来解决此问题，但仍然不能得到待估参数的统计性质.总之，对Probit模型进行建模分析，存在参数随机化条件下建模困难和参数求解的问题.

本文利用贝叶斯统计推断理论和分位回归技术对Probit模型进行分析，解决参数随机化条件下的Probit模型构建问题，对离散Probit模型分别用贝叶斯Probit分位回归模型与分位回归模型和光滑分位回归模型对参数估计比较分析，得到不同分位点模型参数的后验分布.

1 Probit分位回归模型

Probit离散选择回归模型在社会生活、经济、统计决策和数据挖掘中有着广泛的应用，Probit离散选择模型其具体形式如下：

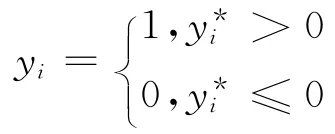
其中此处yi为第i个样本的指示变量，取值0或1，为潜变量，＝（x1，x2，…，xk），＝（β1，β2，…，βk），εi为随机扰动项，i＝1，2，…，n.

下面考虑选择yi＝1的概率.设F（ε｜x＝xi）表示给定x＝xi下随机扰动项的条件分布函数，从式（1）可知

从普通的Probit均值回归模型推广到一般的Probit分位回归模型过程中，待估参数随着分位水平的变化而改变，从而Probit分位回归模型可以更加详细地描述解释变量x对潜变量Y＊的条件分布的位置和形状的影响.

假设随机变量Y＊与解释变量向量x之间具有线性函数关系

其中x′＝（x1，x2，…，xk），β＝（β1，β2，…，βk）′，ε为概率分布函数F的随机扰动项.显然，对于给定的x′，随机变量Y＊的p分位数等于x′β＋F－1（p），即

不难看出，其等价形式为：

此处β（p）＝（β1（p），β2（p），…，βk（p））′，也就是说，β（p）与分位数p的取值大小有关.显然，对于不同的p值，可以得到相应的多个分位点的回归模型.给定一组观察值β（τ）的估计为：

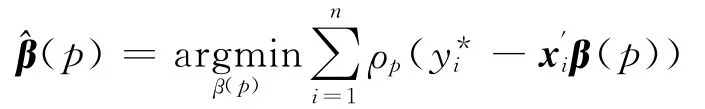
此处ρp（u）＝u（p－I（u＜0））为损失函数，I（u＜0）为示性函数；当u＜0时，I（ui＜0）＝1；否则，I（u＜0）＝0.由于β（p））等价于

在式（1）的条件下，可求得Probit分位回归参数估计形式如下：此处sgn（·）为符号函数.

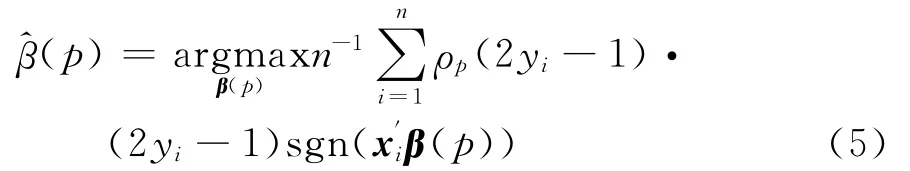
2 Probit分位回归模型的贝叶斯分析

非对称Laplace分布是应用贝叶斯方法分析Probit离散选择回归模型的重要工具.如随机变量y服从偏度参数p，尺度参数σ和位置参数μ的非对称Laplace分布［9］，其密度为：

记作Y～ALD（μ，σ，p）；特别地，当μ＝0，σ＝1时，记作Y～ALD（p）.

如ε～ALD（μ，σ，p），可得如下似然函数

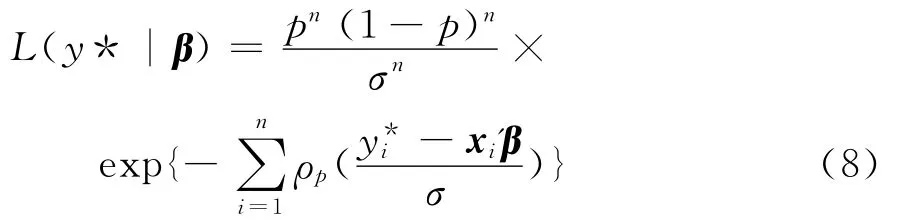
根据贝叶斯定理，可知待估参数β的后验分布

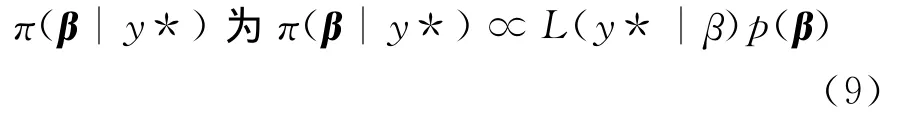
此处p（β）为β的先验分布.

本文只考虑ALD（μ，σ，p）分布σ＝1时的情形，给定一组数据y＝（y1，y2，…，yn）和分位数p值，可得Probit分位回归中待估参数β和潜变量Y＊的联合后验密度为：

此处p（β）为β的先验分布，I（.）为指示变量.

由于式（10）联合后验密度的分布的形式未知，所以直接抽样不可能完成，可以通过数据扩充来实现对β的抽样，可以把式（10）分解两个全条件后验分布可以完成.从式（10），可得Y＊的全条件后验密度为

当yi＝1时，y＊i左截断0；yi＝0时，y＊i右截断0.

由于直接对非对称Laplace分布抽样困难，利用非对称Laplace分布的性质，可以分解成两个常用的分布来完成上述抽样.文献［10］在对回归模型进行贝叶斯分位分析时，研究证明选择参数的先验信息为无信息先验分布，可以得到待估参数合适的后验分布.从式（10），可得β的后验密度为：

针对贝叶斯分位Probit回归模型参数后验分布的解析形式不确定的问题，采MCMC模拟解决贝叶斯估计过程中遇到的高维积分问题.利用M－H抽样模拟Markov链，此链的平稳分布可以近似看作模型参数的后验条件分布，用MCMC模拟得到的样本来估计模型的参数［11］.

为了使Markov链的平稳分布就是目标分布，接受概率通常选择为：

选择对称建议分布（proposal distribution）为q（β′，β）＝q（β，β′），此时α（β，β′）＝min｛1，π（β′｜y）／π（β｜y）｝.如果Markov在时刻t处于状态β，即β（t）＝β，则由q（.｜β）产生一个转移β→β＇；然后根据α（β，β′）决定是否转移.

假设给定初始值Θ（0）＝（y＊（0），β（0）（p）），并设（y＊（j－1），β（j－1）（p））为（y＊，β（p））的第j－1次抽样结果.则第j次抽样的过程包括以下两个步骤：

由上完成了一次M－H迭代过程，即完成了由（y＊（j－1）（p），β（j－1）（p））到（y＊（j）（p），β（j）（p））的转移；不断重复以上步骤直到链条达到稳定状态，经过t次迭代，可以得到（y＊（t）（p），β（t）（p））.

如果总共迭代N次，则获得如下迭代结果：

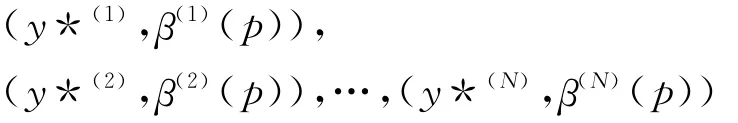
一般说来，在抽样过程的初始阶段，过程处于非平稳状态；因此，在估计模型参数时，去掉最初抽样的M个点｛（y＊（j），β（j）（p）），j＝1，2，…，M｝，利用随后N－M次迭代所获得的随机数，形成一个容量大小为N－M的样本｛（y＊（j），β（j）（p）），j＝M＋1，M＋2，…，N｝，据此求出β（p）的估计及其方差，即：

3 MCMC仿真分析

利用随机模拟生成服从Probit回归的200个数据，首先用这些数据来验证贝叶斯方法应用于Probit分位回归模型的有效性，然后把Probit分位回归（PQR）、光滑Probit分位回归（SPQR）［6］和贝叶斯Probit分位回归（BPQR）在0.5分位点进行参数估计结果的比较.实验数据的生成过程如下.

对于异方差模型：

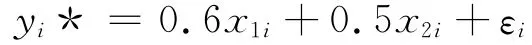
此处

选择先验分布为均匀分布，M－H抽样算法中的建议分布为指数分布，由M－H抽样可以模拟得到各个参数的边缘后验分布，把模型（13）用M－H抽样10 000次估计待估参数，得到β1和β2在0.05，0.10，0.25，0.75，0.90，0.95等6个分位点参数β1的动态迭代轨迹图（图1）、参数β2的动态迭代轨迹图（图2），从参数的迭代轨迹图可以发现马尔可夫链收敛，说明MCMC仿真过程是平稳的.

图1 不同分位数下参数β1动态迭代轨迹Fig.1 Dynamic iterative Chain track of theβ1 parameter in different quantiles

图3和图4分别给出不同分位数下参数后验分布的核密度估计曲线，从回归的后验分布密度图可以看出，其表现为比较平滑且呈钟型，说明M－H算法有效地模拟了模型中各参数的边缘后验分布.在低分位点，X对y的影响为负，在高分位点，X对y的影响为正，说明虽然y的取值只是两元，误差项不是标准的Laplace分布，但通过贝叶斯probit分位回归，可以得到在每个分位点的影响情况.

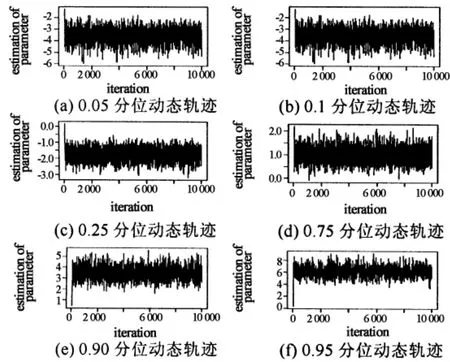
图2 不同分位数下参数β2动态轨迹Fig.2 Dynamic iterative Chain track of theβ2 parameter in different quantiles

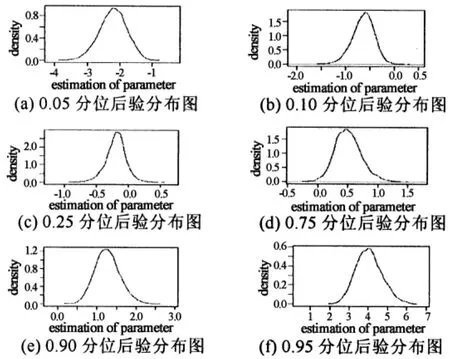
图3 不同分位数下参数β1的后验密度图（样本量10 000）Fig.3 Posterior density estimation of theβ1 parameter in different quantiles

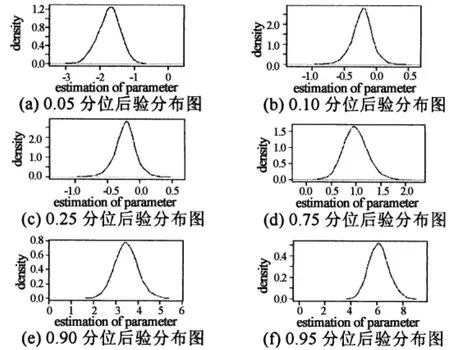
图4 不同分位数下参数β2的后验密度图（样本量10 000）Fig.4 Posterior dersity estimation of theβ2 parameter in different quantiles

在样本量分别为200，500和800的情形下，分别用PQR，SPQR和BPQR对模型（13）的参数进行估计，在0.5分位点，得到参数估计的偏差、单位均方误差（RMSE）和95%的置信区间如表1所示.

表1 参数估计的偏差、单位均方误差和95%的置信区间Tab.1 Biased，RMSE and the 95%confidance level of parameters estimation

4 结 论

本文针对Probit分位回归在参数随机化条件下的建模问题，利用非对称Laplace分布实现对Probit分位回归模型的贝叶斯推断.假定模型中的待估参数先验分布为无信息先验，利用M－H抽样算法得到待估参数的后验边缘分布，模拟在不同分位水平下参数的MCMC迭代动态轨迹图，参数的贝叶斯估计和边缘后验分布，各分位水平下参数的MCMC迭代轨迹是收敛的，说明M－H抽样很好地模拟了参数的后验边缘分布，各分位水平下参数的标准差比较小，且参数的后验密度呈钟型，贝叶斯Probit分位回归模型解决了因变量为离散变量时参数估计不确定问题.与传统的Probit分位回归方法相比，贝叶斯分位回归方法可以合理地解释Probit模型中参数随分位数变化的特点，得到更加准确有效的参数估计.

［1］ 林相森，艾春荣.我国居民医疗需求影响因素的实证分析－有序probit模型的半参数估计［J］.统计研究，2008，25（11）：40－45.LIN Xiang－sen，AI Chun－rong.Determinants of Chinese resident’s demand for medical care－an application of semiparametric estimation of ordered probit model［J］.Statistical Research，2008，25（11）：40－45.（In Chinese）

［2］ 陈磊，李平，曾勇.基于序次probit模型的离散股价研究［J］.系统工程学报，2009，24（5）：561－567.CHEN Lei，LI Ping，ZENG Yong.Research on discrete stock price based on ordered probit model［J］.Journal of Systems Engineering，2009，24（5）：561－567.（In Chinese）

［3］ 张欣.船舶溢油事故报告选择概率预测研究［J］.数理统计与管理，2010，29（2）：197－204.ZHANG Xin.Forecast of accident report choice probability in ship oil－spill emergency［J］.Journal of Applied Statistics and Management，2010，29（2）：197－204.（In Chinese）

［4］ KOENKER R，BASSETT G.Regression quantiles［J］.Econometrica，1978，46（1）：33－50.

［5］ DELGADO M A，RODRIGUEZ－POO J M，WOLF M.Subsampling inference in cube root asymptotics with an application to Manski’s maximum score estimator［J］.Economic Letters，2001，73（2）：241－250.

［6］ KORDAS G.Smoothed binary regression quantiles［J］.Journal of Applied Econometrics，2006，21（3）：387－407.

［7］ KOENKER R.Quantile regression［M］.New York：Cambridge University Press，2005.

［8］ FLORIOS K，SKOURAS S.Exact computation of max weighted score estimators［J］.Journal of Econometrics，2008，146（1）：86－91.

［9］ YU K，MOYEED R A.Bayesian quantile regression［J］.Statistics and Probability Letters，2001，54（4）：437－447.

［10］YU K，STANDER J.Bayesian analysis of a tobit quantile regression model［J］.Journal of Econometrics，2007，137（1）：260－276.

［11］曾慧芳，朱慧明，李素芳，等.基于MH算法的贝叶斯分位自回归模型［J］.湖南大学学报：自然科学版，2010，37（2）：88－92.ZENG Hui－fang，ZHU Hui－ming，LI Su－fang，et al.Bayesian inference on the quantile autoregressive models with metropolis－hastings algorithm［J］.Journal of Hunan University：Nature Sciences，2010，37（2）：88－92.（In Chinese）