自适应半主动悬架系统控制策略＊

郭孔辉，余五辉，章新杰，†，马芳武，赵福全

（1.吉林大学汽车仿真与控制国家重点实验室，吉林长春 130022； 2.湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙 410082； 3.浙江吉利汽车研究院，浙江杭州 311228）

现代汽车正朝着安全、舒适、节能、环保、智能化的方向发展，人们对汽车的舒适性和整体品质的追求日益提升，半主动悬架能很好地兼顾舒适性、操纵稳定性，且辅助能量需求小，是当前关注的热点，国内外学者对半主动悬架的控制策略做了较多研究，其中基于天棚阻尼原理的半主动控制简单有效，易于实现，具有一定优势［1－3］.目前的天棚阻尼控制算法主要有“ON－OFF”和“CVD”两种模式.

文献［4］在频域分析了Sky－Hook，ADD，Mixed SH－ADD几种“ON－OFF”控制算法，并得出在系统高频区和低频区，SH－ADD算法都能有效衰减振动.文献［5］在SH－ADD算法基础上提出了一种单个传感器控制策略，它兼顾了控制效果与成本，能有效减振（虽然没有SH－ADD算法效果好），而且可以节省4个传感器，大幅度节省了控制成本.Daniel和Douglas在文献［6］中提出了连续阻尼控制天棚算法，并把“ON－OFF”和“CVD”两种控制模式进行比较，得出后者能更好地提高汽车的行驶平顺性，但是并没有对控制系统进行鲁棒分析或自适应优化，当汽车在复杂工况下运行时，不能很好地表现出其性能.Kim和Lee在文献［7］中提出了将减振器分为Comfort，Auto以及Sport 3个模式，以满足不同车主在不同行驶工况下的不同要求，目前很多高档车都采用了这一思路.

以上各种算法都采用单一的控制参数，但汽车行驶的工况复杂，很难找到一组能满足所有工况的控制参数.本文首先用悬架动行程均方值大致估计了路面不平度等级；其次提出一种基于路面辨识的自适应型半主动悬架控制策略；然后采用遗传算法对不同工况时的控制参数进行离线优化；最后将优化后的参数用于在线系统.

1 7自由度半主动悬架整车建模

在进行半主动和主动悬架控制策略对平顺性改善的研究时，一般采用1／4车辆模型，忽略轮胎阻尼，将悬架弹簧近似为线性元件［8］.本文考虑了路面不平引起的车身姿态的变化，因此采用7自由度车辆模型.同时考虑到车辆在很差路面上行驶时，悬架的限位作用会使其刚度表现出较大的非线性，这样就不能将悬架弹簧近似为线性元件.因此本文建立考虑悬架限位的非线性整车车辆模型，用Fs表示该车辆悬架刚度和动行程引起的作用力，其值可通过试验特性曲线查表得到，具体刚度特性见图1，图中拉伸时的刚度突变是由减振器的刚性限位引起的，压缩时刚度变化是由缓冲块作用引起的.如图2所示，悬架与车身连接处的垂向位移分别为Z1，Z2，Z3，Z4；Φ，Θ分别表示质心处的俯仰角和侧倾角；a，b分别表示质心到前后轴的距离；c为轮距.根据运动关系可以得到式（1）：

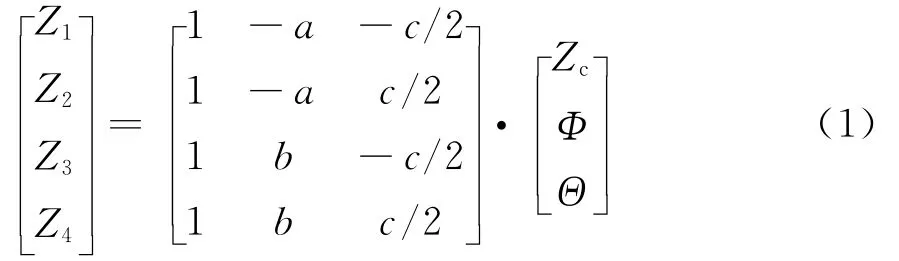
悬架变形产生的作用力按式（2）计算：

式中i＝1，2，3，4分别表示左前、右前、左后、右后4个悬架与车身连接点.FSi表示4个位置处的弹簧力，可通过查表获得，Fami表示4个位置处的减振器力，采用改进天棚阻尼控制算法如公式（3）所示：

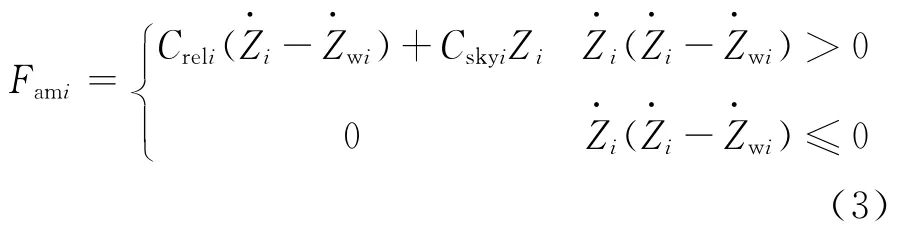
其中Creli，Cskyi分别为单个减振器天棚控制算法中的被动阻尼系数和天棚阻尼系数.

图1 试验得到的前悬架刚度Fig.1 Front suspension stiffness property

图2 7自由度整车模型Fig.2 Scheme of the 7DOF full car model

对上面的方程组整理可得整车7自由度垂向振动模型，结果如式（4）和（5）：

2 半主动悬架系统参数优化

上述半主动控制逻辑中每个减振器处都有Crel，Csky2个参数（共8个参数）对控制系统的效果影响很大，为了能够在不同路况下达到最优控制效果，用Simulink搭建上述半主动整车模型，考虑车辆前后轴轴荷的差异而忽略左右轮轮荷的差异，令Crelf＝Crel1＝Crel2，Crelr＝Crel3＝Crel4，Cskyf＝Csky1＝Csky2，Cskyr＝Csky3＝Csky4，这样需要优化的为Crelf，Crelr，Cskyf，Cskyr4个参数.将这4个参数写成向量形式，令x＝［CrelfCrelrCskyfCskyr］，并采用遗传算法对这个参数进行优化.

2.1 目标函数

目标函数的定义应该同时考虑行驶平顺性和操纵稳定性.参考汽车平顺性试验方法（GB／T 4970－2009）中随机路面平顺性评价指标的定义，同时考虑垂向、俯仰、侧倾3个方向的振动，由于垂向、俯仰，尤其是俯仰运动是引起人们晕车、呕吐的主要因素，故在平顺性评价中赋予其更大的权重.本文车辆的操纵稳定性是通过车轮动载荷来进行评价的.车身垂向加速度Z¨c、俯仰加速度Φ¨、侧倾加速度Θ¨是评价车辆乘坐舒适性的重要依据.为了综合考虑这三者的影响，利用统一的公式综合评价，见式（6）：

为使在行驶过程中能够，车辆具有良好的行驶稳定性，要求车辆的动载荷尽量小.综合考虑4个车轮动载荷Ti（i＝1～4），利用统一的公式评价，见式（7）：

为了使平顺性和行驶稳定性两个指标在一个数量级上，具有可比性，参考文献［9］，修正行驶稳定性目标函数，见式（8）：

综合式（6），式（8）得到一个总体的目标函数，见式（9）：

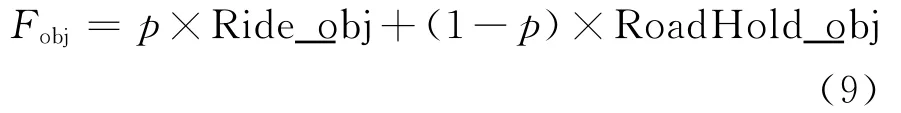
其中p为平顺性权衡系数，在0～1间取值.p值的大小根据车辆行驶状态进行选择，在舒适模式，p取较大值以便获得更好的行驶平顺性.相反，在运动模式下，p取较小值以便得到更好的操纵稳定性.

2.2 约束方程

优化时需要兼顾减振器的实际条件和行车安全性［10］.考虑减振器实际情况，约束方程如式（10）：

另外，从行车安全性出发：悬架动行程允许范围由结构空间定为±100mm；轮胎动位移的允许范围则根据对轮胎的接地要求而定.如以轮胎不离地为极限，则要求轮胎最大动负载小于轮胎静态负载，根据系统输出的高斯分布特性，即可确定其目标均方根值.如果设定极限值在±3σ，也就是说输出达到极限位置的可能性很小（时域内概率为0.3%），则要求轮胎动位移均方根值和悬架动行程均方根值满足式（11）和（12）：

2.3 优 化

当车辆行使在良好路面上并且车速低于100 km／h时，可更多地考虑汽车的舒适性，令p＝0.7，此时用遗传算法工具箱进行优化，可得到控制参数最优值：x＝［90 741 659 985 090］.同样方法对不同路面输入，不同车速进行优化，结果如表1所示.

表1 不同路面、不同权系数p的优化结果Tab.1 The control parameters under different weight pand road

当路况很差时，悬架动行程过大，会经常撞击限位块，导致舒适性变差，同时轮胎动载荷过大，也会导致轮胎脱离地面，安全性变差.这时应当将减振器调硬，故取p＝0.3.

表2 很差路面、不同车速的优化结果Tab.2 The optimal control parameters for poor road

根据以上优化结果，将悬架控制定义为Comfort，Sport，Safe 3个模式.取Comfort模式下x＝［800，400，5 800，4 900］，Sport模式下x＝［1 500，1 200，4 200，3 600］，Safe模式下x＝［2 600，2 200，5 100，4 200］.

3 自适应控制策略

3.1 路面识别

［11］，可得到悬架动行程均方值与路面等级、车速等的关系如式（13）所示：

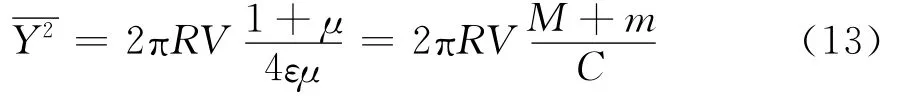
式中M，m分别为簧载质量与非簧载质量；C为阻尼系数；V为车速；R为路面等级系数，易得（14）式：

不同R值对应不同路面等级关系如下：

很差路面R≥1（cm2·circle／m）

较差路面0.01＜R＜1（cm2·circle／m）

良好路面R≤0.01（cm2·circle／m）

式中q＝lgR，flag＝1，2，3分别对应良好路面、较差路面、很差路面.

通过式（15）可大致估计路面等级.应该指出式（13）是在线性1／4车辆模型中推导出来的，本文将其用于整车的路面不平度等级的区分，需要建立与其等效的1／4车模型，然后利用式（15）进行估计.

参考文献［12］，建立一段包含ISO A，C，E 3个级别路面的随机路谱（A，C每个级别各100m，E级40m），来检验公式（15）中提出的路面不平度等级识别效果.其中E级路段车速为36km／h，A，C路段车速都为90km／h，这样每段的行车时间都为4 s，如图3所示.

图4为路面识别效果，结果说明系统能很好识别路面，识别历时1s左右，但是由E级路面到A级路面时，识别时间达到2s，是因为由坏路面上的大振幅运动，衰减到好路上小振幅运动需要一段时间.实际的在线系统识别时间要由实车上传感器的采样频率、控制器的数据处理以及存储能力决定.

图3 仿真路面Fig.3 Road input

图4 路面识别效果Fig.4 Result of road identification

3.2 控制模式的切换

对于特定路面（不是很差路面），选定一个车速阈值VF，当车速低于该阈值时应更多地考虑舒适性，把控制参数调为Comfort模式；当车速高于VF时应更多考虑操纵稳定性，把控制参数调为Sport模式.当路面很差时，应更多考虑行驶安全性，把控制模式调为Safe模式.下面是需要考虑操纵性路面上VF值的选取，如表3所示.

表3 不同路面VF的选取Tab.3 VFfor different roads

4 仿真分析

4.1 仿真模型

本文基于Simulink建立了被动悬架系统、CVD系统和自适应CVD系统的7自由度车辆模型，并通过对不同行驶工况的仿真对比几个控制系统的优缺点.模型参数见表4.

表4 整车系统参数Tab.4 Parameters of a entire car

4.2 仿真结果

下面以车辆簧载质量质心处加速度（Sprung mass vertical accel）均方根值来评价车辆的舒适性，以车轮动载荷（Tire dynamic force）的均方根值与车轮静载的比值η＝0.25×∑（RMS（Ti）／F0i），来评价车辆的操纵稳定性.表5，表6列出了不同行驶工况下，3种不同悬架系统的性能对比.

表5 不同行驶工况下η值的比较Tab.5 Comparision ofηunder different conditions

表6 不同工况下RMS（）的比较Tab.6 Comparision of RMS（）under different driving conditions

表6 不同工况下RMS（）的比较Tab.6 Comparision of RMS（）under different driving conditions

行使状况自适应CVD传统CVD 被动悬架好路中低速0.170 5 0.230 5 0.351 0好路高速0.279 9 0.262 9 0.365 2较差路低速0.510 7 0.616 1 0.825 9较差路高速0.786 0 0.734 2 0.997 8很差路低速1.121 5 0.973 3 1.053 8

由表5，表6可以看出，车辆在好路中低速行驶以及较差路面上低速行驶时，自适应CVD能牺牲一部分操纵稳定性来减小车身的振动；而在好路以及较差路面高速行驶时，自适应CVD能牺牲一部分平顺性来提高车辆的操纵稳定性；同时在很差路面上行驶时，自适应CVD能很好地保证安全性.简而言之，相对传统CVD、被动悬架，自适应CVD具有以下优势：1）当车速较低车辆操纵稳定性较好时，能有效提高汽车的舒适性；2）当车速较高汽车操纵稳定性较差时，能有效提高系统的操纵稳定性；3）在很差路面上行驶时，能在保证行车安全的基础上提高舒适性.

值得指出的是表5中加星号的部分，它表明传统CVD悬架在差路上行驶以及以较高车速行驶于较差路面上时，其车轮动载不满足约束条件式（10），此时车轮的抓地能力会很差，导致安全性变差.而且此时悬架动行程过大，会经常撞击限位块，导致舒适性变差，这一点表6中并没表现出来，主要是因为此时，传统CVD悬架已有一定概率撞击限位块，导致其加速度响应局部峰值很大，而其均方根值并未增加多少，但这时局部的冲击感带来的平顺性恶化会比均方根值更多.换句话说，这时加速度均方根值并不能很好地评价平顺性.

此外，为了评价自适应CVD系统的低频响应特性，以及CVD控制算法对由路面不平引起的俯仰侧倾的控制效果.定义如下工况，车速36km／h，车辆左侧通过图5所示的凹坑，这样车辆的俯仰，侧倾，垂向运动都能很好地表现出来.车辆的侧倾角加速度、俯仰角加速度和垂向加速度仿真结果如图6～8所示.通过比较可以得出，自适应半主动控制相对被动最优悬架，低频响应有了明显的改善.

图5 凹坑路面Fig.5 Chuck hole

图6 车辆单侧通过凹坑的侧倾角加速度Fig.6 Roll angular acceleration when subjected to the“chuck hole”road disturbance

图7 车辆单侧通过凹坑的俯仰角加速度Fig.7 Pitch angular acceleration when subjected to the“chuck hole”road disturbance

图8 车辆单侧通过凹坑的垂向加速度Fig.8 Vertical acceleration when subjected to the“chuck hole”road disturbance

5 结 论

在Simulink中建立了考虑悬架限位的带CVD控制算法的7自由度整车模型，并利用Matlab中的遗传算法工具箱对模型中的参数进行离线优化，得到3组不同的控制系统反馈参数，对应这3组参数将控制系统分为Comfort，Sport，Safe 3个控制模式.

对不同路面输入悬架系统的响应进行了批量仿真，得到了一种路面不平度等级的识别方法，并设计了一种路面与车速自适应的半主动减振器控制逻辑.

仿真结果表明本文的控制方案能更好地权衡舒适性、操纵稳定性和安全性，自动调整控制参数，提高了汽车对复杂行驶工况的适应能力，可以提高汽车的整体品质.

参考文献

［1］ CAO D P，SONG X B，AHMADIAN M.Editors’perspectives：road vehicle suspension design，dynamics，and control［J］.Vehicle System Dynamics，2011，49（1／2）：3－28.

［2］ PAZOOKI A，RAKHEJA S，CAO D P.Modeling and validation of off－road vehicle ride dynamics［J］.Mechanical Systems and Signal Processing，2012，28：679－695.

［3］ GEORGIOU G，VERROS G，NATSIAVAS S.Multi－objective optimization of quarter－car models with a passive or semiactive suspension system［J］.Vehicle System Dynamics，2007，45（1）：77－92.

［4］ SERGIO M，CRISTIANO S.A single－sensor control strategy for semi－active suspensions［J］.IEEE Transactions on Control Systems Technology，2009，17（1）：143－152.

［5］ MILANO P，VINCI P.Acceleration－driven－damper（ADD）：an optimal control algorithm for comfort－oriented semi－active suspensions［J］.ASME，2005，127：218－229.

［6］ DANIEL S M，DOUGLAS E Z，ALLAN K A P.Optimization of a vehicle suspension using a semi－active damper［C］／／SAE Paper.2000－01－3304.

［7］ KIM W，LEE J，YOON S，et al.Development of mando’s new continuously controlled semi－active suspension system［C］／／SAE Paper.2005－01－1721.

［8］ POUSSOT－VASSAL C，SPELTA C，SENAME O，et al.Survey and performance evaluation on some automotive semi－active suspension control methods：a comparative study on a single－corner model［J］.Annual Reviews in Control，2012，36：148－160.

［9］ CAPONETTO R，DIAMANTE O，FARGIONE G，et al.A soft computing approach to fuzzy sky－hook control of semiactive suspension［J］.IEEE Transactions on Control Systems Technology，2003，11（6）：786－798.

［10］喻凡，郭孔辉.自适应悬架对车辆性能改进的潜力［J］.中国机械工程，1988，9（6）：67－69.YU Fan，GUO Kong－hui.The potential of an adaptive suspension to improve vehicle performance［J］.Chinese Journal of Mechanical Engineering，1988，9（6）：67－69.（In Chinese）

［11］郭孔辉.汽车振动与载荷的统计分析及悬挂系统参数的选择［J］.汽车技术，1976：1－15.GUO Kong－hui.Statistic analysis of vehicle vibration and its application to suspension system design［J］.Automobile Technology，1976：1－15.（In Chinese）

［12］刘献栋，邓志党，高峰.公路路面不平度的数值模拟方法研究［J］.北京航空航天大学学报，2003，19（2）：843－846.LIU Xian－dong，DENG Zhi－dang，GAO Feng.Research on the method of simulating road roughness numerically［J］.Journal of Beijing University of Aeronautics and Astronautics，2003，19（2）：843－846.（In Chinese）