加权p，q对称熵损失下一类指数分布族的Bayes估计

王兰

（中国矿业大学理学院，江苏徐州 221116）

加权p，q对称熵损失下一类指数分布族的Bayes估计

王兰

（中国矿业大学理学院，江苏徐州 221116）

在一种新的加权p，q对称熵损失函数下，研究了一类指数分布族参数的Bayes估计及其可容许性，得到了可靠度的Bayes估计的一般形式与精确形式，并讨论了一类形如cT+d的Bayes估计的可容许性.

加权p，q对称熵损失函数；Bayes估计；可容许性

1 引言

在现代生产、生活中越来越多的产品要求可靠性指标，为此我们需要对产品进行可靠性测试.然而指数分布在排队论和可靠性理论中有着广泛的应用，如各种电子元件的寿命、电话的通话时间、候车等待时间等问题都可认为服从指数分布.

关于可靠度的估计，近年来用Bayes方法已取得了一些进展，如杜宇静、赖民[1]提出了q对称熵损失函数并讨论了指数分布在此损失函数下的最小风险同变估计、Bayes估计和最小最大估计，并讨论了容许性问题.杜宇静、孙晓祥、尹江艳[2]讨论了指数分布在p，q对称熵损失函数下的最小风险同变估计、Bayes估计和最小最大估计，并讨论了容许性问题.徐宝、宋立新[3]讨论了加权平方损失函数下刻度指数分布族刻度参数的最小同变估计.徐宝、张洪刚[4]讨论了在刻度平方损失函数下，一类指数分布族参数的估计.李俊华、钟太勇[5]讨论了熵损失函数下指数分布参数的估计.史晓明、蔡春娟[6]讨论了在对称熵损失函数下一类指数分布族的Bayes估计及可容许性.

本文主要讨论在加权p，q对称熵损失函数下一类指数分布族的Bayes估计及可容许性.

a=0， T(b)=+∞，又假设θ＞0，T'(x)＞0，故T(x)严格单调递增.

我们在加权p，q对称熵损失函数

下面考虑参数θ的估计问题.

这里δ是待估参数θ的估计量.容易看出损失函数（1）关于待估参数与其估计量是p，q对称的，也就是交换二者以及p，q的位置，不影响损失函数的形式.而且当p=q时，损失函数（1）具有与平方损失函数以及绝对损失函数一样的对称性.且易知此损失函数关于δ是严格凸的，并且在δ=θ处取得唯一最小值[7].

2 参数θ的Bayes估计[8]

这一部分在贝叶斯框架下，利用损失函数（1）来研究θ的估计及其性质.下面定理给出参数θ的Bayes估计[9].

定理1对于任何先验分布，在损失函数（1）下，θ的Bayes估计为

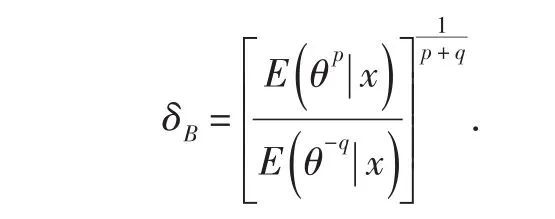
证明对损失函数，令δ(X)为θ的任一估计，其Bayes风险为

要使R(θ,α)达到最小，只需使后验风险达到最小，由于

上式右端关于δ求导并令其等于0，解得

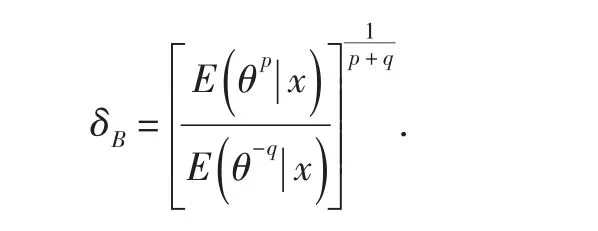
下面讨论在给定先验分布π()θ后，参数θ的精确Bayes估计形式及其性质.

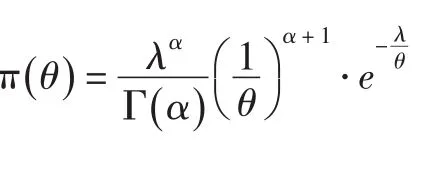
并且是θ的可容许估计.

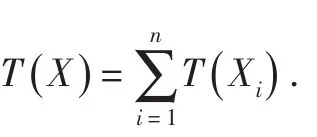
可见后验分布服从ΙΓ(n+α,λ+T(X))，从而有

从而

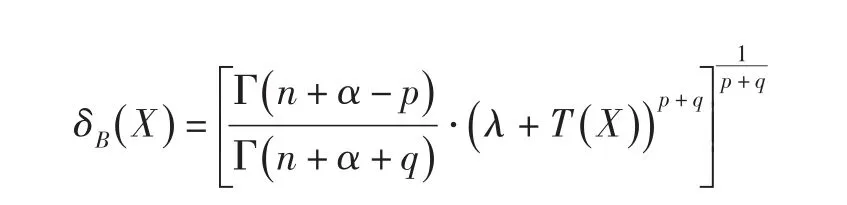
引理1在所给定的Bayes决策问题中，若对给定的先验分布π(θ)，θ的Bayes估计是唯一的，则它是可容许估计.

由加权p，q对称熵损失函数（1）的严格凸性，易知其Bayes估计必唯一，故由引理1可知，Bayes估计δB(X)亦是可容许估计.

3 估计量cT+d的容许性讨论[8]

由以上讨论可以看出，参数θ在损失函数（1）下的可容许Bayes估计具有形式cT+d.下面讨论参数θ的几个形如cT+d的估计的容许性与不可容许性.

定理3当0＜c≤c*，d＞0时，估计量cT+d是可容许的.

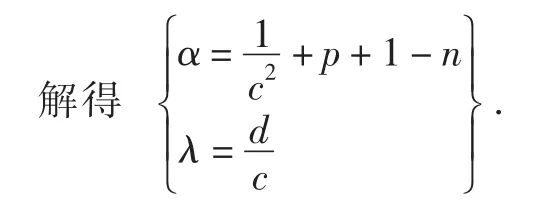
定理4若c=0，d＞0，则在损失函数（1）下，估计量d是参数θ的可容许估计.

证明如若不然，则必存在某个估计δ(X)优于δB(X)=d，即

（1）对任意θ＞0，有0≤R(θ,δ0(X))≤R(θ,d)；

（2）且对某些θ，有R(θ,δ0(X))＜R(θ,d).

当θ=d时，有0＜R(d,δ0(X))≤R(d,d)≤0，而损失函数L(θ,δ)非负，有L(d,δ0(X))=0，故δ0(X)=d，从而d是参数θ的可容许估计.

[1]杜宇静，赖民.q对称熵损失函数下指数分布的参数估计[J].吉林大学学报：理学版，2005，43（1）：10-15.

[2]杜宇静，孙晓祥，尹江艳.p，q对称熵损失函数下指数分布的参数估计[J].吉林大学学报：理学版，2007，45（5）：764-766.

[3]徐宝，宋立新.加权平方损失下一类指数分布族刻度参数的估计[J].黑龙江大学自然科学学报，2009，26（6）：766-799.

[4]徐宝，张洪刚.一类刻度指数分布族参数的Bayes估计[J].佳木斯大学学报：自然科学版，2009，27（4）：611-612.

[5]李俊华，钟太勇.熵损失函数下指数分布参数的估计[J].四川理工学院：自然科学版，2010，23（3）：278-279.

[6]史晓明，蔡春娟.对称熵损失函数下一类指数分布族的Bayes估计[J].通化师范学院学报，2011，32（4）：15-16.

[7]徐宝.寿命产品可靠度的贝叶斯估计[J].统计与决策，2011，4：153-154.

[8]茆诗松.贝叶斯统计[M].北京：中国统计出版社，1999.

[9]王兰.加权p，q对称熵损失下Reyleigh分布参数倒数的Bayes估计[J].贵州师范学院学报，2012，3：1-3.

[10]茆诗松，王静龙，濮小龙.高等数理统计[M].北京：高等教育出版社，2006.

Bayes Estimation on a Class of Exponential Distribution Family Under a Weighted p,q Symmetric Loss Function

WANG Lan
(School of Science,China University of Mining and Technology,Xuzhou 221116,China)

Under a weighted p,q symmetric loss function,this paper studies the Bayes estimation and admissibili⁃ty of the parameters on a class of exponential distribution family.And the paper gets the general form and exact form of the reliability’s Bayes estimation and discusses the admissibility of a class of cT+d form.

weighted p,q symmetric loss function；Bayes estimation；admissbility

O212.8

A

1008-2794（2013）04-0013-04

2013-03-15

王兰，中国矿业大学理学院概率论与数理统计专业研究生，E-mail：Wanglan4095@126.com.