核主成分法的应用

谷伟伟，王兰，芦凌飞

（中国矿业大学理学院，江苏徐州 221116）

核主成分法的应用

谷伟伟，王兰，芦凌飞

（中国矿业大学理学院，江苏徐州 221116）

分别利用主成分法和核主成分法，对2010年江苏省13个市的旅游业发展情况进行对比分析，发现核主成法分析的结果更加合理，并分析了原因，最后对江苏未来的旅游业发展提出了建议，供有关部门参考.

主成分分析；核主成分分析；SPSS；Matlab

主成分分析是重要的多元统计方法，它的应用一直是个热点问题.文献[1]从矩阵的特征值和特征向量出发，揭示了主成分分析和奇异值分解的关系，并给出了一个物理应用.文献[2]、[3]给出了主成分法在人脸识别中的应用.文献[4-10]给出了核主成分分析在不同领域中的应用，但是都忽略了相关结论的证明，而且也没给出Matlab算法.本文首先给出核主成分模型中相关结论的证明，然后用Matlab算出综合得分，最后和用SPSS算的主成分分析结果相对比，发现核主成分分析的结果较好，提高了综合评价的合理性.

1 预备知识

1.1 主成分模型

设有n个样品，每个样品观测p个变量，这p个变量具有较强的相关性.为了消除量纲不同造成的影响，将样本观测数据进行标准化处理的变量为X=(x1,x2,…,xp)′，其相关矩阵R的秩为r.

设λ1,λ2,…,λr,0,…,0为R的p个特征值，不失一般性λ1≥λ2≥…≥λr＞0.

设主成分Y=(y1,y2,…,yp)′，则主成分模型为Y=L′X，且LL′=Ip.

即

1.2 核主成分模型

于是，我们有

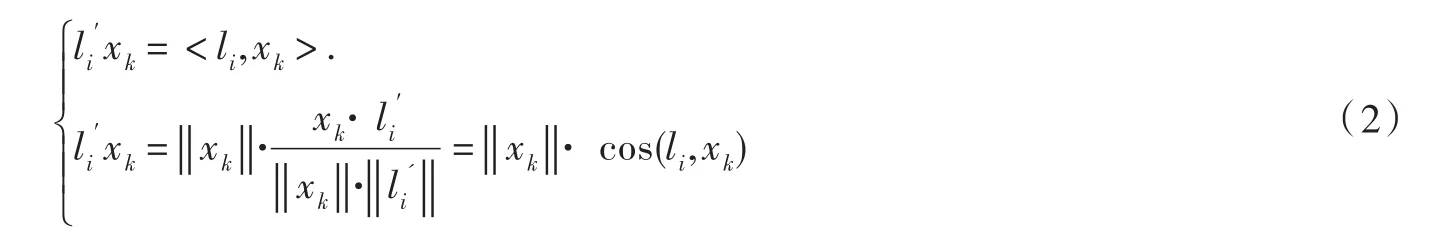
（2）式说明主成分是样本和特征向量的内积，或者是样本在特征向量上的投影.

设原始数据的样本为x1,x2,…,xn.xk∈Rp,k=1,2,…,n（即p个变量，n个样本），对数据进行标准化后

作一个映射ϕ，ϕ:Rp→F，进而空间F中的样本为ϕ(x1),ϕ(x2),…,ϕ(xn)，则协方差阵为

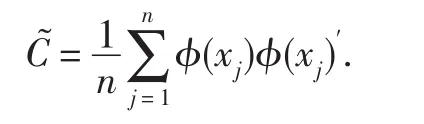
对（3）式两边同时作内积有

令kij=＜ϕ(xi),ϕ(xj)＞，α=(α1,α2,…αn)′，于是

对于（4）式左边，

对于（4）式右边，可以同理算出，这里不再赘述.

所以nλKα=K2α.所以α为K的属于特征值nλ的特征向量.

最后我们算出F空间中的主成分，即用F中的样本和特征向量v作内积.设第k个主成分记为tk，则

其中，vk表示的第k个特征向量.

由于ϕ是未知的，因此＜ϕ(xi),ϕ(x)＞不好求，这里用核函数来代替内积，即

K=(Kij)=[s＜xi,xj＞+c]d，s,c,d的选取要结合经验，见文献[11].

2 实例分析

本文选取的数据来自《2011中国区域经济统计年鉴》中6个旅游指标，具体指标如下：

x1—接待入境旅游者人数（万人次）；x2—接待外国人数（万人次）；x3—国际旅游外汇收入（万美元）；x4—国内旅游人数（万人次）；x5—国内旅游收入（亿元）；x6—星级饭店（个）.这6个指标都是正向化指标.

为了消除量纲的影响，我们对原始数据进行标准化，标准化变量为ZX1～ZX6（见表1）.经过SPSS计算，KMO值为0.807＞0.6，Bartlett球形检验值为0.000，说明适合进行主成分分析.

最大特征根为5.563，方差贡献率为92.717%.成分矩阵和成分得分系数阵见表2.下面用核主成分法分析.采用核函数Kij=[＜xi,xj＞]3，A是标准化后的矩阵（见表1）.进而求出K的特征值和特征向量，即eig（K），[v，d]=eig（K）.经计算，K的最大特征值为2.9764，特征贡献率为98%.将以上两种方法的计算结果放在一起对比分析，见表3.

表1 标准化后的数据

3 分析

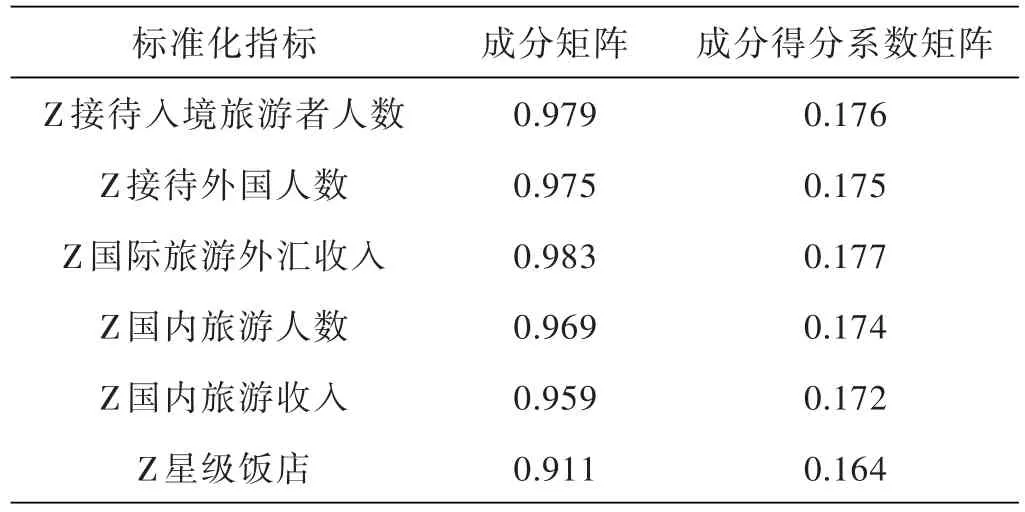
表2 成分矩阵和成分得分系数阵

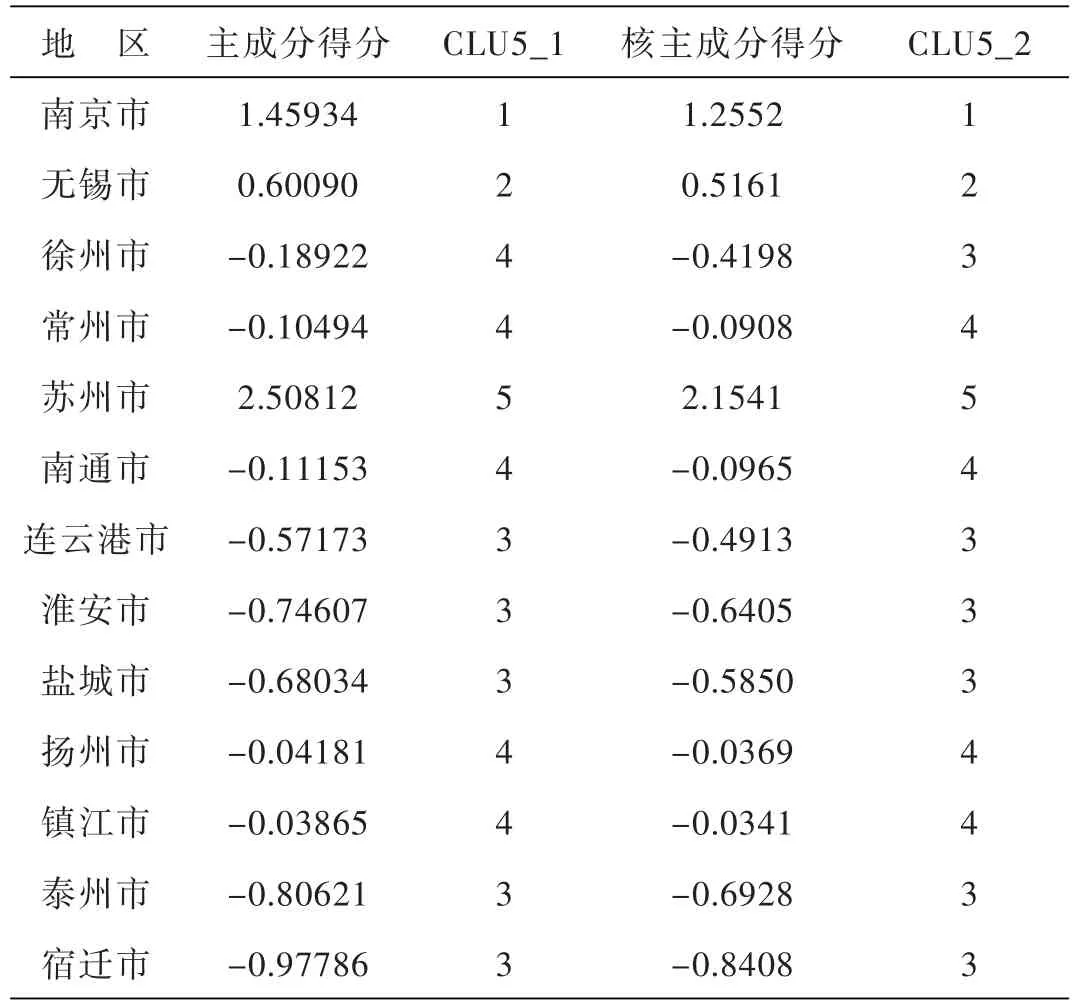
表3 两种方法的结果对比

CLU5表示用聚类方法将样本分为5类. CLU5-1是主成分法分类的结果；CLU5-2是用核主成分法分类的结果.

经过对比我们发现，主要的问题出在徐州的得分和排名上.从客观条件上分析：扬州、镇江、常州地处长江中下游，许多风景名胜和旅游城镇都因江而立，因江而兴.扬州是中国历史文化名城，有很多历史文化古迹，另外，古运河旅游线是江苏省“十五”期间重点开发的8条旅游线路之一，运河对扬州、镇江的城市景观和整体旅游业发展都有强大的带动作用.常州位于苏南，受到上海的辐射带动作用，经济发达，旅游业的基础配套设施比较齐全，如星级宾馆的数量比较多，游乐场也会相对多些.总体而言，扬州、镇江、常州的自然风景优美，旅游资源丰富，将它们分在一起是合理的.而徐州是重要的交通枢纽，它的重工业比较发达，污染严重.它的旅游业主要是文化旅游，自然风景不是很多，这和苏北的其他4个城市接近，因此，将徐州和淮安、泰州这些城市归在一起比较合适.

之所以出现上述情况，是因为主成分的方差贡献率为92.717%，而核主成分的方差贡献率为98%，核主成分的降维效果很显著，提取的信息较多.

4 建议

江苏旅游业发展的主要问题是不均衡.苏南的旅游业发展水平最高，苏中次之，苏北最低.

对于苏北：苏北旅游业和苏南地区相比，存在较大差距，主要是苏北旅游资源开发落后.但是苏北的旅游业潜力很大，苏北5市是江苏省旅游资源的富集区，集中了两汉文化、山水海滨、生态湿地、珍稀动物、名人名泉和淮扬美食等品牌资源.因此，要整合苏北的互补性旅游资源.

对于苏中、苏南：建议加大资金和科技投入，大力改善环境.

[1]Jonathon Shlens.A Tutorial on Principal Component Analysis[EB/OL].[2012-12-01L]http://wenku.baidu.com/view/a1f5ff4733687e21af45a9bf.html. 2009,4.

[2]Rajkiran G.,Asari Vijayan K.An improved face recognition technique based on modular PCA approach[J].Pattern Recognition Lett,2004,25(4):429-436.

[3]Yang,Jian,Zhang avid.Two-dimensional PCA:A new approach to appearance-based face representation and recognition[J].IEEE Trans Pattern Anal Machine Intell,2004,26(1):131-137.

[4]李磊，金菊良，梁忠民.核主成分分析的参数优化及其在水资源利用综合评价中的应用[J].水利水电科技进展，2009，29（4）：36-38.

[5]肖慧，刘苏东，黄小燕，等.基于核主成分的神经网络集合预报建模研究[J].计算机仿真，2010，27（12）：163-166.

[6]陈祥涛，张前进.基于核主成分分析的步态识别方法[J].计算机应用，2011，31（5）：1237-1241.

[7]吕薇，王新峰，孙智信.基于核主成分分析的高校科技创新能力评价研究[J].国防科技大学学报，2008，30（3）：81-85.

[8]程艳秋，迟国泰.基于核主成分分析的生态评价模型及其应用研究[J].中国管理科学，2011，19（3）：182-190.

[9]李明月，任九泉.基于核主成分分析和加权聚类分析的综合评价方法[J].统计与决策，2010，16：158-160.

[10]徐义田，王来生.核主成分分析在企业经济效益评价中的应用[J].数学的实践与认识，2006，36（1）：35-38.

[11]杨道军.核主成分分析法在生态经济可持续发展评价中的应用[J].环境科学与技术，2007，30（12）：91-93.

The Application of Kernel Principal Component Analysis

GU Wei-wei,WANG Lan,LU Ling-fei
(School of Science,China University of Mining and Technology,Xuzhou 221116,China)

In this paper,principal component analysis method and kernel principal component analysis method are used to research tourism development of thirteen cities in Jiangsu Province in 2010.The result shows that the kernel principal component analysis result is more reasonable,and the reasons are analyzed.Lastly,by using statistics analysis,some suggestions about future tourism development of Jiangsu Province are put forward for some departments.

principal component analysis;kernel principal component analysis;SPSS;Matlab

O153.5

A

1008-2794（2013）04-0020-04

2013-03-18

谷伟伟，硕士研究生，研究方向：多元统计分析，E-mail：864037364@qq.com.