控制不稳定的离散混沌系统

李昕，钱素平

（常熟理工学院数学与统计学院，江苏常熟 215500）

控制不稳定的离散混沌系统

李昕，钱素平

（常熟理工学院数学与统计学院，江苏常熟 215500）

利用一种不需要任何调节参数的控制方法，对离散的Hénon-like系统进行控制，将其稳定在固定点处.最后给出数值模拟的控制效果.

离散Hénon-like系统；混沌控制；反馈控制

1 引言

一直以来，由于混沌系统及混沌现象的奇异和复杂性尚未为人们所彻底理解，人们一直认为混沌系统不能被人为地控制和诱导，在实际中混沌是有害的，因而总是尽量避免混沌.但1990年美国马里兰州立大学的Ott，Grebogi和Yorke[1]三人提出了基于参数扰动的控制方法，第一次实现了混沌系统的控制，这才真正引起人们重视.随后，人们已经发现了大量的混沌控制方法，并将其应用到了实际的系统中.2009年Yang等人[2]提出了新的思想，即使附近没有预先存在的稳定流形，也可以稳定不稳定的混沌系统.这个方法的优越性在于，通过控制参数随时间变化的调整，稳定一个不稳定的方向，并且参数的调整还可以优化.2001年Bu等人[3]提出了并不需要任何调节参数的控制方法，并得到了广泛的应用[4].在诸多学者成果[5-8]的基础上，本文采用这一个新的、更有效的控制方法，将三维离散的Hénon-like系统[9]稳定到固定点处，最后给出了数值模拟的结果.

考虑n维动力系统

其中x∈Rn是n维向量，F是非线性向量函数.设xf是映射（1）的固定点.为了将混沌系统稳定在这一固定点处，构造如下变量反馈控制：

定义xk在xf的无穷小偏差δxk=xk-xf.利用系统（2）可得到

将方程（4）代入方程（3）消去δxk，并选择Q=qI,q∈(-1,1)这一特殊形式，可得

利用这一方法，我们接下来将三维离散的Hénon-like系统[9]稳定到固定点处.

2 控制三维离散Hénon-like混沌系统

考虑离散的Hénon-like系统

其中α,β是参数.

不难求得系统有4个固定点：(-0.3994045033,0.9708330748,-0.07988090067), (0.6064282855,0.6064282855,0.1212856571),(0.9708330748,-0.3994045033,0.1941666150)，和(-1.177856857,-1.177856857,-0.2355713714).我们选择第一个作为研究对象.接下来，利用上述方法，我们将不稳定的离散系统稳定在这一固定点处.在固定点(y1f,y2f,y3f)处Jacobian矩阵为

从方程（5）可得

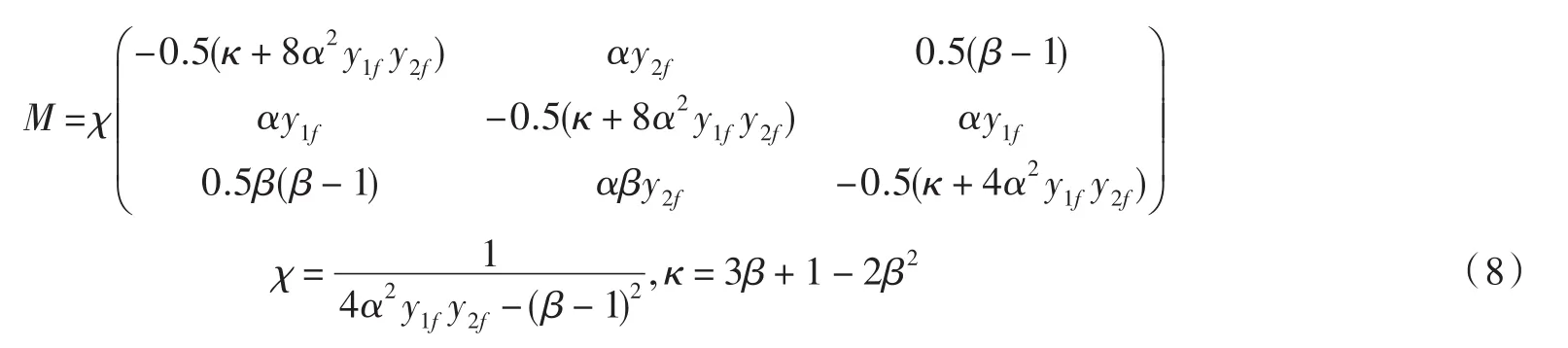
其中(y1f,y2f,y3f)=(-0.3994045033,0.9708330748,-0.07988090067),α=1.4,β=0.2.分别取q=0.5,q=-0.5，相应得

根据方程（2），将（9）代入到（6）可得：

3 数值模拟控制结果

首先我们给出控制前系统的轨迹图形，如图1所示.

通过新的控制方法，我们将系统的状态变量(y1(k),y2(k),y3(k))稳定在点(-0.3994045033,0.9708330748, -0.07988090067).下面将控制前后的轨迹图形比较如下，如图2、图3、图4所示.

最后，通过取不同的初始值，数值模拟出系统（10）的控制效果，如图5所示.

图1 Henon-like系统轨迹

图2 控制前后y1(k)随时间的轨迹图

图3 控制前后y2(k)随时间的轨迹图

图4 （a）控制前后y3(k)随时间的轨迹图

从数值模拟图5的结果不难发现，Henon-like系统的状态变量(y1(k),y2(k),y3(k))迅速地稳定在点(-0.3994045033,0.9708330748,-0.07988090067).

4 总结

利用新的控制方法，三维离散超混沌He⁃non-like系统被稳定在固定点处.通过控制稳定的过程，充分体现了这一控制方法既不需要对系统进行任何先验分析，也不需要事前调节任何控制参数.数值模拟结果充分证明了控制方法的有效性.

图5 控制后Henon-like系统轨迹

[1]Edward Ott,Celso Grebogi,James A.Controlling chaos[J].Phys Rev Lett,1990,64:1196-1119.

[2]Yang Ling,Liu Zengrong,Mao Jianmin.Controlling Hyperchaos[J].Phys Rev Lett,2000,84:67-70.

[3]Bu Shouliang,Wang Shaoqing,Ye Hengqiang.Stabilizing unstable discrete systems[J].Phys Rev E,2001,64:046209.

[4]Li Xin,Chen Yong.Stabilizing of Two-Dimensional Discrete Lorenz Chaotic System and Three-Dimensional Discrete Rrossler Hyperchaotic System[J].Chin Phys Lett,2009,26:090503.

[5]Yan Zhenya.Chaos Q-S synchronization between Rössler system and the new unified chaotic system[J].Phys Lett A,2005,334: 406-412.

[6]Chen Yong,Li Xin.Function Projective Synchronization between two identical chaotic Systems[J].International Journal of Modern Physics C,2007,18(5):883-888.

[7]Lü Jinhu,Chen Guanrong,Chen Daizhan.A new chaotic system and beyond:the generalized Lorenz-like system[J].Int J Bifur Chaos,2004,12:1507-1537.

[8]Li Xin,Chen Yong,Li Zhibin.Function Projective Synchronization of Discrete-Time Chaotic Systems[J].Z Naturforsch,2008,63a: 7-14.

[9]Yan Zhenya.Q-S(complete or anticipated)synchronization backstepping scheme in a class of discrete-time chaotic(hyperchaotic) systems:A symbolic-numeric computation approach[J].Chaos,2006,16:013119.

Controlling Unstable Discrete Chaotic System

LI Xin,QIAN Su-ping
(School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China)

Recently,a new control method has been constructed,which does not need any adjustable parame⁃ters.Using this new discovery,three-dimensional discrete Henon-like system is researched to be stabled at the fixed point.Finally,the controlling.effectiveness of the numerical simulations is given.

Discrete Henon-like system;chaos control;feedback control

O175

A

1008-2794（2013）04-0005-04

2013-04-26

国家自然科学专项基金“若干非线性耦合系统的对称性和敏感性研究”（11141003）

钱素平，教授，博士，研究方向：非线性方程，E-mail：qsp@cslg.edu.cn.