关于自然光在两种介质分界面上反射和折射时的偏振特性讨论

郭中华

（兰州城市学院培黎工程技术学院，甘肃 兰州 730070）

在一些基础光学教材［1，2］中，讨论光在两种介质分界面上发生反射、折射现象时光的偏振态变化规律时，主要侧重于利用菲涅尔公式分析光矢量振幅的变化规律，对于反射光和折射光的偏振度，只作简单的介绍.文献［3］中利用入射、折射时的光强关系，详细讨论了自然光在介质分界面上折射时的偏振度，并建立了实验系统进行验证，实验表明，折射光偏振度随入射角的增大而单调增加，布儒斯特角对其没有影响，并不像基础光学教材中认为的那样.另有文献［4］定量分析了反射光和折射光偏振度与布儒斯特角的关系，以n＝1.56的玻璃介质为例，得到与文献［3］不同的结果，肯定了有关教科书的结论.本文从理论上详细分析了自然光在分界面上反射光和折射光的偏振特性，并进一步探讨了偏振度变化的规律及与介质折射率、光强反射率、透射率和介质层数的关系.

1 反射光和折射光的偏振度

设折射率为n2的均匀介质Ⅱ处于折射率为n1的介质Ⅰ中，自然光以入射角i1入射到上表面，发生两次反、折射从下表面出射，取N（＝1）为介质层数.在介质上表面发生反、折射时，入射光、反射光和折射光振幅中各分量的比例关系可由菲涅尔公式［5］给出

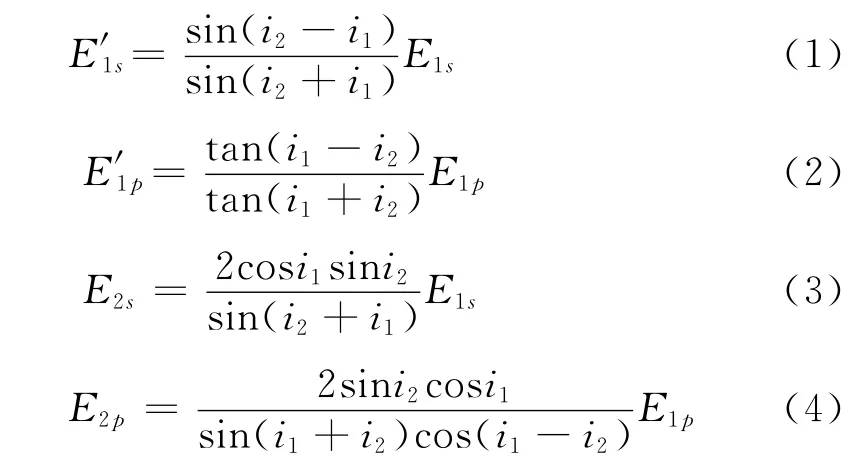
图1 自然光在介质分界面上的反射、折射情况

为了得到反射光和折射光的偏振度，根据不同介质中光强的定义

则相应入射光的光强为

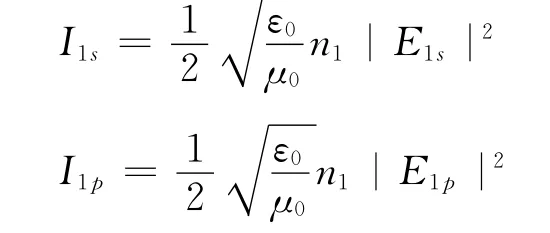
反射光的光强为

入射光为自然光，有｜E1s｜＝｜E1p｜，由于入射光和反射光在同种介质中，因此光强反射率为

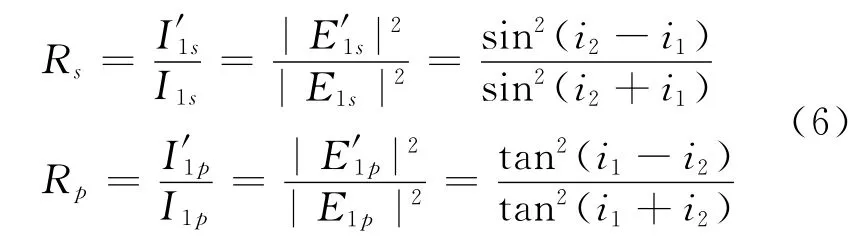
根据偏振度的定义［1］，则反射光的偏振度为

同理可知折射光的光强为

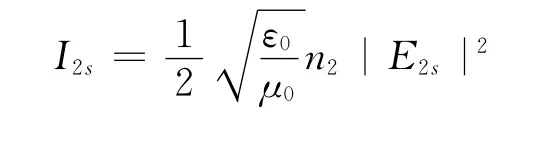
折射光和入射光在不同介质中，因此光强透射率为

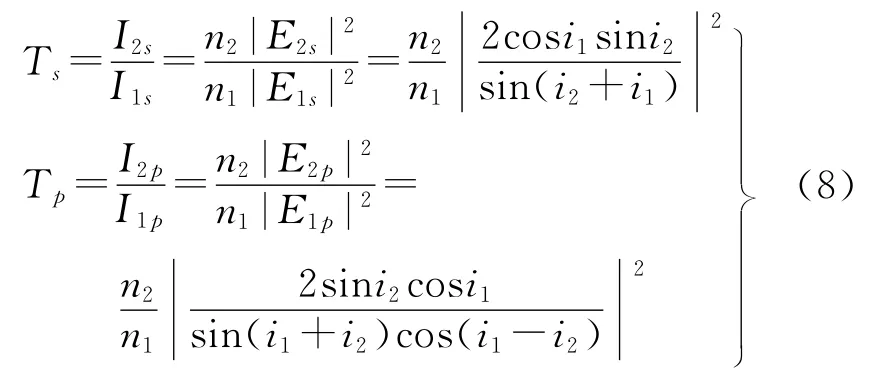
可知折射光的偏振度为

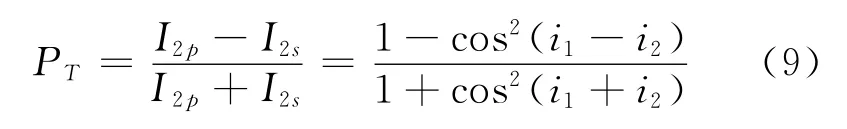
当自然光以任意入射角i1入射，由式（7）和式（9）可知0＜P＜1，反射光和折射光均为部分偏振光.

2 反射光和折射光偏振度的变化规律

2.1 不同介质分界面处反射光和折射光偏振度随入射角的变化

如图1情形，首先考虑自然光在介质上表面反射、折射时的偏振度变化规律.为了讨论简便，取介质Ⅰ为空气，介质Ⅱ为玻璃，折射率n2范围在1.5～1.8，根据式（7）结果，可得到在不同入射角下反射光偏振度随折射率的变化曲线（图2）及随入射角的变化曲线（图3）.可以看到，不同介质表面反射光的偏振度变化特征类似，先随入射角的增大而增加，取得极值（PR＝1）后随入射角的增大而减小，随着介质折射率的增加，偏振度极值位置向角度增大的方向移动.

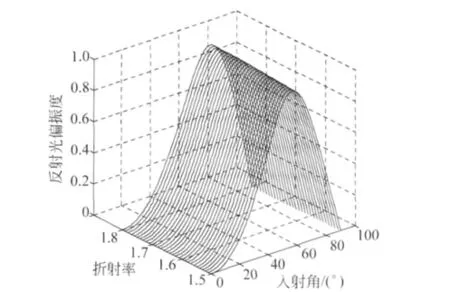
图2 不同入射角下反射光偏振度随折射率的变化

根据式（6）可得到光强反射率随入射角的变化曲线（图4），可以看出反射光中s分量的相对强度随入射角单调增加，而p 分量的相对强度先随入射角减小，因此反射光偏振度在这一过程中逐渐增大，随着p 分量的相对强度在布儒斯特角（i0＝arctan（n2/n1））处降为零，此时反射光中只有s分量，从而偏振度最高，而后随着入射角的增加p 分量的强度迅速增大，所以反射光偏振度又逐渐减小.

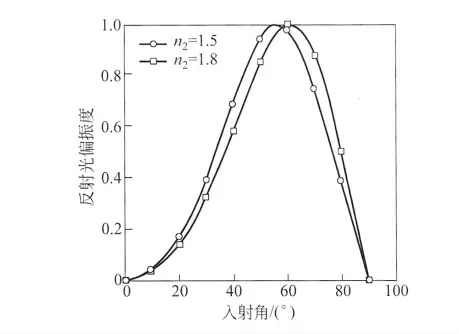
图3 反射光偏振度随入射角的变化

图4 光强反射率随入射角的变化

对于折射光而言，由式（9）结果，亦可得到在不同入射角下折射光偏振度随折射率的变化曲线（图5）及随入射角的变化曲线（图6）.

可以看出，在介质折射率n2＝1.5～1.8范围内，折射光偏振度的变化特征是类似的，均随着入射角的增大而单调增加，没有特例，这与文献［3］的结果是一致的，并不像基础光学教材中所描述“以布儒斯特角入射时，折射光的偏振度最高”［1，2］.

根据式（8）可得到光强透射率随入射角的变化曲线（图7），可以看出，s分量和p 分量相对强度均是随着入射角单调减小的，尽管在布儒斯特角处p 分量100%透射，透射光能流在此处取得最大值，但对于偏振度定义公式（9）来说相对强度的比例关系使得偏振度的变化不受这一特殊角度的影响.

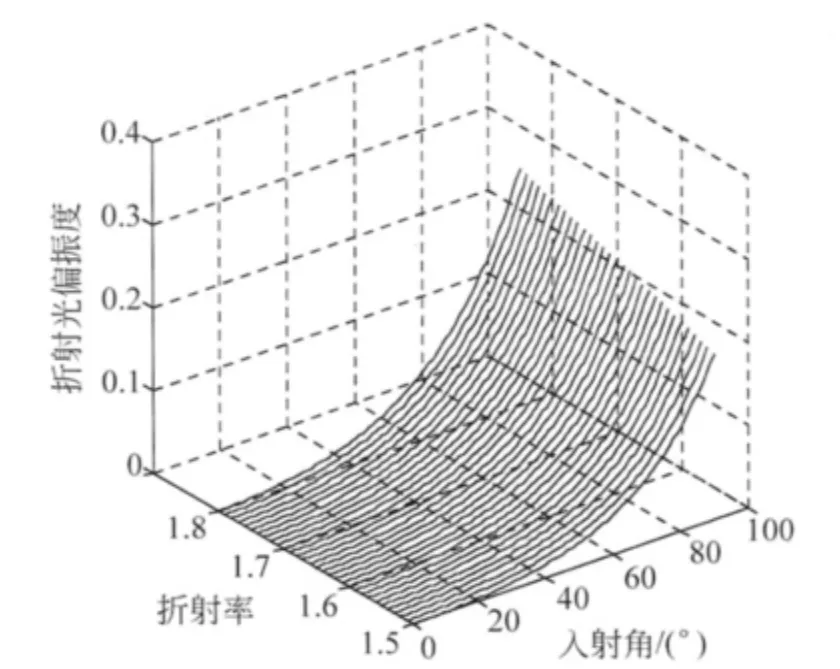
图5 不同入射角时折射光偏振度随折射率的变化

图6 折射光偏振度随入射角的变化

图7 光强透射率随入射角的变化

2.2 透射光偏振度随介质层数的变化

在图1情形中，当折射光经介质下表面透射出时，由式（3）和式（4）的结果可知透射光各分量振幅关系为

因此透射光的偏振度为

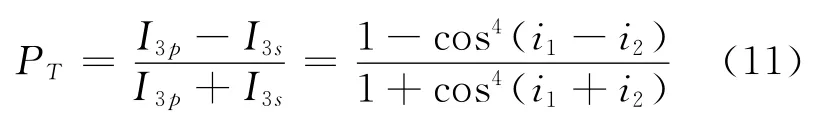
由此可得到经过单层介质透射后，不同入射角下透射光偏振度随折射率的变化曲线（图8）及随入射角的变化曲线（图9），所得结果和图5中类似，不同介质材料的透射光偏振度均随入射角增加而单调增大，没有特例，经过单层介质后，透射光的偏振度数值均明显增大.

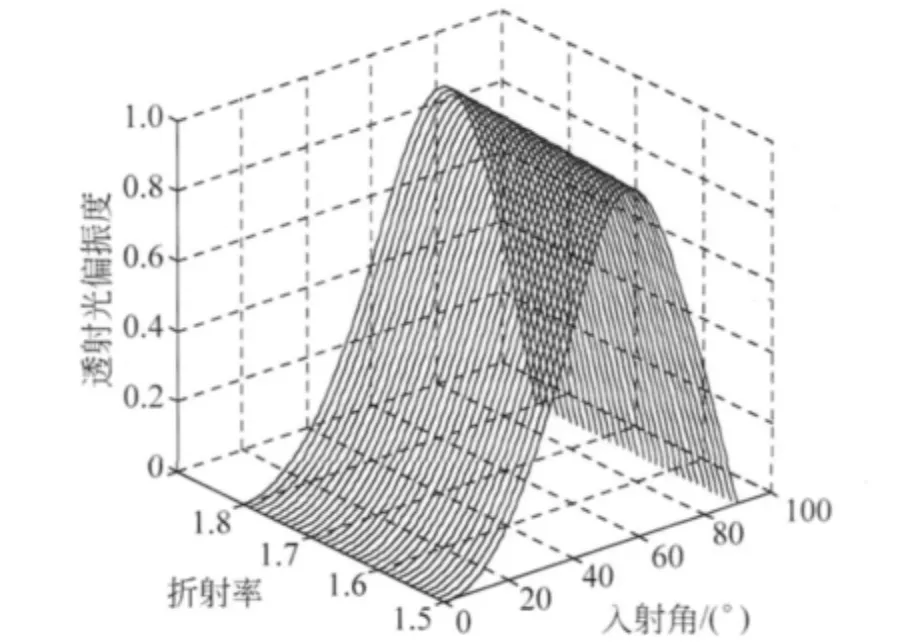
图8 N=1时不同入射角下透射光偏振度随折射率的变化

图9 N=1时透射光偏振度随入射角的变化

从式（11）可推知经由N 层平行介质层后，透射光的偏振度为

介质层数目对偏振度的影响如图10所示，随着介质层数目的增多，透射光的偏振化程度明显加快，在小角度情况下迅速达到1变成全偏振光.

3 结论

本文详细分析了自然光从空气到各种玻璃介质反射光和折射光的偏振特性，分析结果具有一般性，结果表明：

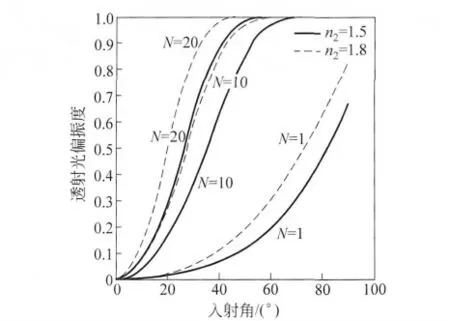
图10 透射光偏振度随介质层数的变化

（1）当自然光入射角0＜i1＜i0时，反射光偏振度随入射角单调增大，在相同入射角情形下，折射率越大的介质表面，反射光偏振度越小；在i1＝i0时反射光偏振化程度最大PR＝1，反射光为全偏振光；当i0＜i1＜90°时，反射光偏振度又随入射角增大而单调变小，相同入射角情形下，折射率越大的介质表面，反射光偏振度越大.

（2）不同介质材料透射光的偏振度变化规律类似，均随入射角的增大而单调增大，与是否以布儒斯特角入射无关，在折射率范围n2＝1.5～1.8内没有特例，在相同入射角情形下，折射率越大的介质材料其透射光偏振度也越大.

（3）介质层数目越多，相同入射角下透射光偏振度越大，对折射率n2＝1.5的介质，介质层数目在17层透射光可变为全偏振光，而对折射率n2＝1.8的介质，介质层数目在10层透射光就变为全偏振光.

［1］姚启钧.光学教程［M］.4版.北京：高等教育出版社，2008：215－222.

［2］廖延彪.偏振光学［M］.北京：科学出版社，2003：28－30.

［3］王静，宋连科，刘云安，等.自然光在多层介质分界面上折射时的偏振度［J］.大学物理，2006，25（4）：36－38.

［4］高润梅.自然光在两种介质表面发生反射和折射时的偏振特性［J］.兰州大学学报：自然科学版，2008.44（专辑）：292－294.

［5］赵凯华，钟锡华.光学［M］.北京：北京大学出版社，1984：245－260.