高斯-谢尔模型光束通过聚焦光学系统的偏振特性
2014-06-23朱东旭焦宏伟
陈 凯,朱东旭,焦宏伟
高斯-谢尔模型光束通过聚焦光学系统的偏振特性
陈 凯,朱东旭,焦宏伟
(中国卫星海上测控部,江阴214431)
为了研究高斯-谢尔模型光束的偏振特性,采用交叉谱密度矩阵的方法,研究了该光束通过聚焦光学系统的偏振特性,得到了完全偏振和完全非偏振光束保持偏振度不变的条件,并给出了通过聚焦光学系统后传输平面偏振度实现均匀分布的条件。结果表明,聚焦光学系统中偏振度在焦点位置附近有明显的起伏变化;焦点位置上的偏振度等于其在自由空间传输时的远场稳定偏振度。该研究对激光传输领域具有重要的理论和现实意义。
激光光学;偏振特性;交叉谱密度矩阵;高斯-谢尔模型光束;聚焦光学系统
引 言
1 理论模型
假设随机电磁光束沿着z轴的正方向传输,并以ABCD光学系统为传输路径,如图1所示。

Fig.1 Illustration of stochastic electromagnetic beams through an ABCD optical system
随机电磁光束的统计特性可以由2×2交叉谱密度矩阵来描述[9]:

式中,ρ1和ρ2为光束中的任意两点,x和y分别为电场矢量E相互垂直的两个偏振方向,*表示复共轭,〈〉表示系综平均。
根据柯林斯公式[10],光电场通过ABCD光学系统的传输公式为:

式中,S1是光源处面积,L表示的是输入平面和输出平面之间的程函:L(ρ,ρ′,z)=z+(Aρ2+Dρ′2-2ρ·ρ′)。根据(1)式,可以得到交叉谱密度矩阵元经过ABCD光学系统的传输公式[11-12]:

其中,

式中,ax,bx,cx,dx为x-O-z平面内的传输矩阵元,ay,by,cy,dy为y-O-z平面内的传输矩阵元[11]。对于不同的ABCD系统,其传输矩阵元的取值是不同的。当光学系统为轴向对称时,满足关系[11]:ax=ay,bx=by,cx=cy,dx=dy。
计量资料利用SPSS19.0软件分析并经t检验(均数±标准差),计数资料经X2检验(率)。存在统计学意义评定标准:P<0.05。
目前研究较多的随机电磁光束是所谓的高斯-谢尔模型光束,其强度分布和空间相干度都是高斯函数[13]。为了便于计算和分析,这里以高斯-谢尔模型光束为研究对象。设光源上任意一点的光谱强度的i分量为Si(ρ′,ω),任意两点电场矢量的i分量与j分量的相关度为uij(ρ2′-ρ1′,ω),其相关表达式如下所示[14]:

式中,Ai表示光场i分量的振幅,σi表示光斑i方向的大小,Bij表示光场i分量和j分量的相关系数,δij表示相关长度[14]。参量Ai,σi,Bij和δij均与位置无关,只取决于频率ω[14]。这些参量并不是任意取的,需要满足以下条件[15]:
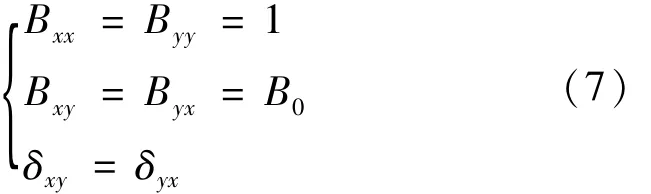
于是,光源处的交叉谱密度矩阵元有如下形式[15]:

为了方便积分,这里需要进行坐标系转换,将极坐标转换成直角坐标:ρ1=(x1,y1)T,ρ2=(x2,y2)T,ρ1′=(x1′,y1′)T,ρ2′=(x2′,y2′)T。将(5)式、(6)式和(8)式代入(3)式进行积分计算,可求得高斯-谢尔模型光束经过ABCD光学系统的交叉谱密度矩阵元:
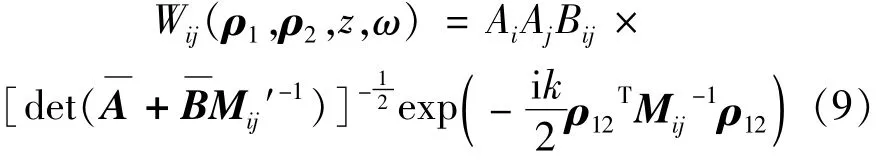


根据偏振度的定义[16],不难得到传输空间任意一点的偏振度P(ρ,z,ω):式中,tr,det分别表示交叉谱密度矩阵的迹和秩。引入聚焦光学系统的传输矩阵条件,即可得到高斯-谢尔模型光束在该条件下的交叉谱密度矩阵,从而可实现对观察点偏振特性的研究。
2 数值计算
根据(9)式和(11)式,具体研究高斯-谢尔模型光束通过聚焦光学系统的偏振特性,其相应传输矩阵元取值为[17]:ax=ay=1-z/f,bx=by=z,cx=cy=-1/f,dx=dy=1。在数值模拟中,采用研究较少的各向异性光束,即光束起始面内偏振度分布不均匀(σx≠σy)的情况。光束参量设置如下:λ=632.8nm,Ax=1,Ay=3,B0=0.3,σx=1cm,σy=3cm,δxx=1mm,δyy=3mm,δxy=2mm,聚焦光学系统的焦距f=1m。
图2中分别选择了不同的Ay/Ax,B0,δyy/δxx,δxy,σy/σx和f反映轴上偏振度随传输距离的变化关系。通过数值模拟计算表明,对于聚焦光学系统传输,轴上偏振度的变化趋势与光束参量的选择有关,其在焦点附近有明显的起伏变化,继续传输一段距离后该偏振度恢复其未到达焦点附近时的大小,这与已有的结论[18]一致。

Fig.2 The variation of the polarization degree on the axeswith the distance for different parameterswhenρ=0
现针对上述结论[18]给出解析证明。根据聚焦光学系统的条件和(9)式,可得到焦点处的交叉谱密度矩阵元:

将(12)式代入(11)式,得到焦点处的光谱偏振度:

式中,q1,q2和q3为代换后的参量:

同样,根据自由空间的条件[12](ax=ay=1,bx=by=z,cx=cy=0,dx=dy=1),将(8)式代入(11)式,并对传输距离z取无穷远的极限,可得到该稳定偏振度的表达式:
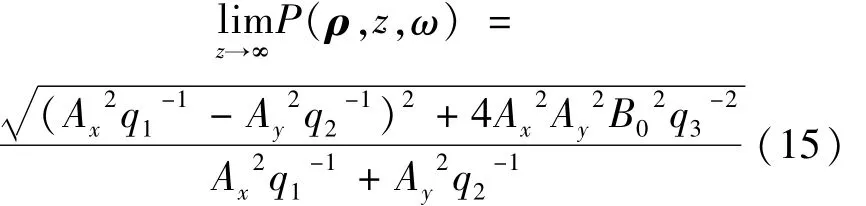
比较(13)式与(15)式,发现两者完全相等。由此可以得出结论,聚焦光学系统中焦点处的偏振度与光源参量的选择有关,其值等于自由空间条件下远场的偏振度稳定值。所以,利用聚焦光学系统可以在较短的距离内测得自由空间传输时的稳定偏振度。
接下来研究完全偏振光束和完全非偏振光束这两种特殊的情况。对于完全偏振光束,即B0=1,δxx=δyy=δxy=1mm;而对于完全非偏振光束,即Ax=Ay=1,B0=0,σx=σy=1cm。
由图3a可以看出,当σx=σy时,完全偏振光的偏振度传输不变;当σx≠σy时,完全偏振光束在焦点附近变为部分偏振,在远场又趋于完全偏振。这说明,光谱密度特性对传输中的偏振度产生影响,其保持完全偏振状态的条件是σx=σy。由图3b可以看出,当δxx=δyy时,偏振度在传输中不会发生变化,光束保持完全非偏振的状态;当δxx≠δyy时,光谱偏振度在焦点附近会发生变化,由完全非偏振变为部分偏振,但在远场又趋于完全非偏振。这说明,光束相干性影响了传输中的偏振度,其保持完全非偏振状态的条件是δxx=δyy。
图4中给出了不同传输平面内偏振度的分布关系。不难看出,当z=0.5m时,传输平面上各点的偏振度相等。
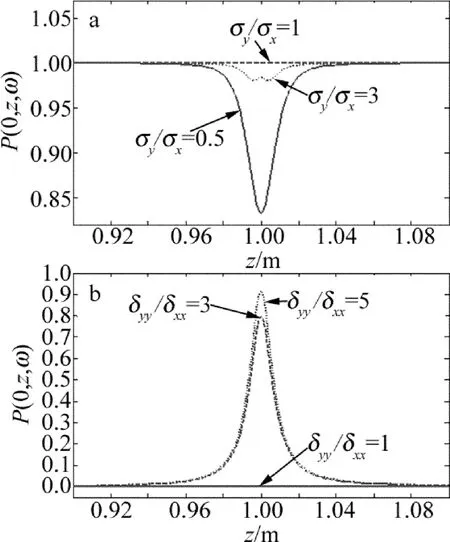
Fig.3 The variation of the polarization degree on the axes with distance whenρ=0,f=1m

Fig.4 The distributuion of the polarization degree at different transmission plane when f=1m
对该现象可从解析上进行解释。将(9)式代入(11)式,经化简并提取公因式发现,要实现传输平面上偏振度均匀分布,必须满足条件:

将聚焦光学系统的传输矩阵元代入(16)式,得到了聚焦光学系统的传输平面上实现偏振度均匀分布的条件为:

将该条件代入(11)式计算,得到z=f/2传输平面上的偏振度:

式中,q4也为代换后的参量:

不难看出,该偏振度与位置ρ无关。在聚焦光学系统中实现传输平面上偏振度均匀分布的条件为z=f/2,这一点在以往的研究中未有提及。
3 结 论
为研究高斯-谢尔模型光束通过聚焦光学系统的偏振特性,推导得到了该条件下的交叉谱密度矩阵。研究发现,对于聚焦光学系统,轴上偏振度在焦点附近有明显的起伏变化;位于焦点位置上的偏振度等于其在自由空间传输时的稳定偏振度,利用此结论可以在较短的距离内测得自由空间传输时的远场稳定偏振度;σx=σy和δxx=δyy分别是完全偏振和完全非偏振高斯-谢尔模型光束在聚焦光学系统中保持偏振度不变的条件;在z=f/2的传输平面内偏振度实现均匀分布。
[1] WOLF E.Unified theory of coherence and polarization of random electromagnetic beams[J].Physics Letters,2003,A312(5):263-267.
[2] SALEM M,KOROTKOVA O,DOGARIU A,et al.Polarization changes in partially coherent electromagnetic beams propagating through turbulent atmosphere[J].Waves Random Media,2004,14(4):513-523.
[3] JIX L,ZHANG E T,LÜB D.Changes in the spectrum and polarization of polychromatic partially coherentelectromagnetic beams in the turbulent atmosphere[J].Optics Communications,2007,275(2):292-300.
[4] JIX L,CHEN S H,LIX Q.Polarization properties of partiallycoherent electromagnetic Hermite-Gaussian beams in atmospheric turbulence[J].Chinese Journal of Lasers,2008,35(1):67-72(in Chinese).
[5] EYYUBOGLU H T,BAYKAL Y,CAIY.Degree of polarization for partially coherent general beams in turbulent atmosphere[J].Applied Physics,2007,B89(1):91-97.
[6] JAMESD F V.Change of polarization of light beams on propagation in free space[J].Journal of the Optical Society of America,1994,A11(5):1641-1643.
[7] KOROTKOVA O,WOLFE.Changes in the state of polarization of a random electromagnetic beam on propagation[J].Optics Communications,2005,246(1):35-43.
[8] SHIRAIT.Polarization properties of a class of electromagnetic Gaussian Schell-model beamswhich have the same far-zone intensity distribution as a fully coherent laser beam[J].Optics Communications,2005,256(4):197-209.
[9] WOLF E.Correlation-induced changes in the degree of polarization,the degree of coherence,and the spectrum of random electromagnetic beams on propagation[J].Optics Letters,2003,28(13):1078-1080.
[10] LÜB D.Laser optics[M].Chengdu:Sichuan University Press,1992:191-231(in Chinese).
[11] ZHAO D M,ZHU Y B.Generalized formulas for stochastic electromagnetic beams on inverse propagation through nonsymmetrical optical systems[J].Optics Letters,2009,34(7):884-886.
[12] ZHANGGW,PU JX.Stochastic electromagnetic beams focused by a bifocal lens[J].Journal of the Optical Society of America,2008,A25(7):1710-1715.
[13] KOROTKOVA O,SALEM M,WOLF E.Beam conditions for radiation generated by an electromagnetic Gaussian Schell-model source[J].Optics Letters,2004,29(11):1173-1175.
[14] GORIF,SANTARSIERO M,PIQUERO G,et al.Partially polarized Gaussian Schell-model beams[J].Journal of Optics,2001,A3(1):1-9.
[15] ROYCHOWDHURY H,KORPTLPVA O.Realizability conditions for electromagnetic Gaussian Schell-model sources[J].Optics Communications,2005,249(4):379-385.
[16] JI JR.Advanced optics tutorial[M].Beijing:Science Press,2007:261-267(in Chinese).
[17] DU X Y,ZHAO D M,KOROTKOVA O.Cross-spectral density matrix of a random electromagnetic beam propagating through an apertured axially nonsymmetrical optical system[J].Physics Letters,2008,A372(22):4135-4140.
[18] DU X Y.Studies on the propagation and scattering of the vector or scalar light beams through the complicated optical systems and media[D].Hangzhou:Zhejiang University,2010:24,43-48,73-85(in Chinese).
Polarization properties of Gaussian-Schellmodel beam s passing through focal optical system
CHENKai,ZHUDongxu,JIAOHongwei
(China Department of Satellite Marine Tracking and Control,Jiangyin 214431,China)
In order to study polarization properties of Gaussian-Schell model beams,the method of cross-spectral densitymatrix was adopted to study polarization properties of Gaussian-Schell model beams propagating through a focal optical system.The conditions,under which complete polarized and complete non-polarized beams kept the degree of polarization invariable in the focal optical system,were provided.The condition where the degree of polarization distributed homogeneously at propagation plane was also given.The degree of polarization had a sharp fluctuation at focal position in a focal optical system.The degree of polarization at focal position equaled the stable value of the degree of polarization at far field.The study had important theoretical and practical significance in the field of laser transmission.
laser optics;polarization properties;cross-spectral density matrix;Gaussian-Schellmodel beam;focal optical system
O436.3
A
10.7510/jgjs.issn.1001-3806.2014.02.021
1001-3806(2014)02-0246-05
陈 凯(1986-),男,硕士,助理工程师,现从事高能激光技术等方面的研究。
E-mail:629167307@qq.com
2013-04-24;
2013-06-03
