压力型锚杆锚固段长度确定方法研究

廖 军，涂兵雄

（1.西南交通大学 土木工程学院，成都610031；

2.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连116024）

随着经济建设的发展和科学技术的进步，岩土锚固技术已在边坡、基坑、矿井、隧洞、地下工程、水坝等工程建设中得到了广泛的应用［1－5］。而在岩土锚固技术中，锚固段长度的计算是至关重要的一个环节。规范［6］规定：对于土层锚杆，锚固段长度不应小于4m，且不宜大于10m；对于岩石锚杆，锚固段长度不应小于3，且不宜大于6.5m或8m（对预应力锚索）。文献［7－12］的研究都表明，锚杆的承载力并不随锚固段长度的增加而一直增长，超过一定的长度后，超出的锚固段长度几乎不起作用。张洁等［13］通过理论分析和研究得出了锚杆临界锚固段长度的求解公式，但需要通过现场拉拔试验的P－S关系反演获得锚杆的侧摩阻刚度系数，或者需要监测出锚杆锚固段后1／3点处的轴力，这给锚杆的前期设计工作带来一定的困难，使用起来不是很方便。且该公式仅限用于拉力型锚杆。

而目前，由于压力型锚杆具有较好的受力性能和防腐特性，在实际工程中尤其是永久性工程中被广泛使用［1－3，9，11］，但 有 关 压 力 型 锚 杆 锚 固 段 长 度 计算方法的研究成果相对较少。曹兴松等［14］采用Winkler假设，基于锚索粘结应力分布的特点，通过锚索锚固段受力状态分析和应力分布规律，利用理论与试验结果相对比，提出了一种新的设计方法，但引入了综合切向刚度系数，且确定该系数存在一定的困难，使用不便。规范［6］假定锚固段上的侧摩阻力均匀分布，据此设计锚固段长度，虽计算简便，但又与锚固段侧摩阻力非线性分布的客观事实不符。因此，故本文在文献［15］和［16］研究成果的基础上，考虑锚固体与岩土体间的粘结力，引入岩土体粘聚力工作条件系数，对压力型锚杆锚固段长度的计算方法进行了一定的研究和分析。

1 理论推导

1.1 基本假设

以压力型锚杆底部的承载体为坐标原点建立一维直角坐标系，如图1所示。

图1 压力型锚杆坐标示意图

为方便计算分析，假定锚固层的荷载传递模型为理想的弹塑性模型［17］，承载体截面处的剪应力达到极限侧摩阻力时，锚杆达到极限承载力，锚杆在达到极限承载力之前，锚固层处于弹性工作状态［13］；锚固体与岩土体交界面上满足库仑准则；锚固体截面上的轴向应力均匀分布。

1.2 公式推导

沿锚固体轴线方向取一微段进行受力分析，如图2所示。由微元体的水平方向平衡可得：

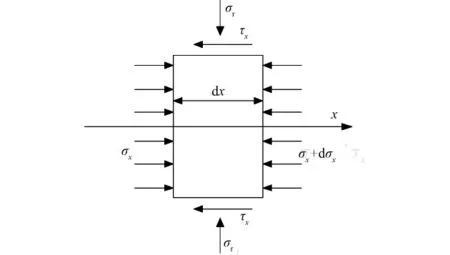
图2 锚固段微元体受力图

式中：R为锚固体半径；σx为锚固体截面上的正应力；τx为锚固体与岩土体交界面上的剪应力。

考虑锚固体与岩土体交界面摩擦角的影响，建立图3所示的莫尔圆坐标系，则锚固体与岩土体交界面上剪应力为：

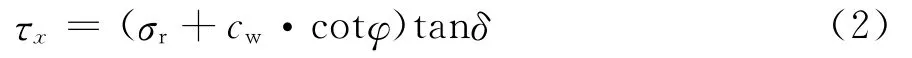
式中：σr为锚固体与岩土体交界面上的正应力；cw为锚固体与岩土体间的粘结力；φ为岩土体内摩擦角；δ为锚固体与岩土体交界面上的外摩擦角，由于压力型锚杆的锚固体受压，会对周围岩土体产生径向的挤压效应（不同于拉力型锚杆），锚固体和岩土体界面上的外摩擦角可能大于岩土体内摩擦角。考虑到实际锚固体与岩土体间粘结力和岩土体粘聚力的差异，取cw＝ξ·c，ξ为岩土体粘聚力工作条件系数，取0.7～1.0［4］，c为岩土体粘聚力。

图3 锚固体与岩土体交界面上的应力莫尔圆

由弹性力学空间问题柱坐标下的物理方程［17］有：

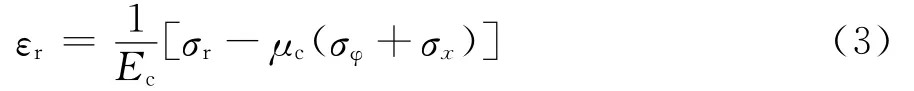
式中：εr为锚固体径向应变；Ec为锚固体弹性模量；μc为锚固体泊松比；σφ为锚固体截面的环向应力。

根据前面的假设有σφ＝σr，代入式（3）有：

由弹性力学［17］解答可得半径为R的圆孔受均布内压力σr时任一点的径向位移：

式中：ur为锚固体径向位移；μs为岩土体泊松比；Es为岩土体弹性模量；r为岩土体上任一点到圆孔圆心的距离。

在锚固体与土体交界面上，即r＝R处，根据变形协调，由式（4）和式（5）得：

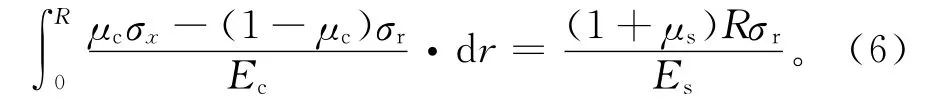
整理得：

将式（7）和式（2）代入式（1）有：

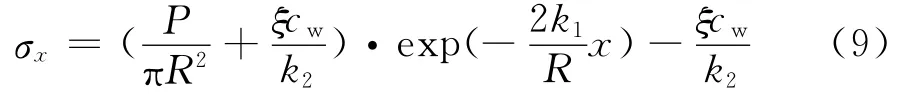
联立式（2）、（7）、（9）可得锚固体与岩土体界面上任一点的剪力：

由式（9）得锚固体内任一点x处的轴压力：

式（10）、（11）即为锚固段的剪力和轴力分布公式，式中完整地包含了岩土体粘聚力、内摩擦角、弹性模量和泊松比；锚固体的弹性模量、泊松比、半径以及与岩土体交界面外摩擦角；外荷载对锚固体上剪应力和轴力分布的影响。

1.3 锚固段长度计算

承载体截面处剪应力达到极限侧摩阻力之前，实际发挥作用的锚固段长度随外荷载的增加而增加，锚固体与岩土体界面上相应的剪力也不断增加，并逐渐向更深处传递。从式（11）可以看出，压力型预应力锚杆中锚固体内任一点x处的轴压力随锚固体长度的增加呈指数衰减，直至为0，轴力零点与承载体间的锚固段长度为实际发挥作用的锚固段长度，也就是锚固段上荷载的传递长度。令式（11）等于零，得：

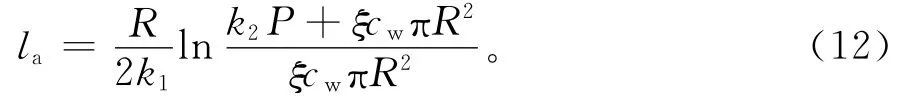
对于即定的锚杆体系，其极限承载力是诸多结构极限承载力的综合反映，锚杆体系的极限承载力取决于这些极限承载力中的最小值。如果需要提高锚杆体系的极限承载力，就需要保证体系中极限承载力最小的结构满足设计要求即可。

锚杆体系的极限承载力由以下极限承载力综合决定：锚下承载结构极限承载力Pu1、锚下岩土体极限承载力Pu2、锚杆杆体的极限承载力Pu3、锚固体的极限抗压承载力Pu4和锚固体极限侧阻力Pu5。其值取决于五者当中的最小值，即

则锚杆体系对应的锚固段长度为：

根据侧摩阻力非线性分布的假设，当按规范［4］计算得到锚固段长度大于式（14）计算得到的锚固段长度时，宜将压力型锚杆（集中型）设计成压力分散型锚杆，以降低锚固段侧摩阻力峰值，并使其充分发挥。

2 锚固段长度因素影响分析

为研究岩土体的弹性模量、泊松比、粘聚力、内摩擦角和外荷载对压力型锚杆中的锚固段长度的影响，选取典型的岩土体和锚固体参数对其进行分析，其中锚固体与岩土体界面外摩擦角取岩土体内摩擦角，具体参数见表1。在对其中一个参数进行分析时，其它参数保持不变。

表1 岩土体和锚固体参数

2.1 岩土体弹性模量的影响

图4是在不同的岩土体弹性模量下得到的锚固体的锚固段长度分布图。从图中可以清楚地看出，岩土体弹性模量越大，即岩土体越坚硬，则需要的锚固段长度越小。对一般土体而言，其弹性模量介于10～1 000MPa之间时，对应的锚固段长度介于10.5～7.5m之间；对一般岩体而言，其弹性模量介于1 000～6 000MPa之间时，对应的锚固段长度介于7.5～3.7m之间。

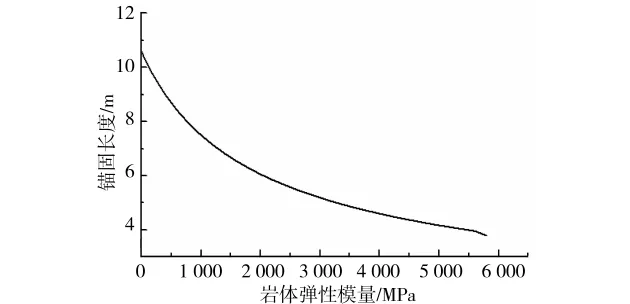
图4 不同岩土体弹性模量下的锚固段长度

2.2 岩土体泊松比的影响

图5 是在不同的岩土体泊松比下得到的锚固体的锚固段长度分布图。从图中可以清楚地看出，锚固体的锚固段长度随泊松比的增加而增加，且有明显的线性关系。但是泊松比从0.1增加到0.4时，锚固段长度仅从5.6m增加到6.1m，增幅仅约9%，可见岩土体泊松比对锚固段长度的影响很小，几乎可以忽略不计。因此，在用式（12）和（14）对压力型锚杆的锚固段长度进行估算和设计时，基本可以忽略岩土体泊松比变化对锚杆锚固段长度求解结果的影响。

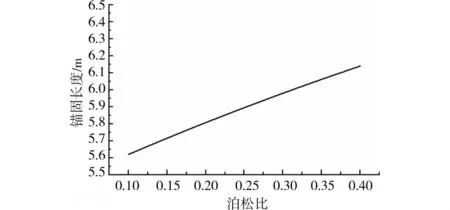
图5 不同岩土体泊松比下的锚固段长度

2.3 岩土体粘聚力的影响

图6 是在不同的岩土体粘聚力下得到的锚固体的锚固段长度分布图。从图中可以看出，岩土体粘聚力越大，锚固段长度越小。对于一般土体而言，其粘聚力介于10～40kPa之间时，对应的锚固段长度介于12.4～6.1m，且锚固段长度随粘聚力的增加急剧减小；对于一般岩体而言，其粘聚力大于40kPa时，锚固段长度小于6.1m，当粘聚力大于150kPa时，锚固段长度小于2.3m，且变化缓慢。

图6 不同岩土体粘聚力下的锚固段长度

2.4 岩土体内摩擦角的影响

图7 是在不同的岩土体内摩擦角下得到的锚固体的锚固段长度分布图。从图中可以看出，锚固段长度整体上随内摩擦角的增加而减小。对于一般土体而言，内摩擦角小于30°，锚固段长度介于5.0～10.2m之间；对于一般岩体而言，内摩擦角大于30°，锚固段长度小于5.0m。

2.5 外荷载的影响

图8是压力型锚杆在不同外荷载作用下得到的锚固体的锚固段长度分布图。从图中可以看出，当外荷载较小时，锚固体上荷载的传递范围较小，即实际发挥作用的锚固体长度较小；当外荷载增大时，锚固体上的荷载向更深处传递，即实际发挥作用的锚固体长度随荷载的增大而增加。从图中可以看出预应力从20kN增加到500kN时，锚固段长度从1.0m增加到10.0m。

图7 不同岩土体内摩擦角下的锚固段长度

图8 不同外荷载下的锚固段长度

3 实验验证

采用文献［18］在压力型锚杆试验中监测的试验数据与本文计算结果进行对比验证。该试验中M1锚杆的有关参数为模型尺寸：5m×0.8m×0.8m；锚索：2根1 860K级φ15.24高强度低松弛无粘结钢绞线（极限承载力518kN），锚具 OVM15－4型，φ95钢质承载体，φ20钢绞线孔，架线环每隔2m设置1个，预应力设计值200kN，预应力锁定值为220kN。锚固体和模拟软岩的有关参数如下表2所示。

表2 锚固体和岩土体参数

试验在张拉力为200、440kN作用下监测得到的荷载在锚固段中的传递长度分别为0.25、0.55m（都为监测点布置位置），考虑到实际监测的荷载传递长度（承载体至轴力零点的距离）只能是承载体至监测点的长度。

根据式（11）求得在不同张拉荷载下，锚固段上的轴力分布如图9所示。从图中可以看出，不同张拉荷载下，锚固段上的轴力分布很不均匀，荷载较大时，轴力衰减较快。采用本文推导公式计算得到试验锚杆在外荷载200、440kN时，对应的锚固段长度分别为0.31、0.51m。理论计算值和实测值比较吻合。

图9 不同张拉力下的轴力分布

另外，假定锚杆体系的极限承载力最终由锚索的极限承载力（518kN）控制，可求得该实验锚杆体系达到极限荷载时，对应所需的锚固段长度约为0.56m。

4 讨 论

考虑锚固体与岩土界面侧摩阻力的非线性分布，得到了计算锚固段长度的解析式，计算结果与试验结果吻合较好，说明本文计算方法正确可行。通过研究了不同岩土体参数下锚固段长度的变化范围，从图4～8可以看出，本文求解结果与规范建议的锚固段长度取值范围比较吻合，说明规范对锚固段长度的建议值是比较合理的。但是由于规范简单地假定锚固段侧摩阻力均匀分布，因此，当实际锚固段长度取值小于规范值时，对应的最大外荷载在锚固体与岩土界面产生的剪应力实际上要小于侧阻力极限值，结果偏安全；而当实际锚固段长度大于规范值时，在对应最大外荷载情况下，承载体处的侧阻力达极限时，由于在超出本文锚固段长度计算值或规范建议值以外的锚固段的实际侧阻力发挥作用很小，此时仍按规范的侧阻力均匀分布计算锚固段长度，有可能导致承载体在锚固段附件率先发生破坏并引发破坏长度进一步延伸，即渐进性破坏，使得锚固体总锚固力达不到设计要求，计算结果偏不安全，在实际工程中需引起注意。因此，当锚固段长度过长时，建议采取压力分散型锚索［15，18］，通过承载体作用来分担荷载，降低侧摩阻力峰值，充分发挥侧摩阻力强度，从而保证总锚固力满足设计要求。

5 结 语

1）推导出了压力型锚杆锚固段的剪应力和轴力计算公式，以及求解锚固段长度的解析式。式中的参数简便易得，计算方便，对压力型锚杆和压力分散型锚杆锚固段长度设计有很好的指导意义。

2）分析结果表明压力型锚杆的锚固段长度随岩土体弹性模量的增大而减小；随岩土体泊松比的增加成线性增长，但影响极为有限，几乎可以忽略不计；随岩土体粘聚力的增加而减小，且粘聚力小于40kPa时，减小较快，大于40kPa时，减小较慢；随内摩擦角的增大而减小；随外荷载（不超过锚杆体系的极限承载力时）的增大而增大。

3）不同岩土体弹性模量、泊松比、粘聚力、内摩擦角以及外荷载下得到的锚固段长度范围与规范的要求比较吻合。因此，考虑侧摩阻力的非线性分布规律，单个承载体对应的锚固段长度取值不宜大于规范建议值，取值过大会使侧摩阻力不能充分发挥，造成总锚固力偏不安全，实际工程中应引起注意。

4）本文提出的压力型锚杆的锚固段长度计算公式求解的结果与室内试验实测的荷载传递长度比较吻合。对压力型锚杆锚固长度的解答可为实际工程中锚固段长度的设计提供一定的参考。

［1］卢黎，张永兴，张四平，等.软质岩中压力型锚索锚固段应力分布特征［J］.土木建筑与环境工程，2011，33（5）：69－74.Lu L，Zhang Y X，Zhang S P.et al.Stress distribution in fixed anchor length of compression type anchor in soft rock mass ［J］.Journal of Civil，Architectural ＆Environmental Engineering，2011，33（5）：69－74.

［2］魏作安，朱彬，万玲，等.边坡锚固工程分析中的水平条分法［J］.土木建筑与环境工程，2010，32（3）：53－56.Wei Z A，Zhu B，Wan L，et al.Horizontal slice method for the stability analysis of reinforced slopes ［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2010，32（3）：53－56.

［3］卢黎，张永兴，吴曙光.压力型锚杆锚固段的应力分布规律研究［J］.岩土力学，2008，29（6）：1517－1520.Lu L，Zhang Y X，Wu S G.Distribution of stresses on bonded length of compression type rock bolt［J］.Rock and Soil Mechanics，2008，29（6）：1517－1520.

［4］贾金青，郑卫锋.预应力锚杆柔性支护法的研究与应用［J］.岩土工程学报，2005，11（27）：1257－1261.Jia J Q，Zheng W F.Study and application of flexible retaining method with prestressed anchor［J］.Chinese Journal of Geotechnical Engineering，2005，11（27）：1257－1261.

［5］程良奎.岩土锚固的现状与发展［J］.土木工程学报，2001，34（3）：7－12.Cheng L K.Present status and development of ground anchorages［J］.China Civil Engineering Journal，2001，34（3）：7－12.

［6］中华人民共和国建设部.GB 50330－2002建筑边坡工程技术规范［S］.北京：中国建筑工业出版社，2002.

［7］张乐文.岩土锚固理论研究之现状［J］.岩土力学，2002，23（5）：627－631.Zhang L W.Research on status of anchorage theory of rock and soil［J］.Rock and Soil Mechanics，2002，23（5）：627－631.

［8］Briaud J L，William F.David E.Weatherby，should grouted anchors have short tendon bond length ［J］.Journal of Geotechnical and Geoenvironmental Engineering，1998，124（2）：110－119.

［9］Kim N K.Performance of tension and compression anchors in weathered soil［J］.Journal of Geotechnical and Geoenvironmental Engineering，2003，129（12）：1138－1150.

［10］Barley A D.Discussion of“Performance of tension and compression anchors in weathered soil”［J］.Journal of Geotechnical and Geoenvironmental Engineering，2005：671－672.

［11］陈广峰，米海珠.黄土地层中锚杆受力性能试验分析［J］.甘肃工业大学学报，2003，29（1）：116－119.Chen G F，Mi H Z.Experimental analysis of anchor's stress performance in collapsible loess layer［J］.Journal of Gansu University of Technology，2003，29（1）：116－119.

［12］程良奎，胡建林.土层锚杆的几个力学问题［C］／／岩土工程中的锚固技术.北京：人民交通出版社，1996.

［13］张洁，尚岳全，叶彬.锚杆临界锚固长度解析计算［J］.岩石力学与工程学报，2005，24（7）：1134－1138.Zhang J，Shang Yu Q，Ye B.Analytical calculations of critical anchorage length of bolts［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（7）：1134－1138.

［14］曹兴松，周德培.压力分散型锚索锚固段的设计方法［J］.岩土工程学报，2005，27（9）：1033－1040.Cao X S，Zhou D P.Design method of fixed anchor unit for compression dispersion－type anchor ［J］.Chinese Journal of Geotechnical Engineering，2005，27（9）：1033－1040.

［15］贾金青，涂兵雄，王海涛，等.压力分散型预应力锚杆的力学机理研究［J］.岩土工程学报，2011，33（9）：1320－1325.Jia J Q，Tu B X，Wang H T.et al.Mechanical behaviors of pressure－dispersive prestressed anchor ［J］.Chinese Journal of Geotechnical Engineering，2011，33（9）：1320－1325.

［16］尤春安.压力型锚索锚固段的受力分析［J］.岩土工程学报，2004，26（6）：828－831.You C A.Mechanical analysis on anchorage segment of pressure－type cable［J］.Chinese Journal of Geotechnical Engineering，2004，26（6）：828－831.

［17］徐芝纶.弹性力学［M］.北京：高等教育出版社，2006.

［18］夏元友，陈泽松，顾金才，等.压力分散型锚索受力特点的室内足尺模型试验［J］.武汉理工大学学报，2010，32（3）：33－38.Xia Y Y，Chen Z S，Gu J C，et al.Indoor full－size model test on stress features of pressure－dispersive prestressed anchorage cable ［J］.Journal of Wuhan University of Technology，2010，32（3）：33－38.