细晶粒高强钢筋混凝土梁受弯性能试验与参数分析

葛文杰，张继文，曹大富，戴 航

（1.扬州大学 建筑科学与工程学院，江苏 扬州225127；2.东南大学 土木工程学院，南京210096）

随着经济的发展，高强度钢筋在混凝土结构中得到广泛使用。目前在国际上使用的是400MPa等级以上建筑钢筋，中国混凝土结构设计规范GB 50010－2010已将 HRBF400级、HRBF500级钢筋列为现行混凝土结构的主导钢筋。高强度钢筋虽然提高了钢筋的强度和结构的承载力，降低了用钢量，但是，使用高强度钢筋可能会造成钢筋混凝土构件出现较大裂缝或挠度而无法满足正常使用极限状态的要求。配置高强度钢筋的混凝土结构在正常使用阶段能否满足结构适用性和耐久性的要求，是高强度钢筋应用于实际工程应解决的重要问题之一。因此，研究高强度钢筋混凝土结构的受力性能具有重要的理论和工程实际意义。

其他国家学者对高强度钢筋混凝土梁的研究较早，Guralnick［1］对高强钢筋T形截面混凝土梁受弯性 能 进 行 了 研 究，Hognestad 等［2］、Kaar等［3］、Timms［4］对高强钢筋混凝土梁受弯、裂缝性能进行了研究，Kyoto等［5］对单向和反复加载下高强钢筋混凝土梁在正常使用极限状态和承载力极限状态下的结构性能进行了研究，Matsumoto等［6］对配置了11种钢筋类型的T形截面高强钢筋混凝土梁进行了研究，Lorrain等［7］对高强钢筋混凝土梁进行了数值模拟分析，Mast等［8］提出了一种适用于高强钢筋混凝土梁承载力的计算方法。中国对于高强钢筋混凝土梁的研究基本处于起步阶段。天津大学的王铁成等［9］、李艳艳等［10］对配置500MPa钢筋的混凝土梁和配有蒙皮钢筋的梁受弯、受剪性能进行了试验研究。青岛理工大学的王命平等［11］通过对比试验研究，建议500MPa级带肋碳素钢筋混凝土简支梁的挠度、裂缝均按现行规范进行计算，但挠度值应乘以扩大系数fy／300（建议取fy＝420MPa）。华侨大学的王全凤等［12］分析了HRB500级钢筋和高强混凝土匹配下的梁的破坏形态、变形特点和承载性能。同济大学的苏小卒等［13］、李志华等［14］、赵勇等［15］对高强钢筋混凝土梁和配表层钢筋的高强钢筋混凝土梁的短期裂缝、刚度进行了研究。江苏大学的陆春华等［16］建议从降低最大裂缝宽度保证率和调整计算钢筋应力2个方面对配置HRB500高强钢筋的受弯构件裂缝宽度计算方法进行适当的修正。

目前中国大部分研究者根据试验研究对钢筋混凝土结构设计理论中的某些参数（如构件受力特征系数acr，平均裂缝间距计算公式中的系数，长期荷载作用下的裂缝宽度扩大系数τl，钢筋应变不均匀系数ψ等）进行了修正，或将计算公式乘以修正系数（如挠度乘以fy／300、1.25，最大裂缝宽度乘以0.9，相对承载力刚度修正系数aB）。本文从正常使用极限状态出发，推导了裂缝／挠度控制条件下的承载力计算公式并进行了参数分析，并对梁的延性及耗能性能也进行了分析。

1 试验概况

设计制作了HRBF400级钢筋、HRBF500级钢筋混凝土梁弯曲破坏构件各4根，构件的截面尺寸及配筋见表1。钢筋的力学性能见表2。

表1 构件尺寸及配筋

表2 钢筋力学性能

2 裂缝性能

2.1 最大裂缝宽度计算

试验测得试验梁在短期荷载作用下最大裂缝宽度随荷载的变化曲线如图1所示。

图1 各试验梁荷载－裂缝宽度曲线

从图1可以看出，细晶粒高强钢筋混凝土梁开裂时初始裂缝宽度很小，从开裂荷载到屈服荷载，裂缝宽度近似按线性增大，达到屈服荷载后裂缝宽度急剧增大；混凝土结构设计规范GB 50010—2002在计算最大裂缝宽度时取荷载效应的标准组合，一般情况下荷载效应标准组合约为极限荷载的80%，试验梁在达到短期荷载最大裂缝宽度控制值ws，max＝0.2mm时，M／Mu的值基本大于0.8。混凝土结构设计规范GB 50010—2010在计算最大裂缝宽度时取荷载效应的准永久组合，一般情况下荷载效应准永久值为标准值的80%，试验梁在达到短期荷载最大裂缝宽度控制值ws，max＝0.2mm时，M／Mu的值全部大于0.64。表明在正常使用条件下，HRBF筋混凝土梁在荷载效应的标准组合下和准永久组合下裂缝宽度都满足规范要求。

矩形截面钢筋混凝土受弯构件在短期荷载作用下的最大裂缝宽度（mm）可按下列公式计算：

式中：acr为构件受力特征系数，对受弯构件，2002版规范与2010版规范规定短期荷载作用下的取值分别为1.4和1.27；ψ为裂缝间纵向受拉钢筋应变不均匀系数，当ψ＜0.2时，取ψ＝0.2。当ψ＞1时，取ψ＝1；σs为纵向受拉钢筋的应力；Es为钢筋弹性模量。β为构件受力特征系数，对于受弯构件，β＝1.0；c为最外层纵向受拉钢筋外边缘至受拉区底边的距离，mm。当c＜20时，取c＝20。当c＞65时，取c＝65；deq为受拉区纵向钢筋的等效直径，mm；di为受拉区第i种纵向钢筋的公称直径，mm；ni为受拉区第i种纵向钢筋的根数；vi为受拉区第i种纵向钢筋的相对粘结特性系数。ρte为按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率，在最大裂缝宽度计算中，当ρte＜0.01时，取ρte＝0.01；Ate为有效受拉混凝土截面面积；As为受拉区纵向非预应力钢筋截面面积。

钢筋混凝土受弯构件受拉区纵向钢筋的应力可按式（6）试算。

短期荷载作用下的最大裂缝宽度的理论计算值与与试验实测值对比见表3。

表3 短期荷载作用下最大裂缝宽度

续表3

由表3并结合图1可以看出，当M／Mu的值达到0.8时，短期荷载作用下的最大裂缝宽度实测值wmax，se均小于0.2mm，表明HRBF筋混凝土梁在正常使用条件下裂缝宽度满足规范要求，但当M／Mu的值还未达到0.8时，根据规范计算出的短期荷载作用下的最大裂缝宽度值wmax，se基本大于0.2mm；2002版规范关于短期荷载作用下最大裂缝宽度的计算值与实测值比值的均值为1.19，变异系数为0.21，2010版规范关于短期荷载作用下最大裂缝宽度的计算值与实测值比值的均值为1.07，变异系数为0.21，理论值普遍大于实测值。

2.2 裂缝控制下承载力计算

短期荷载作用下最大裂缝宽度应满足

将式（1）～（6）代入可得由最大裂缝宽度控制的承载力计算公式为：

当M＜0.35ftbh时，

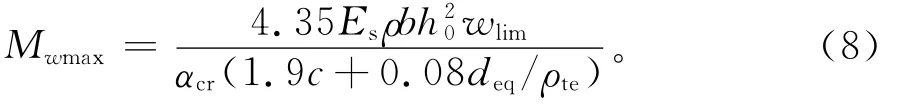
当0.35ftbh02≤M≤3.11ftbh时，

当M＞3.11ftbh时，

将计算所得的由最大裂缝宽度控制的承载力除以构件的极限承载力得M／Mu，称为构件承载力利用系数。由式（8）～（10）可计算得到不同钢筋直径、混凝土保护层厚度下不同配筋率构件的承载力利用系数。其中，图2为HBRF400、HBRF500级钢筋混凝土梁，钢筋直径分别取16、20mm，混凝土保护层厚度分别取20、30mm，混凝土强度分别取C40、C50时构件承载力利用系数随配筋率变化曲线，图中第1个数值代表钢筋强度，第2个代表钢筋直径，第3个代表混凝土保护层厚度，第4个代表混凝土强度等级。

从图2可以看出，随着配筋率的增大，承载力利用系数逐渐提高，构件由裂缝控制逐渐转变为由承载力控制；随着钢筋直径的增大，承载力利用系数逐渐降低；随着混凝土保护层厚度的增大，承载力利用系数逐渐降低；混凝土强度等级对构件承载力利用系数的影响不大；HRBF500级钢筋承载力利用系数要较HRBF400级钢筋低，即随着钢筋强度等级的提高，承载力利用系数有所降低。

图2 各参数对构件承载力利用系数的影响

综上所述，设计HRBF筋混凝土梁时，在满足承载力和耐久性条件下可选用小直径钢筋、较小混凝土保护层厚度来提高构件的承载力利用系数。

3 挠度性能

3.1 挠度计算

各试验梁在不同等级荷载作用下的挠度与跨度的比值如图3所示。

钢筋混凝土梁在长期荷载作用下的的挠度控制值f／l0≤1／200，试验为短期加载，无法考虑荷载的长期作用，取荷载效应准永久值为标准值的80%、准永久组合系数为0.8，2002版规范在计算变形时取荷载效应标准组合，可得在短期荷载作用下的挠度控制值为f／l0≤1／360。从图3可以看出，HRBF400筋混凝土梁M／Mu在达到0.8时f／l0未超过限值，而HRBF500筋混凝土梁M／Mu在未达到0.8时f／l0已经超过限值；新修订的2010版规范为推广细晶粒高强钢筋在工程中的应用，在计算变形时取荷载效应准永久组合，可得在短期荷载作用下的挠度控制值为f／l0≤1／400，从图3可以看出，HRBF400筋混凝土梁M／Mu在达到0.64时f／l0未超过限值，而 HRBF500筋混凝土梁M／Mu在未达到0.64时f／l0已经超过限值。说明HRBF400筋混凝土梁的挠度能够满足规范要求，而HRBF500级混凝土梁不能够满足规范要求，在设计时要加强对挠度进行验算。

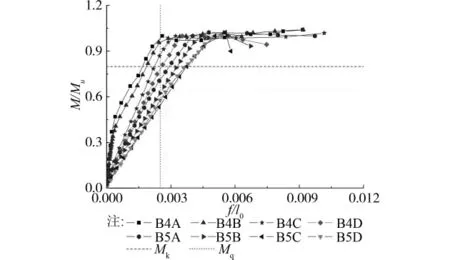
图3 各试验梁荷载－跨中挠度宽度曲线

在荷载作用下，简支梁跨中挠度计算公式为：

其中：a为系数，与荷载的作用形式有关；M为跨中最大弯矩；l0为计算跨度；Bs为短期荷载作用下构件最大弯矩处的截面刚度，混凝土结构设计规范规定其计算公式如式（12）。

式中：ρ为纵向受拉钢筋配筋率；γf'为受压翼缘截面面积与腹板有效截面面积的比值。

各试验梁在短期荷载作用下挠度实测值与根据规范计算的理论值对比见图4（以试件B4D、B5D为例），其中，E表示试验实测值，T表示规范计算值。从图4可以看出，理论计算值与试验实测值吻合较好，且规范计算值基本大于试验实测值，偏于安全。

3.2 挠度控制下承载力计算

为满足正常使用条件下的适用性的要求，对结构构件其最大挠度进行控制

式中：f为荷载作用下的最大挠度；l0为构件的计算跨度，β为系数，对于不同结构形式、不同跨度取相应的值。

由式（11）与式（13）可得，由挠度控制的荷载设计值为：

图4 挠度实测值与计算值比较

将式（12）代入并整理得：

当M＜0.35ftbh时，

当0.35ftbh02≤M≤3.11ftbh时，

即

当M＞3.11ftbh时，

同裂缝控制条件下构件的承载力利用系数，可得挠度控制条件下构件的承载力利用系数。由式（15）～（18）可计算得到不同高跨比、混凝土强度等级下随着配筋率的变化构件的承载力利用系数。

图5为HBRF400级钢筋、HBRF500级钢筋混凝土梁，高跨比分别取1／8、1／10，混凝土强度分别取C40、C50时，构件的承载力利用系数随着配筋率变化曲线。由图5可以看出，随着配筋率的提高，构件的承载力利用系数逐渐降低并趋于稳定，构件由承载力控制转变为由挠度控制；随着高跨比的减小，构件的承载力利用系数逐渐降低；混凝土强度对构件的承载力利用系数影响不大；HRBF500级构件的承载力利用系数较HRBF400级构件低，即随着钢筋强度等级的提高，构件的承载力利用系数有所降低。

4 延性及耗能性能

延性是指截面或构件在承载能力没有显著下降的情况下承受变形有能力，或者说延性的含义是破坏以前截面或者构件能承受很大的后期变形。常用来Δu／Δy、φu／φy，或者θu／θy表示延性比，延性比大说明截面或构件的延性好，反之延性就较差。脆性破坏是到达最大承载能力后，突然破坏，后期变形能力很小。

图5 各参数对构件承载力利用系数的影响

借助计算机计算程序，可求出弯矩－曲率关系。将求得的数值代入式（19）求得构件的延性us随配筋率ρ的变化如图6所示，其中，C40 335表示混凝土强度等级为C40、钢筋强度为 HRB335，其它类似。构件截面尺寸采用本次试验设计尺寸，材料强度均采用本次试验实测值。

图6 构件延性随配筋率变化曲线

普通钢筋混凝土结构设计中要求延性在3以上，根据图6可以看出，在经济配筋率范围内，HRBF筋混凝土梁的延性基本能满足要求。

M－φ曲线下面所包含的面积代表“吸收的能量”，如近似地取屈服弯矩等于极限弯矩，并且忽略屈服前裂缝的影响，这样M－φ曲线下吸收的能量可用下式计算

钢筋屈服前吸收的能量可用下式计算

式中：Δy、φy、θy分别为钢筋屈服时变形、曲率、转角；Δu、φu、θu分别为破坏时的变形、曲率、转角；My为钢筋屈服时的弯矩。

计算得到的构件吸收的能量ws、屈服前吸收的能量we随配筋率ρ变化的曲线如图7所示。

图7 构件w－ρ曲线

从图7可以看出，HRBF筋混凝土梁的耗能能力在较低配筋率时与普通钢筋混凝土梁相近，但随着配筋率的提高，其耗能能力较普通钢筋混凝土梁降低的快。HRBF筋混凝土梁在同等配筋率下其弹性阶段的耗能能力要较普通钢筋混凝土梁的耗能能力要高，且随着配筋率的增大而提高。

5 结 论

1）HRBF筋混凝土梁在短期荷载作用下的最大裂缝宽度实测值满足规范要求，但计算值不满足。推导了HRBF筋混凝土梁在裂缝控制条件下的承载力计算公式，提出了构件承载力利用系数的概念。分析表明随着配筋率的增大，承载力利用系数逐渐提高，构件由裂缝控制逐渐转变为由承载力控制；随着钢筋直径、混凝土保护层厚度的增大，承载力利用系数逐渐降低；混凝土强度等级对构件承载力利用系数的影响不大；HRBF500级钢筋承载力利用系数要较HRBF400级钢筋低。

2）HRBF400级钢筋混凝土梁在正常使用条件下的挠度能满足规范要求，但HRBF500级钢筋混凝土梁不能够满足规范要求。推导了挠度控制条件下的承载力计算公式。分析表明随着配筋率的提高，构件的承载力利用系数逐渐降低并趋于稳定，构件由承载力控制转变为由挠度控制；随着高跨比的减小，构件的承载力利用系数逐渐降低；混凝土强度对构件的承载力利用系数影响不大；随着钢筋强度等级的提高，构件的承载力利用系数有所降低。

3）建议在满足承载力和耐久性的条件下可使用较小直径的钢筋、较小的混凝土保护层厚度以提高构件的承载力利用系数。

4）在经济配筋率范围内，HRBF筋混凝土梁的延性基本能满足要求。HRBF筋混凝土梁的耗能能力在较低配筋率时与普通钢筋混凝土梁相近，随着配筋率的提高，其耗能能力较普通钢筋混凝土梁降低的快，但同配筋率下，HRBF筋混凝土梁在弹性阶段的耗能能力较普通钢筋混凝土梁要高，且随着配筋率的提高而增大。

［1］Guralnick S A.High－strength deformed steel bars for concrete reinforcement［J］.American Concrete Institute Journal，1960，32（9）：241－282.

［2］Hognestad E，Gaston J R.High strength bars as concrete reinforcement ［J］.Portland Cement Association－Research and Development Laboratories，1962，9（3）：2－12.

［3］Kaar P H，Mattock A H.High strength bars as concrete reinforcement－4.Control of cracking ［J］.Portland Cement Association－Research and Development Laboratories，1963，5（1）：15－38.

［4］Timms A G.High strength steel bars as concrete reinforcement［J］.Modern Concrete，1964，28（8）：28－31.

［5］Okada K，Kobayashi K，Miyagawa T，et al.Reinforced concrete members with high strength steel bars ［J］.Japan Society of Civil Engineers－Transactions，1985（6）：567－574.

［6］Matsumoto Y，Nakamura S，Kono K，et al.Flexural behavior of reinforced concrete beams with high strength deformed bars ［J］.Japan Society of Civil Engineers Transactions，1965，122（10）：1－28.

［7］Lorrain M，Maurel O，Boukari S，et al.Numerical and experimental analysis of high strength concrete beams reinforced with high yield steel bars submitted to flexure［J］.Materials and Structures，1999，32（12）：708－718.

［8］Mast R F，Dawood M，Rizkalla S H，et al.Flexural strength design of concrete beams reinforced with highstrength steel bars ［J］.ACI Structural Journal，2009，106（4）：551－552.

［9］王铁成，李艳艳，戎贤.配置500MPa钢筋的混凝土梁受弯性能试验［J］.天津大学学报，2007，40（5）：507－511.Wang T C，Li Y Y，Rong X.Test for bending behavior of reinforced concrete beam with 500MPa steel bar［J］.Journal of Tianjin University，2007，40（5）：507－511.

［10］李艳艳，崔武文，戎贤.高强钢筋混凝土梁裂缝控制试验研究［J］.混凝土，2011（5）：132－135.Li Y Y，Cui W W，Rong X.Experimental research on crack control of concrete beams reinforced with HRB500［J］.Concrete，2011（5）：132－135.

［11］王命平，张自琼，耿树江.500MPa级带肋碳素钢筋混凝土简支梁的受弯试验［J］.工业建筑，2007，37（8）：39－42.Wang M P，Zhang Z Q，Geng S J.Experiment of reinforced concrete simply supported beam with 500 MPa ribbed carbon bars under bending ［J］.Industrial Construction，2007，37（8）：39－42.

［12］王全凤，刘凤谊，杨勇新，等.HRB500级钢筋混凝土简支梁受弯试验［J］.华侨大学学报：自然科学版，2007，27（3）：300－303.Wang Q F，Liu F Y，Yang Y X，et al.Experimental investigation on flexural behavior of simple supported RC beams with grade HRB500reinforcement T ［J］.Journal of Huaqiao University：Natural science，2007，27（3）：300－303.

［13］苏小卒，李志华，赵勇，等.配置表层钢筋的混凝土梁裂缝和刚度试验探讨研究［J］.建筑结构学报，2009，30（1）：62－67.Su X Z，Li Z H，Zhao Y，et al.Experimental research on crack width and stiffness of reinforced concrete beams with skin reinforcement ［J］.Journal of Building Structures，2009，30（1）：62－67.

［14］李志华，苏小卒，赵勇.配置高强钢筋的混凝土梁裂缝试验研究［J］.土木建筑与环境工程，2010，32（1）：51－55.Li Z H，Su X Z，Zhao Y.Experimental analysis of cracking behavior of concrete beams reinforced with high－strength bars［J］.Journal of Civil，Architectural ＆Environmental Engineering，2010，32（1）：51－55.

［15］赵勇，王晓锋，苏小卒，等.配置500MPa钢筋的混凝土梁裂缝试验研究［J］.同济大学学报：自然科学版，2011，39（1）：29－34.Zhao Y，Wang X F，Su X Z，et al.Experimental research on crack spacing and width of reinforced concrete beams with 500MPa steel bars ［J］.Journal of Tongji University：Natural Science，2011，39（1）：29－34.

［16］陆春华，金伟良，延永东.正常使用状态下 HRB500钢筋混凝土梁受弯性能试验［J］.江苏大学学报：自然科学版，2011，32（3）：350－354.Lu C H，Jin W L，Yan Y D.Experiment for flexural behavior of HRB 500rebar reinforced concrete beam under serviceability state ［J］.Journal of Jiangsu University：Natural Science Edition，2011，32（3）：350－354.