某体育场悬挑屋盖表面脉动风压空间相关特性

陈朝晖，张海永，陈 丰

（1.重庆大学a.土木工程学院；b.重庆大学山地城镇建设与新技术教育部重点实验室，重庆400045；2.机械工业第三设计研究院，重庆400039；3.湖南省建筑设计院，长沙410011）

在体育场悬挑屋盖结构的风致响应计算及确定静力等效风荷载时，风荷载的空间相关特性一直是研究的重点之一。Vickery［1］和 Rocha［2］通过对体育场悬挑屋盖结构不同位置点的风压同步测试，得到了脉动风压的相关系数，数据显示不同位置点的空间相关性随距离增加而减小。张朝晖［3］对体育场悬挑屋盖上、下表面脉动风压的相关系数进行了分析，验证了上、下表面同步测试的必要性。目前，脉动风速相干函数的研究对脉动风压相干函数有很大的借鉴意义，但 Kareem［4］、顾明［5］通过研究都得出了脉动风压相干性大于脉动风速相干性的结论。Davenport［6］研究发现，空间两点处脉动风速相关性与频率及两点间距离有关，其空间相干函数可用指数形式表示。他的分析指出，垂直来流方向测点间的相干性要大于平行来流方向。Saranyasoontorn［7］把几种经典相干函数模型进行对比分析，得出它们的适用性随两点间距、风速等因素而变化的结论。与高层建筑脉动风压相干函数不同，悬挑屋盖脉动风压相干函数有其本身的特征湍流作用，Irwin［8］分析了涡旋脱落对不同类型建筑的影响。汪丛军［9］对体育场环状悬挑屋盖的试验数据进行了分析，采用Davenport水平相干函数公式对相干函数曲线进行了拟合。Nakamura［10］对体育场悬挑屋盖进行了刚性模型试验和气弹模型试验，朱川海［11］对独立弧形主看台挑篷进行了刚性模型试验，其中气弹性模型试验比刚性模型试验结果吻合度更好，在试验基础上两人分别由风压的互谱及相干性分析得到了适用于体育场屋盖结构的形式相似的相干函数公式。

笔者以某体育场为研究对象，进行了同步测压刚性模型风洞试验，对体育场悬挑屋盖结构不同区域平行来流方向、垂直来流方向排列的测点间脉动风压空间相关特性进行了分析，分析了涡旋脱落的影响，对脉动风压相干函数曲线进行拟合，得到的该类结构相干函数公式为建立更为精细的气弹模型提供了参考依据。

1 风洞试验及其数据概况

湖南郴州体育场东西向长256.8m，南北向长217.8m。上部钢结构屋盖形式为环形悬挑结构，最大悬挑长度21.9m；屋盖最大标高为39.0m，最低标高为26.5m。为了研究该体育场屋盖的脉动风压空间相干特性，在中国空气动力研究与发展中心低速所12m×16m边界层风洞中进行了体育场屋盖上、下表面同步测压风洞试验。试验风速为10m／s，采样频率为156.25Hz，采样时间步数为8 192步。

根据建筑所在场地及其周边环境，采用尖劈和粗糙元模拟中国规范中B类风场的风剖面，地貌粗糙度系数为0.16。综合考虑实际建筑物大小和风场模拟的要求，模型几何缩尺比取为1∶100，模型总高度为0.39m。试验中实测地貌粗糙度系数为0.168，风洞试验阻塞率小于5%，湍流度风剖面依据日 本 建 筑 规 范 （AIJ）［12］，参 考 点 湍 流 强 度 为16.5%。屋盖上、下两层分别采用ABS板和航空板制作，厚度均为1mm；两层之间留有2cm的空隙布置测压管路。风洞试验模型如图1所示。根据结构外形特征和试验要求，在屋盖上、下表面对应位置布设270对即540个测压孔。将屋盖用两个对称轴分为逆时针排列的A、B、C、D 4个区，如图2所示。其中A、D区的测压点位置及其编号如图3所示。

图1 风洞试验模型

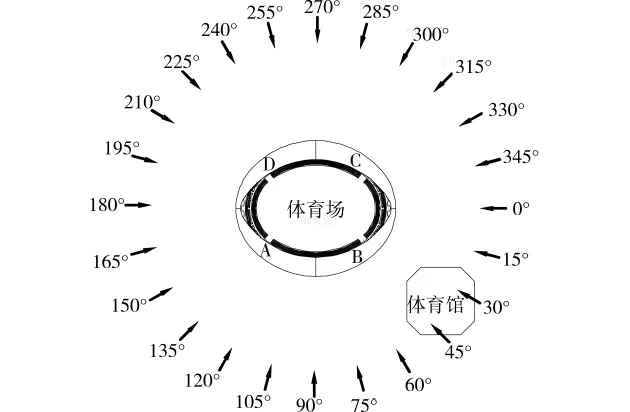
图2 试验模型风向角示意图

图3 屋盖A、D区测压点平面示意图

为研究环形悬挑屋盖的空间相关特性，对平行来流方向测点间、垂直来流方向测点间的相关系数和相干函数分别进行分析。定义测点间连线与来流风向夹角小于15°为平行来流方向测点，与来流风向的垂直线夹角小于15°为垂直来流方向测点。另外，鉴于环形悬挑屋盖不同区域的空间相关特性差异较大，把整个屋盖分为4个区域，分别为上风向屋盖、下风向屋盖和两个侧面屋盖，它们的界线是与通过体育场中心点的来流风向线夹角为45°的两条互相垂直的线。如图4所示。试验中体育场旁边的体育馆在某些风向角下会对体育场悬挑屋盖的风压产生干扰，在文献［3］中分析了干扰效应，本文则只在无干扰的风向角下对体育场屋盖的脉动风压相关特性进行分析，故本文选取225°风向角进行相关分析。屋盖上、下表面都受到风荷载作用，所以计算不同位置的脉动风压相关系数和相干函数时所用的风压时程为上、下表面叠加所得净风压时程。图5为225°风向角下所测得上风向屋盖测点D50的净风压时程。

图4 屋盖平行、垂直来流方向测点及4区域划分示意图

图5 225°风向角时上风向屋盖测点D50净风压时程

2 时域下脉动风压相关系数

模型表面不同位置测点间的脉动风压相关系数是两点间空间相关性在时域下所作的度量，对频域下两点间空间相干性的分析有指导作用。相关系数Corij的定义如下：

式中，σij为i、j两点的风压协方差，σi和σj分别为i、j两点的风压根方差。

2.1 平行来流方向排列的测点间相关系数

考虑到环状悬挑屋盖的形状特征，这些测点分别取自上风向屋盖区域、下风向屋盖区域及侧面屋盖区域。表1～3列出了体育场模型屋盖上3个不同区域测点的脉动风压平行来流方向排列的测点间相关系数。左上角和右下角分别表示两列平行来流方向测点的结果。

表1 上风向屋盖平行来流方向测点间相关系数

表2 下风向屋盖平行来流方向测点间相关系数

表3 侧面屋盖平行来流方向测点间相关系数

由表1～3可知：平行来流方向测点间脉动风压相关系数随两点间距的增加而减小；同一部位测点间相关系数均是正值；下风向屋盖的平行来流方向测点间相关性最高，上风向屋盖次之，侧面屋盖最低。

此外，对比上风向屋盖测点：由前缘D48与D47两点、中部D47与D46两点、后缘D46与D45两点的3个相关系数可知，后缘测点的相关性明显高于前缘测点相关性，从前缘到后缘逐渐增大；但屋盖后缘D46与D45两点之间相关系数不是很大，说明屋盖迎风前缘发生涡旋脱落后，由于屋盖沿平行来流方向的长度小于再附流的长度，再附着并不充分。在下风向屋盖测点间的相关系数中，对比前缘B33和B34两点、中部B34和B35两点、后缘B35和B36两点的3个相关系数可知，屋盖前缘测点的相关性明显高于后缘测点的相关性，说明此类形式屋盖气流涡旋从迎风前缘脱落后，在B33测点以前就再附着，所以前缘部位相关系数很大，中部小，而后缘部位又比中部略有增加。侧面屋盖的相关系数呈现前后大、中间小的趋势，表明侧面屋盖表面存在分离泡并迅速再附着。并且，侧面屋盖的两个边缘相关性分布一致，比中部相关性整体上略低。

2.2 垂直来流方向排列的测点间相关系数

测点分别取自上风向屋盖区域、下风向屋盖区域及侧面屋盖区域。表4～8列出了体育场模型屋盖上3个不同区域测点的脉动风压垂直来流方向测点间的相关系数。表的左上角和右下角分别表示两列垂直来流方向测点的结果。

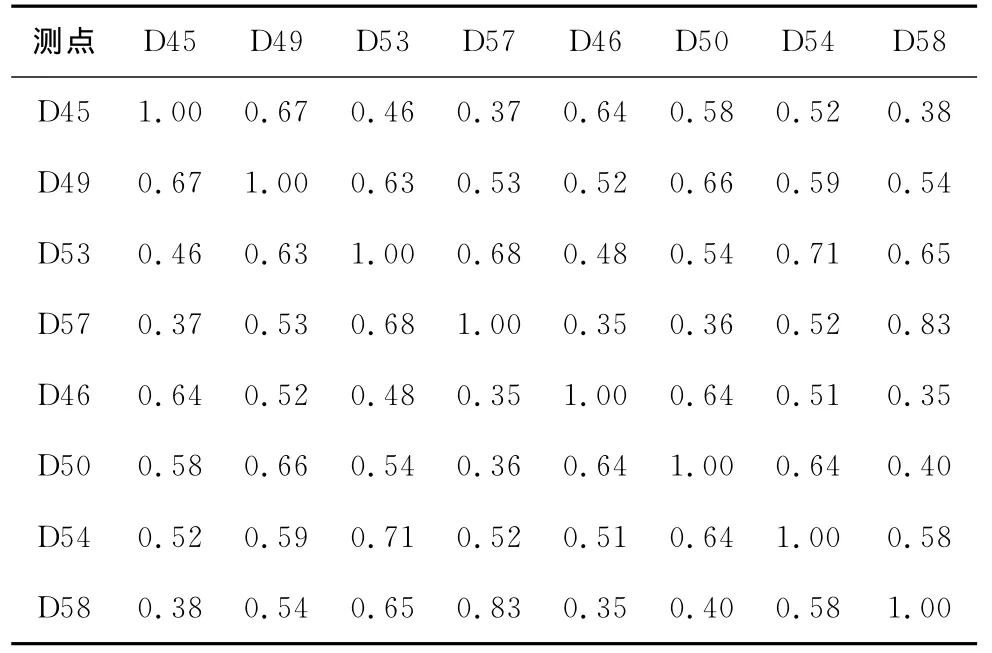
表4 上风向屋盖后缘和中部垂直来流方向测点间相关系数

表5 上风向屋盖中部和前缘垂直来流方向测点间相关系数

续表5

表6 下风向屋盖前缘和中部垂直来流方向测点间相关系数

表7 下风向屋盖中部和后缘垂直来流方向测点间相关系数

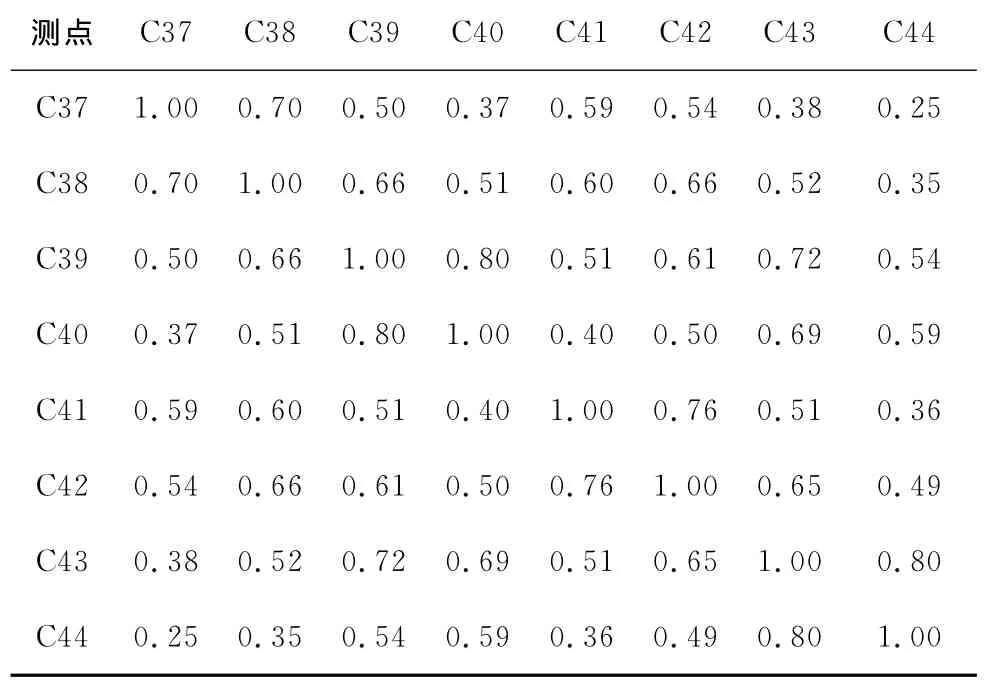
表8 侧面屋盖脉动风压垂直来流方向测点间相关系数

各区域的垂直来流方向测点间相关性由表可见：1）脉动风压垂直来流方向测点间相关性同样随距离的增加而减小。2）同一部位的测点间相关系数均是正值。下风向屋盖的垂直来流方向测点间相关性最高，侧面屋盖次之，上风向屋盖最低。3）表4～7中左上角和右下角的数据大小分布均匀，说明上风向屋盖及下风向屋盖的垂直来流方向测点间相关性水平相当。4）上风向屋盖区域在前缘和中部的交界区垂直来流方向测点间相关性较低，这是由于涡旋脱落在此产生了分离泡。5）下风向屋盖区域从前缘到后缘相关性都很均匀。6）表8中，对比边缘C41与C42两点、C43与C44两点、中部C42与C43两点的3个相关系数可知，侧面屋盖边缘比中部相关性强。这是因为侧面屋盖上的分离泡位于中部。

3 频域下脉动风压相干函数

屋盖表面脉动风压频域相干函数反映了风荷载在频域内的空间相关特性，是影响风致响应的因素之一。两点的相干函数Cohij（n）表达式为

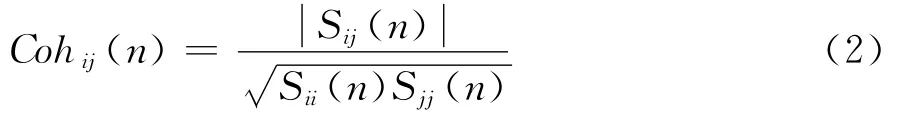
式中：n为频率；Sij（n）为i、j两点的互谱密度函数，Sii（n）、Sjj（n）为自谱密度函数。

文献［9］分析了相干函数随两点间距离增大而减小的特性，本试验分析得出相同的结论，本文对屋盖各区域平行来流方向、垂直来流方向排列的测点的相干特性进行分析。由于试验仪器的限制，试验只测到0～78.125Hz之间的风压谱，进而只能计算此区间的相干函数。但由文献［6－9］可知，78.125 Hz以后的相干函数曲线也呈总体下降趋势。

Davenport相干函数公式和Nakamura相干函数公式是目前常用的脉动风压相干函数公式，分别见式（3）和式（4）。

式中：n为频率；δ为i、j两点的水平距离；U为该高度处的来流平均风速；C为相干函数衰减指数。文献［9］中针对沈阳奥林匹克体育场悬挑屋盖，建议Davenport相干函数公式中C取6；文献［7］中针对日本大阪体育场悬挑屋盖，Nakamura把C取为4.2。另外，Nyi等［13］、黄东梅等［14］、魏奇科等［15］也分别提出了针对大跨屋盖和高层建筑的脉动风压相干函数新数学模型，但都参数较多或形式复杂。

3.1 上风向屋盖相干函数分析

上风向屋盖平行来流方向、垂直来流方向排列的典型测点的相干函数曲线列于图6～9。图6、7反映了90度风向角下平行来流方向测点间相干函数规律：1）随着频率的增加，相干函数呈明显的下降趋势。2）曲线在50Hz左右幅值较高，这与文献［13］试验结果相同。分析可知，此段曲线正好处在涡旋脱落频率附近，说明上风向屋盖测点脉动风压的形成既有来流脉动风的成分，也有明显的涡旋脱落的影响。3）在低频部分，迎风前缘测点D1、D2的相干函数要高于后缘测点D3、D4的相干函数，且从前缘到后缘呈现出逐步减小的趋势，这与相关系数的变化规律相符。图8、9反映了225度风向角下垂直来流方向测点间相干函数特性：1）随着频率的增加，相干函数呈明显的下降趋势。2）曲线在50Hz左右幅值较高。3）从前缘到后缘，相干函数水平相当。因此，上风向屋盖的平行来流方向、垂直来流方向排列的测点间相干函数可以用相同的函数形式进行拟合。

图6 上风向屋盖平行来流方向测点间相干函数曲线

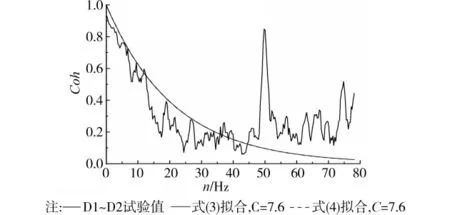
图7 上风向屋盖平行来流方向测点间相干函数拟合

图8 上风向屋盖垂直来流方向测点间相干函数曲线

图9 上风向屋盖垂直来流方向测点间相干函数拟合

如图7所示，对式（3）和式（4）的拟合情况进行对比，发现两公式拟合曲线近乎重合，且基本符合相干函数曲线。另外，对其它区域的相干函数曲线进行拟合，两公式的结果也近乎重合，而且有些拟合结果显示，Davenport相干函数公式在高频处的拟合要略微好些。这是因为Nakamura相干函数公式中的余弦项随着频率增大而变小。因此，采用形式更为简洁的Davenport相干函数公式进行拟合。统计拟合结果可知，对所研究的悬挑屋盖，上风向屋盖平行来流方向相干函数拟合公式中的衰减指数C取7.5左右；上风向屋盖垂直来流方向相干函数拟合公式中C取5.0～5.5之间，如图9所示。

3.2 下风向屋盖相干函数分析

下风向屋盖上平行来流方向、垂直来流方向排列的典型测点间的相干函数列于图10～13。由图10、11反映的平行来流方向测点间相干函数规律可知：1）随着频率的增加，相干函数呈明显的下降趋势，在低频部分尤其显著。2）在涡旋脱落频率附近出现幅值较高的窄波峰，说明上风向屋盖测点脉动风压的形成既有来流脉动风的成分，也有明显的涡旋脱落的影响；3）中部和后缘相干函数水平相当，前缘水平略高，这与相关系数的变化规律相同。采用（3）式的相干函数形式进行拟合是可行的，并且衰减指数C取9.0左右。

图10 下风向屋盖平行来流方向测点间相干函数曲线

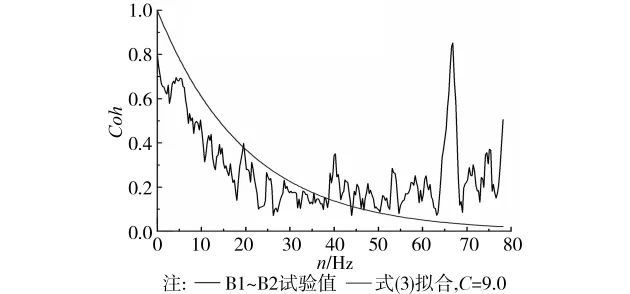
图11 下风向屋盖平行来流方向测点间相干函数拟合

图12 下风向屋盖垂直来流方向测点间相干函数曲线

图13 下风向屋盖垂直来流方向测点间相干函数拟合

由图12～13可知，下风向屋盖的垂直来流方向测点间相干函数整体水平要比平行来流方向测点间相干函数高；从前缘到后缘相干函数水平相当，这与相关系数的变化规律相符；与下风向屋盖的平行来流方向测点间相干函数不同处还在于，低频部分衰减更加显著。但是采用式（3）的相干函数形式依然可行。图13拟合的结果表明，忽略存在试验误差的高频部分，此相干函数公式对下风向屋盖脉动风压垂直来流方向测点间相干函数曲线的拟合在低频处（40Hz以下）吻合较好，但高频处略低。衰减指数C取3.5～4.5之间。

3.3 侧面屋盖相干函数分析

侧面屋盖的平行来流方向、垂直来流方向排列的典型测点间相干函数列于图14～17。由平行来流方向测点间相干函数图14、15可知：1）随着频率的增加，相干函数呈明显的下降趋势，在低频部分尤其显著。2）边缘相干函数整体上比中部略大，符合相关系数的变化规律。类似（3）式的相干函数形式依然适用。统计结果表明，平行来流方向测点间相干函数拟合公式中衰减指数C取4.5～5.0之间。

图16、17反映了侧面屋盖垂直来流方向测点间相干函数规律：1）随着频率的增加，相干函数呈明显的下降趋势。2）边缘相干函数整体上比中部略大，符合相关系数的变化规律。3）整体水平比侧面屋盖平行来流方向测点间相干函数高，而且在各区域的平行来流方向、垂直来流方向测点间的相干函数中是整体水平最高的。图17拟合的结果表明，衰减指数C取5.5左右。

图14 侧面屋盖平行来流方向测点间相干函数曲线

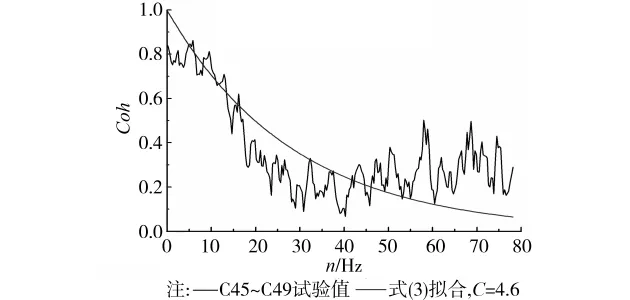
图15 侧面屋盖平行来流方向测点间相干函数拟合

图16 侧面屋盖垂直来流方向测点间相干函数曲线

图17 侧面屋盖垂直来流方向测点间相干函数拟合

4 与现有风压相关特性研究结论的比较

对大跨度体育场屋盖测点相关系数研究发现，由于体型复杂，其脉动风压的空间相关特性也很复杂。文献［15］研究了高层建筑的水平相关系数，以迎风面为例，相关系数值最小为0.89，且不同位置测点的相关系数值差别很小。研究大跨度体育场屋盖发现，相关系数值总体上比高层建筑的要小，且由于屋盖复杂形状的影响，相关系数值分布在0.4～0.9之间一个较大的范围内。这与文献［2］中对体育场悬挑屋盖风压相关系数的研究结论一致。研究发现，在两点间距相同的情况下，平行来流方向排列与垂直来流方向排列的两点风压相关系数明显不同，这一点以往研究鲜有涉及。

研究大跨度体育场屋盖测点相干函数时发现，测点所在屋盖区域的不同、测点是平行还是垂直来流方向排列都对相干函数曲线有重要影响。因此，与高层建筑的空间相干特性不同，在研究大跨度屋盖结构风压相干特性时，不能在仅考虑两点间距的情况下得出一个对屋盖各区域都适用的相干函数数学模型。与高层建筑的水平相干函数曲线相比，大跨度体育场屋盖的相干函数曲线从低频到高频的减小趋势更为显著。文献［15］同样用Davenport相干函数的数学模型对高层建筑的水平相干函数曲线进行了拟合，以迎风面为例，衰减指数C基本都在2～4之间，明显低于本文拟合所取的衰减指数C。而且从拟合结果看出，由于测点所在的屋盖区域不同和测点沿平行或垂直来流方向排列的方式不同，衰减指数C取值有显著不同。文献［9］中对于体育场悬挑屋盖，C值统一取为6。而本文的研究显示，对于平行来流方向排列的测点，C的取值一般大于6；对于垂直来流方向排列的测点，C的取值一般小于6。

综上所述，大跨度体育场屋盖空间相关特性有其自身的特点，即测点所在的屋盖区域、测点是平行或垂直来流方向排列对相关特性影响较大。此外，与高层建筑相比，涡旋脱落对大跨度体育场屋盖相干函数的影响更为显著，体现在体育场屋盖风压相干函数曲线中的窄波峰的峰值更高。

5 结 论

1）各屋盖区域的垂直来流方向测点间相关性均高于平行来流方向测点间相关性，上风向屋盖的相关性略低于侧面屋盖相关性，而下风向屋盖的相关性最高。这是由于涡旋脱落主要影响平行来流方向相关性，并且从上风向屋盖到下风向屋盖涡旋脱落的影响逐渐减小。

2）相干函数曲线在屋盖各区域都表现出从低频到高频的减小趋势，且低频部分的减小趋势显著。在上风向屋盖，平行来流方向测点间相干性水平略高于垂直来流方向测点。而在下风向屋盖和侧面屋盖，垂直来流方向测点间相干性要高于平行来流方向测点间相干性。

3）上风向屋盖的相干性整体水平表现出从前缘到后缘逐步减小的趋势；下风向屋盖的相干性整体水平表现为中部和后缘相干函数水平相当，前缘水平略高；侧面屋盖的相干性整体水平表现为边缘比中部略大；这均与相关系数的变化规律相同。

4）用Davenport相干函数的数学模型对各区域相干函数曲线进行了拟合，其衰减指数C在各区域取值范围不同。而对下风向屋盖脉动风压垂直来流方向测点间相干函数在40Hz以上部分的拟合曲线偏低，有必要作进一步的研究。另外，由于试验误差的原因，在60～78.125Hz之后的相干函数曲线出现升高的幅值，有必要对该类型屋盖结构做更为精细的气弹模型试验。

［1］Vickery B J，Majowiecki M.Wind induced response of a cable supported stadium roof ［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，42（1－3）：1447－1458.

［2］Rocha M M，Cabral S V S，RIERA J D.A comparison of proper orthogonal decomposition and Monte Carlo simulation of wind pressure data［J］.Journal of Wind Engineering and Industrial Aerodynamic，2000，84（3）：329－344.

［3］张朝晖，陈朝晖，陈丰，等.有干扰的大跨度体育场屋盖表面风荷载特性研究［J］.建筑结构，2012，42（2）：154－158.Zhang Z H，Chen Z H，Chen F，et al.Invesitigation on wind Load characferistics of the large－span cantileveered roof of a stadiun with interference ［J］.Building Structure，2012，42（2）：154－158.

［4］Kareem A.Synthesis of fluctuating along wind loads on buildings［J］.Journal of Engineering Mechanics，1986，112（1）：121－125.

［5］顾明，张建国.高层建筑顺风向脉动荷载相干性研究［J］.土木工程学报，2008，41（11）：18－22.Gu M，Zhang J G.Coherence analysis of along－wind fluctuating loads on high－rise buildings［J］.China Civil Engineering Journal，2008，41（11）：18－22.

［6］Davenport A G.Gust loading factors ［J］.Struct Div ASCE，1967，93（ST3）：11－34.

［7］Saranyasoontorn K，Manuel L，Veers P.A comparison of standard coherence models for inflow turbulence with estimates from field measurements［J］.Journal of Solar Energy Engineering，2004，126（4）：1069－1082.

［8］Irwin P A.Bluff body aerodynamics in wind engineering［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96（6－7）：701－712.

［9］汪丛军.体育场环状悬挑屋盖风荷载特性及风振分析［D］.上海：同济大学，2006.

［10］Nakamura O，Tamura Y，Miyashita K，et al.A case study of wind pressure and wind－induced vibration of a large span open－type roof ［J］.Journal of Wind Engineering and Industrial Aerodynamics，1994，52 （1－3）：237－248.

［11］朱川海.大型体育场主看台挑蓬的风荷载特性与风致响应研究［D］.上海：同济大学，2003.

［12］AIJ Recommendations for Loads on Buildings ［S］.Japan，2004.

［13］Nyi N A，Ye J H.Coherence of wind pressure on domes［J］.Journal of Southeast University：English Edition，2010，1（1）：100－106.

［14］黄东梅，朱乐东.超高层建筑层风力空间相关性数学模型—综合分析法［J］.土木工程学报，2009，42（8）：26－36.Huang D M，Zhu L D.Mathematical model of spatial correlation of wind pressure coefficients for super－tall buildings：comprehensive analysis method ［J］.China Civil Engineering Journal，2009，42（8）：26－36.

［15］魏奇科，李正良，黄汉杰，等.超高层建筑表面脉动风压空间相关特性试验研究［J］.实验流体力学，2010，24（5）：63－69 Wei Q K，Li Z L，Huang H J，et al.Fluctuating pressure correlativity test analysis on super－tall buildings ［J］.Journal of Experiments in Fluid Mechanics，2010，24（5）：63－69.