高速滑行艇升沉纵摇运动的实时数值预报方法研究
2013-02-28王志东凌宏杰
王志东,凌宏杰
(江苏科技大学船舶与海洋工程学院,江苏镇江212003)
滑行艇的流体动力特性研究早在上世纪60年代就引起了众多学者的关注,并且在滑行艇阻力性能预报方面取得了显著的研究成果,提出了一系列滑行艇阻力计算的经验或半经验公式[1-4].近年来以实时求解雷诺时均方程RANS为目标的现代CFD技术被应用到水面高速艇流体动力性能的精确预报,文献[5]基于有限体积方法研究了高速艇的运动特性,其中压力与速度的耦合采用分裂算法,水气交界面的模拟采用VOF方法,采用贴体网格系统数值计算了定常直航时流体作用在高速艇上的力和力矩以及6自由度运动响应,给出了高速艇的运动速度、加速度及其位置,通过与试验对比表明,基于数值求解RANS方程的数值方法可用于指导高速艇的流体动力设计及运动性能预报.文献[6-8]利用非定常RANS方法编制了水面舰艇6自由度运动响应预报程序CFDSHIP-IOWA,求解器采用高阶上风离散格式、PISO压力速度耦合方法k-ε/k-ω两方程湍流模型,其中自由表面追踪技术分别采用VOF方法和Level Set方法,数值预报了水面舰艇在多种航行状态下的自由面绕流场及其运动响应特性,结果优于传统的线性切片理论,同时指出水面波形破碎是引起船舶非线性流体动力载荷的主要原因.
边界元方法[9]也被用于滑行艇模型的水动力性能数值预报,通过开展滑行平板、楔形体、底部斜升体等3种滑行艇模型的计算分析,探讨了不同航速下的压力分布、阻力、升力及波形,与相关试验结果的吻合度较好.
文献[10]利用计算机流体力学软件FLUENT数值模拟了滑行艇在静水中的直航运动,给出了滑行艇阻力随航行速度的变化曲线,探讨了滑行艇底部的压力分布及尾流场;文献[11]建立了高速滑行艇6自由度运动方程,利用Matlab软件开展了滑行艇的运动与姿态控制的仿真预报研究.
文中基于C语言编写了滑行艇升沉纵摇耦合运动预报用户自定义程序,采用预测/修正法求解运动方程,将求解方程嵌入到FLUENT软件中,对5 种不同体积傅汝德数 Fr2=0.9,1.8,2.7,3.6,5.0条件下滑行艇的纵摇与升沉耦合运动特性进行研究.在计算过程中为保证当艇体产生大位移运动时的网格质量,采用弹簧法和局部重构联合作用的运动网格技术,控制艇体表面及外部网格的生长速度和尺度;同时为保证计算精度,对网格重构的时间步长进行了合理地控制.
1 计算模型
1.1 计算模型和网格划分
针对某滑行艇艇型模型,采用Maxsurf软件进行三维建模,导入Gambit软件进行网格划分.计算模型的网格划分采用分区混合网格系统,并在艇体附近进行网格加密,其中艇体附近的球形和正方体网格区域用于保证艇体纵摇、升沉运动时的网格质量.图1为计算模型及网格划分示意图,其中上部分为空气域,下部分为水域.水域为10L×4L×3L,空气域为10L×4L×1.5L(L为艇长).计算区域底部为固壁无滑移边界条件,左侧、上边界与两侧壁为速度入口,右边界为压力出口.滑行艇模型的主要参数见表1.

图1 三维模型计算控制区域及网格划分Fig.1 Calculation control zone and grid partition of the three-dimensional model

表1 滑行艇主尺度Table 1 Principal dimensions of planning boat
1.2 数值计算方法
采用三维非定常分离隐式求解器,利用VOF方法追踪自由液面,自由面重构格式采用Geo-Reconstruct格式,选用k-ε湍流模型,控制方程的扩散项采用中心差分格式离散,对流项采用二阶迎风格式;压力方程采用Body Force Weighted格式,压力速度合求解采用PISO算法,动网格采用弹性光顺法和局部重构,弹性常数参数设为默认值,局部重构算法中的最大网格扭曲率(maxim-um cell skewness)设为 0.85,Size Remesh Interval设为 5;启动Size Function函数,调整尺寸函数变化率β(size function rate)为1.5,控制边界处网格和内部网格的生长速度.
1.3 滑行艇运动预报算法
不计滑行艇的横荡、艏摇及横摇,在滑行艇纵向三自由度的基础上添加人工阻尼项,得到滑行艇的升沉、纵摇运动控制方程[7]如下:

式中:m为艇体的质量(kg);ω为艇体垂向速度(m·s-1);u为滑行艇前进速度(m·s-1);Z为艇体垂向合力(N);θ为纵摇角(rad);My为艇体纵摇力矩;Iy为艇体对y轴的转动惯量;Dh为垂荡人工阻尼系数,取0.1;Dp为纵摇人工阻尼系数,取0.1.
采用预测/修正的隐式方法求解运动方程,并通过求解滑行艇的运动控制方程预测线速度和角速度,然后采用三阶迎风格式进行修正:


判断计算结果是否收敛.若收敛则将艇体运动赋予网格系统[7],滑行艇运动响应预报算法流程如图2.

图2 滑行艇运动响应预报算法流程Fig.2 Flowchart for the respone prediction of planing
2 计算结果与分析
从水动力学的观点出发,若船舶的体积傅汝德数Fr2≥1.0,则属于高速船,其中包括高速排水型船舶和动力增升型船舶.对于1.0<Fr2<3.0航速区间的高速排水型船舶,在其支持力中起主要作用的是静浮力;而对于Fr2≥3.0的流体动力增升型船舶来说,其支持力起主要作用的是流体动升力.高速的流体作用于艇体表面,在水气交界面处产生剧烈的喷溅现象,喷溅对航行中高速船的影响不容忽视.
2.1 不同Fr2数下滑行艇的水动力性能
为了分析不同航速下滑行艇的水动力性能,选取与模型试验相同的计算工况,航速V=2,4,6,8,11 m·s-1,对应的体积傅汝德数 Fr2分别为 0.9,1.8,2.7,3.6,5.0.当 V=11 m·s-1时,滑行艇出现“海豚运动”,在此不作深入研究.
图3,4给出了滑行艇在不同航速下滑行艇阻力计算值与试验阻力的对比曲线和误差曲线,结果表明:在低航速时误差较小(10%左右),航速较高时误差较大(20%左右).出现这种现象的原因主要有:低航速时滑行艇处于排水航行状态,总阻力主要由摩擦阻力贡献,压差阻力贡献较小;高航速时情况恰好相反.由于滑行艇模型的转动惯量不能准确给定,引起滑行艇稳定时的纵倾角偏大,纵倾角的大小直接影响压差阻力,因此出现计算值大于试验值的现象.同时,由于计算机硬件条件的限制,艇体周围的网格划分不够密,单位网格覆盖艇体的面积过大,影响计算精度与准确性.
航速 V=2,4,6,8 m·s-1,4 种工况下滑行艇能够达到“动态平衡”状态.

图3 艇体阻力曲线Fig.3 Resisitance curves of vessel
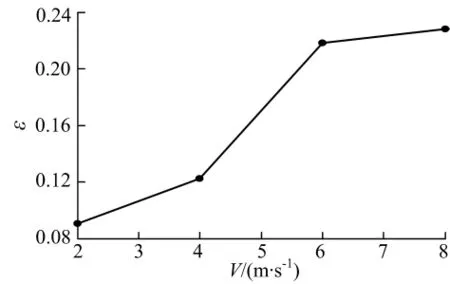
图4 滑行艇阻力误差曲线Fig.4 Resisitance error curves of vessel
图5给出了滑行艇在不同航速下的力矩变化曲线,低速航行时滑行艇处于排水航行状态,滑行艇纵倾角较小,艇体所受力矩较小;随着航速提升滑行艇由排水航行向滑行艇状态过渡,纵倾角变大,艇体所受力矩变大;滑行艇进入滑行状态后,随着航速进一步提升,滑行艇的纵倾角下降,艇体所受力矩出现下降.
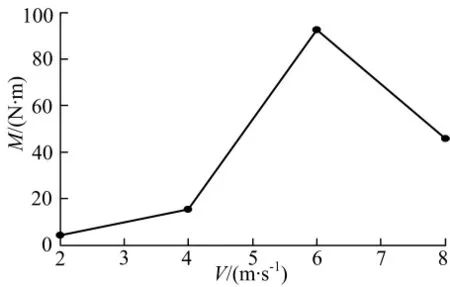
图5 滑行艇力矩曲线Fig.5 Moment curves of vessel
2.2 滑行艇的升沉纵摇运动特性分析
图6给出了滑行艇在不同航速下的滑行姿态的数值模拟结果.结果表明,滑行艇在航行过程中,在给定的主机输入功率下滑行艇将产生初始航速,并出现初始攻角,产生的升力将使艇体抬升到一定的高度,同时升力对艇体重心产生俯仰力矩,从而使滑行艇原来的平衡状态被打破.为达到新的动态平衡,艇体在不断变化的垂向力和力矩同时作用下产生升沉和纵摇运动,进而引起艇体的排水体积与浸湿面积同时发生变化,改变了滑行艇的航行阻力,从而使滑行艇的航速发生变化,而航速的变化又会引起滑行艇升力及力矩的变化.当滑行艇所受到的垂向合力与合力矩为零时,滑行艇的航行状态达到了动态平衡[6],滑行艇将保持这一姿态稳定航行,直到再次受到外界的干扰.文中的数值计算模型中,由于滑行艇的航行速度为定值,所以滑行艇最终趋于动态平衡.

图6 滑行艇不同航速下的滑行姿态Fig.6 Planning attribute of vessel at different speeds
图7,8 给出了航速 V=2,4,6,8,11 m·s-1时艇体重心位置的变化曲线和纵倾角变化曲线,反映了滑行艇升沉和纵摇运动的变化规律.从图7a),8a)可以看出,当 V=11 m·s-1时,艇体垂荡速度和纵摇角速度呈周期性变化,因此艇体升沉量和纵倾角也呈周期性变化,出现“海豚运动”现象,无法达到动态平衡.其他工况下,艇体垂荡速度和纵摇角速度趋于零,艇体升沉量和纵倾角趋于稳定值,趋于动态平衡.当滑行艇低航速时,出现下沉现象,当航速提高时,艇体抬升进入滑行状态.

图7 不同航速下滑行艇升沉变化特性Fig.7 Characteristics of heave at different speeds
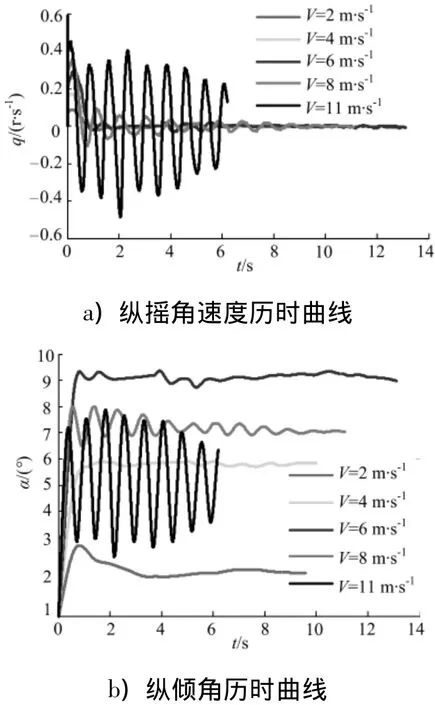
图8 不同航速下滑行艇纵摇变化特性Fig.8 Characteristics of pitch at different speeds
图9,10给出了不同航速下滑行艇航行达到稳定时升沉量和纵倾角计算值与试验值的对比曲线.升沉量与纵倾角的总体走势计算值与试验值一致;当V=2,8 m/s时误差较大,升沉量误差20%左右;当 V=4,6 m/s时误差较小,升沉量误差8.5%左右.滑行艇模型的转动惯量Iy直接影响艇体纵倾角,由于无法准确给定滑行艇模型的转动惯量,因此纵倾角误差较大,上文中提到的滑行艇总阻力随航速增加,计算误差增大的原因也在于此.滑行艇高速航行时,纵倾角对压差阻力的影响较大.
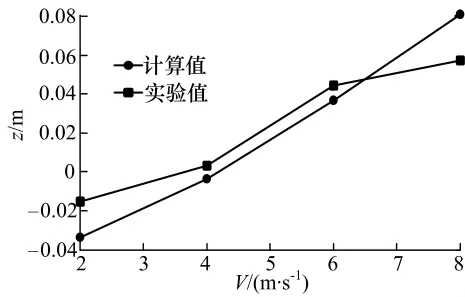
图9 升沉量曲线Fig.9 Curves of heave

图10 纵倾角曲线Fig.10 Curves of pitch
2.3 滑行艇艇底动压分布规律


图11 滑行艇艇底动压Fig.11 Dynamic pressure at bottom of vessel
2.4 滑行艇尾流场波高变化规律
均匀来流绕过滑行艇,由于滑行艇的存在流场发生相应的变化,图12给出了不同航速下滑行艇航行达到稳定时尾流场的波高云图.从图中可以看出,随着航速不断增加船体艏部抬出水面,水流从两侧流出,产生大量的飞溅和水花,尾流场波高不断增加,艇体尾缘“空穴”变大,形成“鸡尾流”,波峰后移.
3 结论
基于计算流体力学软件FLUENT,完成了滑行艇升沉纵摇运动的实时数值预报研究,主要得出如下结论:
1)转动惯量Iy对滑行艇运动响应数值预报的准确性具有至关重要的影响,滑行艇转动惯量Iy计算的经验公式有待修正;
2)基于计算流体力学软件FLUENT及运动网络技术,耦合求解滑行艇纵向运动预报程序,能够预报滑行艇的“海豚运动”现象.
艇底滑行面上的动压是艇体产生动升力的主要原因,图11给出了不同航速下滑行艇航行达到稳定状态时,艇底部动压分布云图.从图中可以看出,随着航速的增大艇底部动压值不断增大且动压力中心位置后移.

图12 滑行艇尾流场波高Fig.12 High of weak wave of vessel
References)
[1]Savitsky D,Brown P W.Procedures for hydrodynamic evaluation of planning hulls in smooth and rough water[J].Marine Technology,1976,13(4):381 -400.
[2]John M A.Resistance prediction of planing hulls:state of the art[J].Marine Technology,1993,30(4):296 -307.
[3]Nagai T,Yoshida Y.Estimation of resistance trim and draft of planing craft[J].Ship Technology Research,1993,40(3):133-137.
[4]邵世明,王云才.滑行艇阻力试验[R].上海:上海交通大学,1980.
[5] Panahi R,Jahanbakhsh E.Toward simulation of 3D nonlinear high-speed vessels motion[J].Ocean Engineering,2009,36:256 -265.
[6]Wilson R V,Carrica P M,Stern F.Unsteady RANS method for ship motions with application to roll for a surface combatant[J].Computers & Fluids,2006,35:501-524.
[7]Carrica P M,Wilson R V,Stern F.Unsteady RANS simulation of the ship forward speed diffraction problem[J].Computers & Fluids,2006,35:545 -570.
[8]Carrica P M,Wilson R V,Noack R W.Ship motions using single-phase level set with dynamic overset grids[J].Computers & Fluids,2007,36:1415 -1433.
[9]Ghassemi H,Kohansal A R.Higher order boundary element method applied to the hydrofoil beneath the free surface[C]∥Proceedings of the 28th International Conference on O-cean,Offshore and Engineering(OMAE2009).Honolulu,Hawaii USA:[s.n.],2009.
[10]王兆立,牛江龙,秦再白,等.基于CFD理论的滑行艇阻力数值计算[C]∥第十四届中国海洋(岸)工程学术讨论会论文集.内蒙古:[s.n.],2009,8:309 -315.
[11]高双,朱齐丹,李磊.基于神经网络的高速无人艇模糊PID 控制[J].系统仿真学报,2007,19(4):776 -779.
