水下爆炸载荷作用下加筋圆柱壳结构静动态协同优化设计

蔡威军，黄海燕

(江苏科技大学船舶与海洋工程学院，江苏镇江212003)

加筋圆柱壳结构是潜艇等水下结构物一种基本的结构形式，研究水下爆炸冲击波作用下加筋圆柱壳的毁伤效应对于潜艇等水下结构物的抗爆设计具有重要的意义.国内外学者在这方面做了大量的研究工作［1-6］.在结构的静力学性能(静水压力)约束下，优化设计可以使加筋圆柱壳结构的应力分布更加合理，从而实现结构质量的最小化.在结构的动力学性能(水下爆炸冲击波载荷)约束下，优化设计可以有效提高加筋圆柱壳结构的抗爆性能.在以往的研究中一般将静力学和动力学优化单独分开来研究，这样就无法准确反应水下爆炸冲击波载荷作用下加筋圆柱壳结构的实际工作状态.因此，论文基于协同优化算法和多岛遗传算法，建立了面向加筋圆柱壳结构的静动态协同优化的多学科优化模型，同时考虑结构对静力学、动力学响应的使用要求，对加筋圆柱壳结构进行静动态协同优化设计.

1 静动态协同优化模型及策略

协同优化算法(collaborative optimization，CO)是一种分布式的多级优化方法，将原有的设计优化问题分为一个系统级优化和多个学科级优化，通过将所有的耦合状态变量当作设计变量，解除学科间的耦合关系，使得各学科级优化可以独立并行实现［7］.

1.1 优化模型框架及策略

在协同优化的计算过程中，各学科级优化模型的设计变量在目标函数和约束条件的引导和限制下，朝着对本模型有利的方向变异，这就导致设计变量在不同的学科级优化模型中取值可能互不相同.为促使共享变量取值一致，各学科级模型必须作出一定的妥协和让步，即协同优化的系统级最优目标解一般都差于学科级独立优化得到的目标解.各学科级最优目标解将是协同优化追求的目标，总是希望协同优化目标解尽可能地接近学科级目标解，使两者之间的差异最小［8］.同时考虑静力学和动力学优化这两门学科的静动态协同优化的结构框架如图1.

图1 静动态协同优化模型架构Fig.1 Static and dynamic collaborative optimization framework

1.2 系统级优化

系统级优化模型的任务是使整个系统目标最优，并通过一致性约束条件来保证学科之间设计变量的一致性.系统级优化不仅独立地直接调用学科级分析工具，用于计算该学科的目标函数值，同时也调用学科级优化，以获取子学科级优化所获得的目标函数和设计变量的最优解［9-10］.为了消除各学科级目标函数值的量纲和数量级差异的影响，采用子学科目标函数的相对值构造系统级目标函数.在系统级优化模型中，为了避免出现无解或者收敛困难的情况，采用引入约束松弛因子［7］ε的方法来改造一致性约束条件.

在系统级优化中，以协调优化目标值和独立优化目标值之间差异最小化为目标函数，则系统级优化模型为:

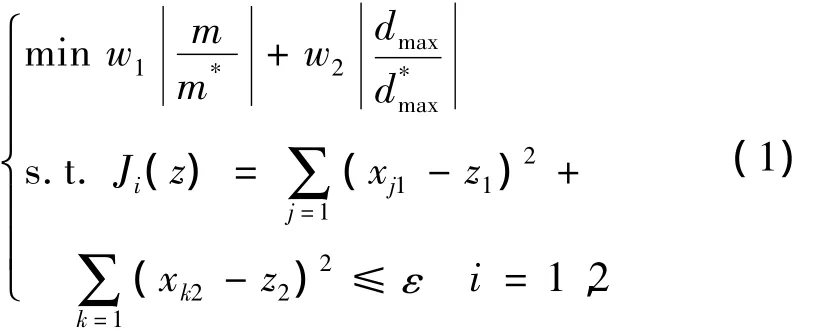
式中:wi为权重函数;m为系统级优化模型通过静力学分析得到的目标值;dmax为系统级优化模型通过动力学分析得到的目标值;m*为静力学优化模型得到的最优目标值;d*max为动力学优化模型得到的最优目标值;z={z1，z2}为系统级设计变量向量，其中z1为共享设计变量，z2为耦合设计变量;Ji(z)≤ε为子学科之间的一致性约束条件，用以保证学科之间状态变量的一致性;xj1为全局设计变量;xk2为状态设计变量.

1.3 学科级优化

学科级优化模型的任务是使本学科的目标最优.在学科级优化问题中，设计变量包括共享设计变量、学科之间的耦合状态变量以及只属于本学科的局部设计变量，约束条件只需满足本学科的约束条件.

1.3.1 静力学优化

在静力学学科级优化中，以静水压力作用下结构质量最小为目标函数，约束条件满足中国船级社CCS规范［11］中的许用应力约束要求，则静力学优化模型为:

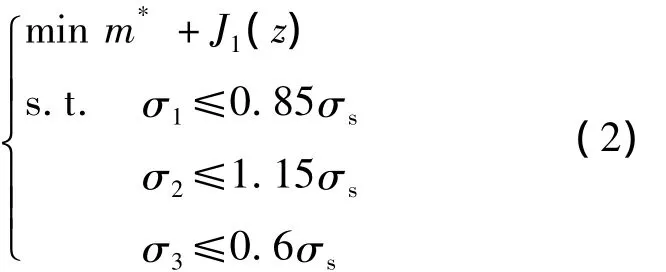
式中:m*为静力学优化模型得到的最优目标值;J1(z)为子学科之间的一致性约束条件;σ1为相邻肋骨中点处壳板的周向平均应力;σ2为肋骨处壳板的轴向应力;σ3为肋骨应力;σs为材料屈服强度.

1.3.2 动力学优化

在动力学学科级优化中，以水下爆炸冲击波载荷作用下结构的最大变形值最小为目标函数.我国军标中对安全半径的定义是指在水下爆炸时，使潜艇耐压壳体不产生塑性变形，潜艇耐压壳体距爆心的最近距离［12］.根据军标中安全半径的解析公式计算可得加筋圆柱壳的安全半径约为20 m.约束条件满足军标中安全半径和CCS规范中的许用应力要求，则动力学优化模型为:

1.4 协同优化策略

在系统级和学科级优化中，都选取多岛遗传算法［13］MIGA(multi-island genetic algorithm).用该方法通常能在整个设计空间中搜索到全局最优解.

多岛遗传算法是一种伪并行遗传算法，与传统遗传算法相比，多岛遗传算法将整个进化群体划分为若干子群体，称为“岛屿”，在每个岛屿上对子群体进行独立的选择、交叉、变异等遗传操作，定期在各个岛屿上随机选择一些个体进行“迁移”操作，将其转移到其它的岛屿上，通过这种方式维持群体的多样性，从而抑制早熟现象［14］.

2 算例分析

加筋圆柱壳尺寸为:半径r=3 m，舱长L=12 m，板壳厚 t=0.032 m;每隔 0.6 m 设置一个型环肋骨.材料的参数为:E=1.96 ×105MPa，ν =0.3，屈服极限 σs=800 MPa.下潜深度为500 m.200 kgTNT炸药位于加筋圆柱壳正下方水域中央，爆距R=22 m.

将水域和TNT炸药同时定义为多材料的三维欧拉体，在其相互覆盖部分的材料属性用分级来区别.将水单元的级别设定为1，两者相交部分即TNT的级别设定为2.壳体采用Langrange三角形和四边形单元来划分网格.为了简化建模过程，采用一般耦合方式，利用壳体本身构成的封闭面，将其定义为耦合面.水域采用与基本坐标系平行的Hex类型EULER单元，考虑到水域边界对爆炸冲击波的影响，在结构的上下侧水域取相同的水深，则水域的尺度为40 m×40 m×50 m.在水域的底部设为刚性，水域上端的边界设定开放压力为101 300 Pa，其他的边界设置为水介质可以流出的无反射边界，以避免爆炸冲击波在欧拉网格中产生积压，密度为1 000 kg/m3.圆柱壳的两端圆柱周上节点定义为简支.加筋圆柱壳结构和水域的有限元模型如图2.为了便于说明问题，图中只给出了四分之一水域模型，加筋圆柱壳位于有限元模型的中心，并被水域包围.

图2 有限元模型Fig.2 Finite element model

2.1 设计变量

选取板壳厚度和T型材的截面尺寸为设计变量，共计5个设计变量，如表1.

表1 优化前后不同优化方法下设计变量比较Table 1 Comparison of different algorithm between the initial and final design variablesmm

2.2 优化结果及分析

根据前面提出的静动态协同优化的多学科优化模型和优化策略，对加筋圆柱壳结构进行静动态协同优化分析.在学科级和系统级优化中，选取10个岛屿，每个岛屿由10个个体组成，岛屿内个体的交叉概率为0.9，变异率为0.01.每个设计变量用10位长的二进制数表示.各子种群的初始分布通过在可行域内的不同区域随机产生，这样更有利于得到全局最优解.设计变量的最优解如表1所示.

表2 优化前后不同优化方法下设计响应比较Table 2 Comparison of different algorithm between the initial and final design responses

表2给出了单学科和多学科协同优化方法得到的结构响应.三种方法在优化过程中所采用的设计变量、约束条件和优化算法及其参数都保持一致.在获得静力学优化时的设计变量和设计响应解后使用该设计变量值计算出结构的动力响应，也一并列入表2.同样在表2中给出动力学和多学科协同优化后相应的静力学、动力学响应计算值.优化前后迎爆面中心点加速度和结构最大变形值的比较如图3，4(图中a为加速度).

图3 优化前后迎爆面中心点加速度比较Fig.3 Comparison between the initial and final acceleration of central point toward explosion

图4 优化前后结构最大变形值比较Fig.4 Comparison between the initial and final largest deformation of the structure

从上述结果可以看出:

1)协同优化后，除T型腹板高有所增加外，其余设计变量的数值大小均有不同程度的减小，这说明加筋圆柱壳结构在初始设计时考虑了一定的裕度.

2)静力学优化获得了最轻的结构质量为56.2 t.但是在使用该学科设计变量最优解计算出来的结构动力响应中，结构的最大变形值由16.7mm上升到22.1mm，增加了32.3%;迎爆面中心点的加速度由 12.2 km/s2上升到 17.1 km/s2，增加了40.1%，从而降低了结构的抗爆性能.

3)动力学优化虽然使结构获得了最佳的抗爆性能(结构的最大变形值最小，仅为9.7mm)，但结构质量由65.5 t上升到70.2 t，增加了7.2%，这也导致了工程造价成倍增长.

4)静动态协同优化后，结构质量由65.5 t减少到59.2 t，降低了9.6%;同时结构的最大变形值由16.7mm 减少到14.4mm，降低了 13.8%.可见静动态协同优化后结构的主要力学性能指标得到了改善，既能够有效的降低结构质量，又能够有效的提高结构的抗爆性能，说明静动态协同优化后的结构在总体性能上要优于单学科优化后的结构总体性能，静动态协同优化的多学科优化模型能够有效改善结构的整体静、动力学性能.

3 结论

文中通过集成有限元分析软件和优化程序，建立了面向加筋圆柱壳结构的静动态协同优化的多学科优化模型;在静力学优化中，以结构质量最小为目标函数;在动力学优化中，以结构中的最大变形值最小化为目标函数;采用多岛遗传算法为优化算法，对加筋圆柱壳结构进行了静动态协同优化设计.结果表明:优化后加筋圆柱壳结构在一定程度上节省了工程原材料，大幅度降低了结构的动力响应，提高了结构的抗爆性能;同时，仍然满足强度和刚度要求，达到了预期目标.

References)

［1］Kwon Y W，Fox P K.Underwater shock response of a cylindrical subjected to a side-on explosion ［J］.Computers＆ Structures，1993，48(4):637-646.

［2］Hooker D T，Shin Y S.Damage response of submerged imperfect cylindrical structures to underwater explosion［J］.Computers＆ Structures，1996，60(5):683 -693.

［3］汪浩，程远胜，刘均，等.新型矩形蜂窝夹芯层加筋圆柱壳抗水下爆炸冲击载荷分析［J］.振动与冲击，2011，30(1):162-166.Wang Hao，Cheng Yuansheng，Liu Jun，et al.Anti-shock analysis for new type rectangular honeycomb sandwich stiffened cylindrical shells subjected to underwater explosion shock load［J］.Journal of Vibration and Shock，2011，30(1):162 -166.(in Chinese)

［4］袁建红，陈志坚.水下单壳体结构抗爆性能仿真分析［J］.舰船科学技术，2008，30(6):136 -139.Yuan Jianhong，Chen Zhijian.The anti-explosion simulation analyses on underwater single-shell structure［J］.Ship Science and Technology，2008，30(6):136 -139.(in Chinese)

［5］张阿漫，王诗平，汪玉，等.水下爆炸对舰船结构损伤特征研究综述［J］.中国舰船研究，2011，6(3):1 -6.Zhang Aman，Wang Shiping，Wang Yu.Advances in the research of characteristics of warship structural damage due to underwater explosion［J］.Chinese Journal of Ship Research，2011，6(3):1 -6.(in Chinese)

［6］徐永刚，宗智，李海涛.水下爆炸冲击波和气泡联合作用下结构响应数值分析［J］.中国舰船研究，2011，6(3):8-11.Xü Yonggang，Zhong Zhi，Li Haitao.Numerical analysis of structure response due to the combined effects of underwater explosion shock wave and bubble pulse［J］.Chinese Journal of Ship Research，2011，6(3):8 - 11.(in Chinese)

［7］Natallia M A，Robert M L.Analytical and computational aspects of collaborative optimization for multidisciplinary design［J］.AIAA Journal，2002，40(2):301 -309.

［8］Xue Caijun，Qiu Qingying，Feng Peien.Research on distributed collaborative optimization technology［C］∥Proceedings 2002 international symposium on distributed computing and applications to business.Wuxi Jiangsu，China:［s.n.］，2002:138 -143.

［9］黄海燕，林志祥，王德禹.船艉结构静动态多目标优化设计［J］.船舶力学，2011，15(11):1271 -1277.Huang Haiyan，Lin Zhixiang，Wang Deyu.Multi-objective optimization of ship stern under static and seismic loading［J］.Journal of Ship Mechanics，2011，15(11):1271 -1277.(in Chinese)

［10］黄海燕.船艉结构动力优化设计［J］.江苏科技大学学报:自然科学版，2012，26(2):114 -117.Huang Haiyan.Dynamic optimum design of ship sterns［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2012，26(2):114 -117.(in Chinese)

［11］中国船级社.潜水系统和潜水器入级与建造规范［S］.北京:人民交通出版社，1996.

［12］中国人民解放军总装备部.GJB4000-2000舰船通用规范［S］.北京:国防科工委军标出版发行部，2000.

［13］Hiroyasu T，Yoshida J，Sano M，et al.Distributed genetic algorithms ga2K specification［J］.Doshisha University，2002，25:130.

［14］潘治，李学斌.计及频率约束的潜艇环肋圆柱壳优化设计研究［J］.舰船科学技术，2009，3(3):21-24.Pan Zhi，Li Xuebin.Optimizaiton of ring-stiffened circular cylindrical shells with natural frequency constraints［J］.Ship Science and Technology，2009，3(3):21 -24.(in Chinese)