基于响应曲面法的大弯曲半径管材推弯回弹优化技术研究

李纯金，杜佐飞，章 威，褚月桥

(江苏科技大学机械工程学院，江苏镇江212003)

弯管零件因其具有优越的力学性能，多样的功用性以及易达到产品轻量化等方面的要求，已在许多工业领域得到广泛应用，尤其是在汽车输油管路、航空航天以及空调制冷管路等方面具有不可替代的作用［1］.但由于弯管零件是塑性加工成形，管子弯曲加工后，模具卸载必然会产生弯曲回弹，使得成形角和预先设定弯曲角存在偏差，造成弯曲质量下降和装配困难从而影响弯管件后续应用中的几何精度和形状精度，甚至造成大量材料报废.因此在特定弯管条件下，把弯管回弹角减少的越小越有利于产品的成形，越能实现良好的经济效益.

在实际生产中，弯管成形后产生的回弹角除了受自身几何参数的影响，更多的受模具等边界条件工艺参数的影响.因此对特定大小的弯管件，如何选择或控制其与模具的最优边界条件，对减少自身弯曲成形后回弹角具有重要的意义［2］.文中主要针对大弯曲半径(R/D＞3)管材在推弯成形后产生的回弹角，用响应曲面法算法对其进行优化，根据有限元模型模拟的结果，利用响应曲面法的优化计算最终算出一个最优边界条件，并通过优化拟合公式算出最优回弹角.

1 有限元建模

大弯曲半径管材在推弯时的三维有限元模型是在ABAQUS/Explicit软件平台上建立的，其有限元模型是根据江苏合丰机械有限公司生产的某型号的推弯机(图1)简化而来，有限元模型如图2.推弯成形过程的模具主要由轮模、推弯轮、压轮、导向轮、助推块、同步块以及芯棒组成.为了简化推弯模型，节省模型在有限元软件后处理过程中的计算时间，压轮、导向轮、轮模、芯棒、助推块和同步块等都定义为离散性刚体，管坯是可变形壳体，推轮是实体模型.

在推弯过程中，压轮的作用主要是压住管坯防止其沿纵向(Y轴方向)跳动和扭曲;导向轮的作用主要是起导向作用，即保证管坯在同步跟进和助推过程中沿着Z轴方向向前运动，而不发生Y轴方向的位移;轮模的作用主要是沿纵轴(Y轴)方向支撑管坯;推轮的作用是保证管坯弯曲成形;同步块和助推块都是给管坯提供位移或者速度;芯棒起管坯内部支撑作用，在整个推弯过程中保持固定不动.

图1 实际大弯曲半径推弯机模型Fig.1 Actual pushed bender model with big bend radius

图2 管材弯曲成形前后有限元模型Fig.2 Finite element model before and after tube bending

2 响应曲面法的设计思想

响应曲面法的基本思想是通过近似构造一个具有明确表达形式的多项式来表达隐式功能函数.本质上来说，响应曲面法是一套统计方法，用这种方法来寻找输入变量值的变异或其不确定性之后的最佳响应值.

响应曲面法如果存在许多因子，首先需要进行一个筛选试验以剔除不重要的因子.这可以通过诸如:分式析因设计(2k-p，3k-p设计)、Plackett-Burman设计以及非正规正交表等试验设计来实现.如果研究初始阶段的因子数已经比较少，就不必实施筛选试验.一般响应曲面法第1个阶段的主要目标是确定当前的试验条件或输入因子的水平是接近响应面的最优位置还是远离这一位置.当试验部位远离响应面的最优部位时，宜采用响应面的一阶逼近，使用一阶模型［3］:

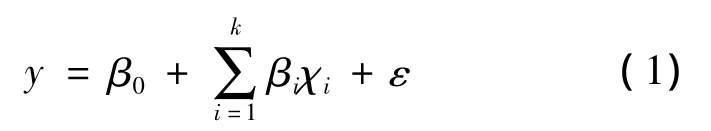
进行一阶设计估计出式(1)的系数.拟合一阶模型主要采用的是正交的一阶设计，正交的一阶设计包括了主效应不能互为别名的2k全因素设计和2k-p部分因素设计以及单纯形设计等.

在 χ1，χ2，…，χk的区域上采用最速下降法搜索以决定是继续进行一阶设计还是由于曲度的出现更换使用二阶设计.当试验区域接近最优区域或位于最优区域中时，进入第2阶段.这一阶段的主要目的是获得对响应面在最优值附近某个小范围内的一个精确逼近并识别出最优过程条件.在响应面的最优点附近，曲度效应是主导项，用二阶模型来逼近响应面［3］:

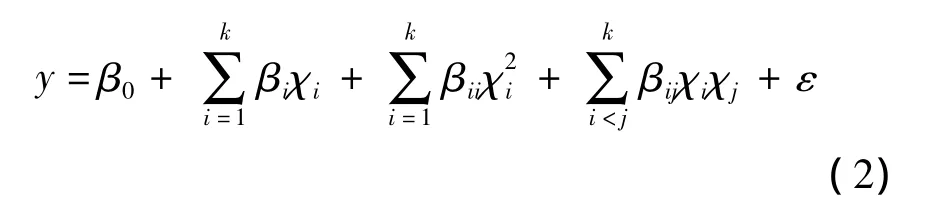
式中:β为变量系数，βi为一阶系数，βij为二阶系数.

进行二阶设计估计出式(2)的系数.

二阶设计有很多种，中心复合设计(Central Composite Design，CCD)和 Box-Behnken设计(BBD)是经典的二阶设计.目前，CCD应用最为广泛，这是因为CCD具有一些良好的性质:① 恰当地选择CCD的轴点坐标可以使CCD是可旋转设计，为设计在各个方向上提供等精确度的估计;②恰当地选择CCD的中心点试验次数可以使CCD是正交的或者是一致精度的设计，然后进一步确定最优点的位置［4-5］.

文中在研究影响大弯曲半径管材推弯回弹因素的优化时，主要考虑了在定性材料时2种不同接触面间的摩擦系数、助推块助推速度及模具间隙这几种因素的影响，因此选择研究的因子数较少，实施筛选试验较为简便.而且在响应面的最优点附近，曲面响应是主导项，需用二阶模型进行进一步优化出确定点以便于代入有限元模型进行计算，所以采用的是二阶设计，基于CCD设计的以上优点［6］，主要采用基于CCD的二阶设计.

3 优化方案实现

3.1 优化方法流程图

基于响应曲面法进行优化时，首先要确定对目标函数有影响的约束变量、约束条件和预定的目标函数优化值，然后代入响应曲面程序，进行多次迭代计算，最后得出最优解［7］.文中基于响应曲面法对大弯曲半径管材推弯成形后回弹角优化的具体流程如图3.

图3 优化流程图Fig.3 Flow chart of optimization

从图3中可以看出，首先要确定影响大弯曲半径管材推弯成形后产生回弹角的因素，并对其进行单独编号，这些因素被定义为优化目标函数的约束变量，然后将这些参数(约束变量)写入csv文件(执行算法的一种文件)并代入优化程序，经过响应曲面法对这些参数进行初步分配后，得到一些列重组变量;其次利用ABAQUS软件将这些重组的变量代入有限元模型，进行运行计算并在后处理软件中测出各组数据的回弹角和此时截面壁厚变化值(在考虑回弹角的情况下，要确保弯管件管坯的质量，使管坯推弯成形后回弹角减小到最小的同时，管坯的质量也达到设计要求);第3步把从有限元模型运行后测到的数据、优化所必须具备的约束条件及理想中得到的实验回弹角一起写入原先的csv文件;第4步将更新后的算法文件再次代入优化程序，经过响应曲面法的计算，得到最优数学计算模型即拟合方程和最终的优化目标函数值.

3.2 优化步骤及结果

文中研究对象是弹塑性比较好的铝合金管(3003)，其中铝合金管的弹性模量E=70 000 MP，密度 ρ=2.7 ×103kg/m3，泊松比γ =0.33，材料选择的本构模型是指数硬化模型:σ=Κ(εο+ε)n(其中，K是材料硬化系数，n是材料硬化指数，εο是材料常数［8］.)

对大弯曲半径管材在推弯角为0.75 rad时进行优化分析，具体的优化步骤如下.

1)选取对大弯曲半径推弯成形后回弹角有影响的约束变量，分别为:推轮对管坯的摩擦系数u，轮模、压轮、导向轮对管坯的摩擦系数u1，同步块对管坯的助推速度v以及模具与管坯的间隙Δt.具体参数如下:

u=(0.05～0.25)mm u1=(0～0.1)mm

v=(119～146)mm/s Δt=(0.25～0.625)mm

2)选取此次优化约束条件:管坯推弯成形后截面壁厚值t′;选取截面壁厚值t′是为了管坯推弯成形后管坯的质量得到保证.选取的管坯推弯前壁厚t为2mm.

t′=(2～2.2)mm

3)选取目标函数为回弹角y，设定大弯曲半径管材在推轮推弯角为0.75 rad时，回弹角为4°左右.其中所选截面壁厚值和回弹角是下步优化程序中得到的27组随机重组变量经有限元计算后所得数值的平均值.

4)将上述约束变量u、u1、v和Δt代入优化程序得到27组随机重组变量，将这27组变量分别带入到ABAQUS软件中，对其进行有限元建模并运行计算，在后处理软件中测出相应的回弹角和截面管壁增厚值.具体数值如表1.

表1 约束分组变量及测量值Table 1 Constraint grouping variable and measured values

5)更新csv文件，分别写入27组重组变量数据，并将有限元处理后测的管壁增厚值和相应的回弹角值以及约束条件和理想的目标函数值都写入csv文件，并更换csv文件操作类型.

6)将csv文件再次代入优化程序，经过多次计算(对0.75 rad时共进行了20步参数计算选取)后，算法自身根据约束变量参数得出的拟合方程(优化数学模型)如式(3，4)所示，以及得出最优回弹角情况下的约束变量的参数.

截面壁厚变化优化拟合数学公式如式(3)

回弹角优化拟合数学公式如式(4)

经过多步迭代计算，最终得出的最优约束变量参数如下:u=0.050 001，u1=0.000 132，v=130.464 2，Δt=0.526 652.

3.3 优化结果检测

在上节中，设定的目标函数理想最优回弹角和截面壁厚增加值是取上步27组优化数据经有限元计算后测出的回弹角和截面壁厚增加值的平均值，所以回弹角取的是4°，截面壁厚增加后的值是2.2mm(其实际优化结果理论应小于或等于2.2mm).经过响应曲面法多次计算后得到一组影响回弹角参数的最优解，其优化后得出的最优解是:回弹角为4°，截面壁厚值t′为2.199 801mm.对比理论平均值和优化后的两组数值可以看出:优化后回弹角与理论平均值的回弹角相等，截面壁厚增厚率略小于理论平均值的壁厚增厚率数值，因此本优化方法满足理论优化要求.

利用上步优化拟合数学模型，将多次计算后得出的最优参数值重新代入ABAQUS软件中进行建模和运行，并在后处理过程中测出实际所得回弹角和截面壁厚增加值，其值分别是:回弹角为4.07°，截面壁厚值为2.209mm，因其误差值太小(回弹角的误差值为1.75%，截面壁厚误差值接近0.41%)，因此基于响应曲面法对回弹角的优化是满足精度要求的.

同理分别经响应曲面法算得大弯曲半径管材在推轮推弯角 α 为 0.25，0.35，0.45，0.55，0.65，0.85 rad时影响回弹角因素的最优参数值如表2，并将优化后参数代入有限元软件测得实际回弹角，将实测回弹角和优化理论回弹角绘制成曲线如图4，从图中可以看出实测回弹角和优化理论回弹角尽管有稍微的波动偏差，但它们的大小几乎是一致的，呈小幅度的上下波动趋势，误差值(最大误差＜10%)较小，在可控范围内.

对于产生的误差原因可能是:优化得到的最优参数值在代入有限元软件时，有限元自身局限性会将有些约束变量数据的后几位省略或进位，导致实际优化参数与有限元参数有误差存在.优化前实测回弹角与优化后实测回弹角如图5.

表2 最优约束参数值Table 2 Optimal constrained parameters

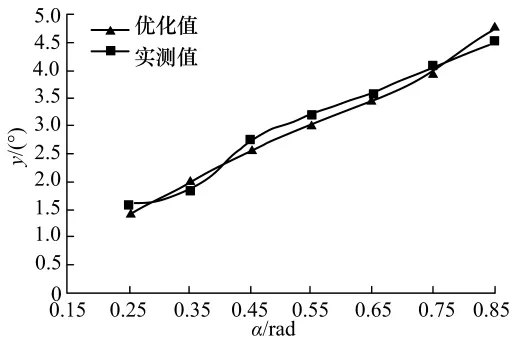
图4 回弹角优化值与优化后实测值比较Fig.4 Optimization and after-optimization measured values of rebound angle

从图5可以看出，大弯曲半径管材推弯成形后，在没有经过优化前实测的铝合金管的回弹角明显大于优化后实测的铝合金管的回弹角，因此基于响应曲面法对大弯曲半径管材推弯成形后回弹角的减小具有实际意义和应用价值.

图5 优化前后实测回弹角比较Fig.5 Measured rebound angles before and after optimization

4 结论

利用abaqus软件对大弯曲半径管材推弯过程进行建模，并基于响应曲面法对大弯曲半径管材(铝合金管)推弯成形后的回弹角进行优化.着重从推轮与管坯间的摩擦系数、轮模、导向轮、压轮与管坯间的摩擦系数、模具与管坯间隙及助推块的助推速度这4种因素对大弯曲半径管材推弯回弹进行优化，得到推轮推弯角为0.75 rad时最优参数下的最小回弹角，并得出在推弯角不同时的最优参数下的最小回弹角，同时得出了铝合金管在优化前后回弹角的实测曲线图.通过曲线图的比较分析，可以知道将优化后的参数重新代入有限元模型进行运算，测得的回弹角明显小于未经优化时的回弹角.因此，基于响应曲面法的优化方法在管坯弯曲质量得以保证的前提下可以得出最优回弹角，为弯管的回弹提供了一种新的优化方法.

References)

［1］杨合，孙志超，林艳，等.面向21世纪的先进塑性加工技术与管成形研究发展［J］.塑性工程学报，2001，8(2):86-88.Yang He，Sun Zhichao，Lin Yan，et al.Research and development of advanced plastic processing technologies and tube forming for the 21st century［J］.Journal of Plasticity Engineering，2001，8(2):86-88.(in Chinese)

［2］Lou H Z，Steison K A.Three dimension tube geometrycontrol for rotary draw tube bending partl:bendangle and overall tube geometry control［J］.Journal of Manufacturing Science and Engineering，2007，123(5):258-264.

［3］王永菲，王成国.响应面法的理论与应用［J］.中央民族大学学报，2005，8(14):236-237.Wang Yongfei，Wang Chengguo.The application of response surface methodology［J］.Journal of the Central U-niversity For Nationalties，2005，8(14):236-237.(in Chinese)

［4］汪仁官.试验设计与分析［M］.北京:中国统计出版社，1998:23-35.

［5］Myers R H.Response surface methodology 2 current status and future directions［J］.Journal of Quality Technology，1999，(1):31-32.

［6］张润楚，郑海涛，兰燕.试验设计与分析及参数优化［M］.北京:中国统计出版社，2003:65-72.

［7］贺连芳，赵国群，李辉平，等.基于响应曲面方法的热冲压硼钢B1500HS淬火工艺参数优化［J］.机械工程学报，2011，47(8):77-82.He Lianfang，Zhao Guoqun，Li Huiping，et al.Optimization ofas quenching parameters for hot stamping boron steel B1500HS based on response surface methodology［J］.Journal of Mechanical Engineering，2011，47(8):77-82.(in Chinese)

［8］张旭光.数控弯管回弹的解析-数值模拟研究［D］.陕西西安:西北工业大学，2003:41-48.