溃坝自由表面流动的移动粒子半隐式法模拟

刘永涛，朱仁庆

(江苏科技大学船舶与海洋工程学院，江苏镇江212003)

自从文献［1］于1996年首先提出MPS(moving particle semi-implicit，MPS)方法以来，作为一种擅长于处理自由表面大变形问题的无网格粒子法，该方法获得了快速发展，并在众多流动问题模拟中获得了广泛应用，例如溃坝［2-5］、波面破碎［6-7］、波浪中浮体运动［8］、甲板上浪［9-10］、液舱晃荡［10-12］等问题.文中针对溃坝问题，采用MPS方法进行二维自由表面大变形现象的数值模拟与验证.

1 液体流动的数学模型

考虑不可压缩粘性流体假设，则液体运动的控制方程为:

连续方程

动量输运方程

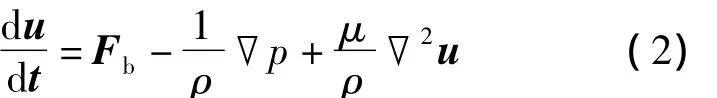
式中:μ为流体动力粘性系数;Fb为质量力;u为流速;ρ为流体密度;p为压强.

2 MPS计算模型

2.1 核函数选取

采用MPS法对计算流场进行粒子离散化后，流体粒子就拥有位置、速度、质量和压力这些物理量，而且在模拟过程中，流体粒子将和周围粒子产生相互作用并交换物理量.通常将流体粒子间的这种相互作用限定于影响半径范围内，并通过定义核函数w(r)来描述该范围内粒子相互作用的变化规律.文中所采用的核函数为:

式中:re为影响半径，文中取re=3.2l0，l0为初始相邻粒子间距.

2.2 粒子密度计算

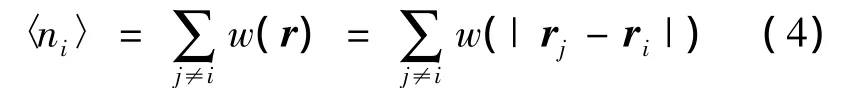
MPS法模拟过程中，随着流体粒子的不断移动将可能引起流体密度的变化.这种流体密度的变化通过定义某一粒子i影响域内相邻粒子的密集程度，即粒子数密度ni来实现.因此，在ri处的粒子i的粒子数密度为:

式中:rj为周围粒子j的瞬时位置.因此对不可压流体，这意味着计算过程中流体的粒子数密度ni需要保持为初始粒子密度常数n0.

2.3 梯度算子模型

由于动量输运方程中存在物理量的梯度项，因此定义梯度算子计算模型.考虑物理量φ，对于某相邻的两个粒子i和j，它们之间梯度矢量可表示为两者物理量差值与对应矢量半径之比:

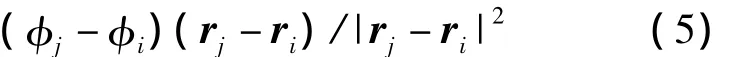
则在粒子i的影响域内物理量φ的梯度即为周围物理量梯度的加权平均:式中:d为流场的空间维数.

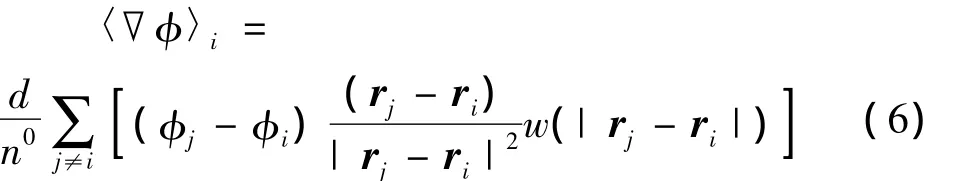
2.4 Laplace算子模型

对于动量输运方程中物理量的Laplace算子项，采用文献［3］所给出的公式:式中系数λ为:

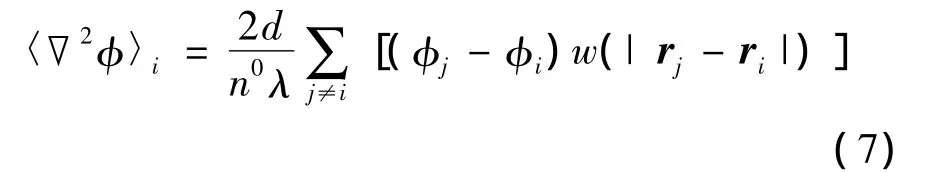
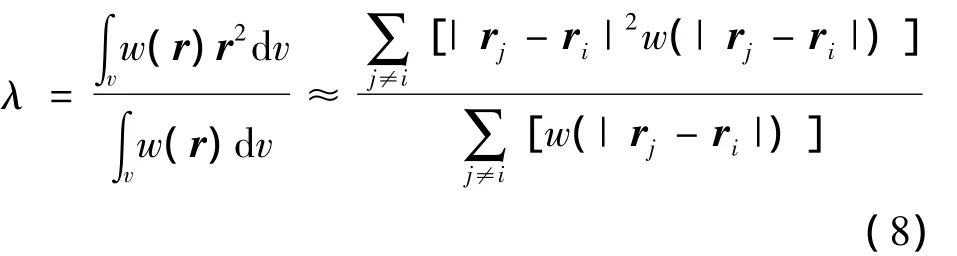
2.5 控制方程的数值解法

在每一个时间步Δt，MPS法采用分步方法来求解动量方程.

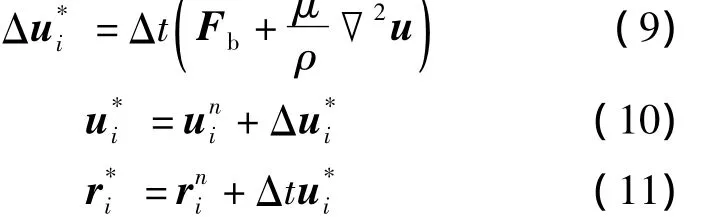
1)考虑动量方程中质量力项以及粘性力项，显式计算粒子i的速度变化量Δu*i以及临时速度和临时位置为:2)计算该瞬时位于临时位置r*i的粒子数密度n*.由于在一般情况下，n*不等于初始粒子数密度n0，为满足流体不可压条件，因此将其修正到n0.该修正过程通过定义粒子数密度n*的修正值n′来实现.

3)求解压力Poisson方程得到压力Pn+1.该方程由考虑动量方程压力梯度项得到的速度修正量u′和粒子数密度修正值n′之间关系建立.

首先只考虑动量方程中压力梯度项，可得速度修正量 u′:

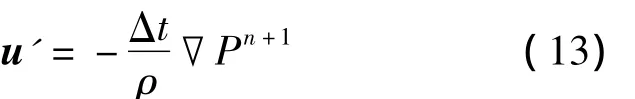
再根据连续方程，粒子数密度修正值n′与速度修正值u′需要满足如下关系式:

应用迭代方法求解该Laplace方程，计算得到压力场Pn+1.

4)将新压力场Pn+1代入式(13)计算u′，再次修正得到新时刻速度场uni+1和粒子位置rni+1.

由上述两式可得到压力Poisson方程:

2.6 自由表面判别

根据粒子数密度定义可知，自由表面处的流体粒子数密度会小于内部流体粒子数密度.因此，前述MPS法分步计算过程第2)步中，若根据式(12)得到的临时粒子，数密度n*i＜βn0，则判别其为自由表面粒子并设定压力为零，此处根据文献［13］取 β 为0.97.

2.7 固体边界条件

在固体边界上设置一层边界粒子来防止流体粒子穿越固体边界.由于靠近边界处粒子数密度将会小于内部流体粒子数密度，并被误判为自由表面粒子，为此，在固体边界外部另外平行布置若干层位置固定的虚拟粒子［2］，文中取为3层，具体布置如图1，该类粒子仅参与局部粒子数密度计算，而不参与压强和流速计算.

图1 边界处粒子布置示意图Fig.1 Schematic view of the layout of boundary particles

3 算例

3.1 溃坝模拟1

流动域尺寸:长 L=0.8 m，高度 H=0.6 m，初始静止水柱长度 a=0.175 m，高度h=0.35 m，被挡板限制于流域左侧.当挡板打开后，水柱将在重力作用下向右侧流动，并在不同时刻流经底板的不同水平位置处，到达右壁面后在惯性作用下继续沿壁面上冲.为研究粒子直径对计算结果的影响，取粒子直径 l0分别为0.004，0.006，0.008 m.

图2 自由表面的试验结果［14］与数值模拟结果对比Fig.2 Comparison of free surface configurations between experimental results and numerical results

图3 波面流经底板水平位置的模拟结果对比Fig.3 Comparison of numerical results for the water front positions along the tank bottom

图4 波面流经底板水平位置的试验以及模拟结果(l0=0.004 m)对比Fig.4 Experimental and numerical results(l0=0.004 m)for the water front positions along the tank bottom

对上述溃坝过程的考察，主要关注各瞬时的自由表面大变形特征，相关对应结果可用图2～4表示.图2为瞬时自由表面结果，显示了在不同时刻自由表面的数值模拟结果(右图，对比3种粒子直径流动模拟结果可知较小粒子直径对复杂局部流动能有较精细地刻画，本处仅提供粒子直径等于0.004 m 的计算结果)与试验结果(左图，Hu［14］的试验)的对比情况.从4个典型时刻的对比图可以看出，自由表面的数值模拟结果与试验结果较为一致.图3为3种不同粒子直径条件下不同时刻底板处波面水平位置的数值模拟对比，可见随着粒子直径减小，数值模拟结果趋于稳定，文献［4］也有类似结论.因此，选取较小的流体粒子直径会有较好的计算结果，但压力Poisson方程的求解也更耗时.综合权衡计算耗时以及数值模拟精度，文中选取相对较小的粒子直径.图4为波面时历结果，显示了在不同时刻运动波面流经底板水平位置时的对比，可见 MPS 模拟结果(l0=0.004 m)与 Hu［14］的试验结果在无量纲时刻小于2.0时吻合较好，在这之后两者略有分离，并且MPS模拟结果略大于试验结果.

3.2 溃坝模拟2

流动域尺寸:长 L=0.584 m，高度 H=0.438 m;初始静止水柱长度a=0.146 m，高度h=0.292 m，位于流动域左侧.在距离左壁面0.292 m的底板处固定一方形木块，其长度为0.024 m，高度为0.048 m.当挡板打开后，水柱向右侧流动并经过木块位置处，波面破碎后继续冲向右壁面.为较精确细致地反映波面流经木块后的破碎变形状况，本算例选取粒子直径为较小值，即l0=0.002 m，流动域共计有流体粒子10 658个，边界粒子1 022个，边界外三层虚拟粒子3 102个.

图5 自由表面的试验结果［15-16］与数值模拟结果对比Fig.5 Comparison of free surface configurations betweenexperimental results［15 -16］ and numerical results

在本算例中，由于水柱流经方木块受阻并产生剧烈冲击后，沿木块顶部快速跃起形成舌状，此后部分流体在惯性作用下继续向右冲击右壁面，其余部分受重力作用下落并冲击底板.该过程中自由表面产生显著的破碎、翻卷、合并、冲顶等典型的大变形运动(图5).对上述过程的真实有效模拟是重点也是难点.在图5中，从0.1～0.5s4个不同时刻，对比自由表面的数值模拟结果(右图)与试验结果［15-16］(左图)可以看出，0.1～0.3s各瞬时大变形自由表面的MPS数值模拟效果较为真实，仅在0.5s时刻两者有明显差别，表现在试验结果中流动域右下侧出现大体积气体卷入现象，而模拟结果流体下落并堆积于右下侧，同时由于粒子法本身原因出现大量散落的流体粒子.

4 结论

针对两种溃坝问题，文中应用MPS法对自由表面大变形现象进行了数值模拟，对比分析了不同粒子直径大小对数值模拟结果的影响，并与试验结果进行了对比验证.结果表明:选取较小粒子直径有助于较精细地模拟大变形局部流动现象，且提高模拟计算结果的稳定性;MPS方法对翻卷、破碎、冲顶等自由表面大变形问题具有优势，模拟效果较好.

References)

［1］Koshizuka S，Oka Y.Moving-particle semi-implicit method for fragmentation of incompressible fluid［J］.Nuclear Science and Engineering，1996，123(3):421 -434.

［2］Koshizuka S，Tamako H，Oka Y.A particle method for incompressible viscous flow with fluid fragmentation［J］.Computational Fluid Dynamics Journal，1995，4(1):29 -46.

［3］Shakibaeinia A，Jin Y C.A weakly compressible MPS method for modeling of open-boundary free-surface flow［J］.International Journal for Numerical Methods in Fluids，2010，63(10):1208 -1232.

［4］徐刚，段文洋.自由面流动模拟的MPS算法研究［J］.哈尔滨工程大学学报，2008，29(6):539-543.Xu Gang，Duan Wenyang.An investigation of MPS algorithm for free surface flow simulation［J］.Journal of Harbin Engineering University，2008，29(6):539 -543.(in Chinese)

［5］张雨新，万德成.用MPS方法数值模拟低充水液舱的晃荡［J］.水动力学研究与进展，2012，27(1):100-107.Zhang Yuxin，Wan Decheng.Numerical simulation of liq-uid sloshing in low-filling tank by MPS［J］.Chinese Journal of Hydrodynamics，2012，27(1):100 -107.

［6］ Koshizuka S，Nobe A，Oka Y.Numerical analysis of breaking waves using the moving particle semi-implicit method［J］.International Journal for Numerical Methods in Fluids，1998，26(7):751 -769.

［7］Gotoh H，Sakai T.Key issues in the particle method for computation of wave breaking［J］.Coastal Engineering，2006，53(2):171 -179.

［8］Shibata K，Koshizuka S，Sakai M，et al.Lagrangian simulations of ship-wave interactions in rough seas［J］.O-cean Engineering，2012，42:13 -25.

［9］Shibata K，Koshizuka S.Numerical analysis of shipping water impact on a deck using a particle method［J］.O-cean Engineering，2007，34(9):585 -593.

［10］Shibata K，Koshizuka S，Tanizawa K.Three-dimensional numerical analysis of shipping water onto a moving ship using a particle method［J］.Journal of Marine Science and Technology，2009，14(2):214 -227.

［11］Pan Xujie，Zhang Huaixin，Lu Yuntao.Numerical simulation of viscous liquid sloshing by moving-particle semiimplicit method［J］.Journal of Marine Science and Application，2008，7(3):184 -189.

［12］龚少军，姚震球.基于粒子法的液舱共振晃荡现象研究［J］.江苏科技大学学报:自然科学版，2010，24(6):534-538.Gong Shaojun，Yao Zhenqiu.Study on resonance sloshing by particle method［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2010，24(6):534 -538.(in Chinese)

［13］Khayyer A，Gotoh H.Enhancement of stability and accuracy of the moving particle semi-implicit method［J］.Journal of Computational Physics，2011，230(8):3093 -3118.

［14］Hu Changhong，Sueyoshi M.Numerical simulation and experiment on dam break problem［J］.Journal of Marine Science and Application，2010，9(2):109 -114.

［15］Martin J C，Moyce W J.An experimental study of the collapse of liquid columns on a rigid horizontal plane［J］.R Soc，1952，244(882):312 -324.

［16］Koshizuka S，Oka Y，Tamako H.A particle method for calculating splashing of incompressible viscous fluid［C］∥In:Proceedings of the International Conference，Mathematics and Computations，Reactor Physics，and Environmental Analyses.Washington，USA:American Nuclear Society，1995:1514-1521.