战术导弹三回路过载驾驶仪时频特性分析

2013-02-28王嘉鑫林德福祁载康

兵工学报 2013年7期

王嘉鑫，林德福，祁载康

(北京理工大学宇航学院，北京100081)

0 引言

在未来空战中，近程空对空格斗导弹应具备越肩发射攻击第4 代战斗机的能力，从而对导弹控制系统提出了3 点新要求:1)亚秒级的制导时间要求系统快速响应;2)对抗高机动目标强调对静不稳定弹体的增稳能力;3)大空域飞行要求系统具备强鲁棒性。三回路过载驾驶仪能够适应上述需求，其过载主反馈保证了快速性;增稳回路利用“合成稳定性”和高频振荡环节设计解决了对静不稳定弹体的控制问题，同时增强了系统的鲁棒性[1－7]。

现有文献大多关注在给定性能指标下三回路过载驾驶仪的设计方法，而研究该类驾驶仪时频特性的资料较少。Nesline 等[5]认为三回路过载驾驶仪对飞行高度、速度以及弹体质心变化的敏感度较低，鲁棒性较强，并可降低雷达天线罩斜率寄生回路对制导系统的影响。文献[8 －11]提出了通过包含时域响应和高频性能的混合指标、ITAE 最优控制指标和改进的Butterworth 滤波器等方法设计驾驶仪性能指标，并提出了基于输出反馈极点配置的工程设计方法。

本文对三回路过载驾驶仪及其内回路的结构、时域和频域性能以及对静不稳定弹体的增稳能力进行了解析分析，并通过无量纲分析方法，提出了一种三回路过载驾驶仪的设计思路。

1 弹体控制模型

将弹体视为刚体模型，利用小扰动线性化假设方法，建立去耦的纵向弹体控制模型，可由如下微分方程表示:

推导由舵转角到弹体角速度以及法向过载的传递函数分别为

式中:Tm和ξm分别为开环弹体的时间常数和阻尼系数;Tα为攻角滞后时间常数;A1和A2为包含舵面升力的高频环节系数和ka分别为前向增益。表1 给出了弹体参数的物理意义与表达式[7]，其中:Jz为弹体俯仰轴的转动惯量，S 和L 分别为特征面积和特征长度分别为俯仰力矩系数导数，为升力系数导数。对静稳定弹体有aα＞0，且aα越大静稳定度越高;aα＜0 表示静不稳定;aα=0 为静中立稳定。同时对正常式布局弹体aδ＞0，而对鸭式布局弹体aδ＜0.本文采用的典型弹体仿真参数如表2[10]所示。

表1 弹体参数的物理意义和表达式Tab.1 Physical significance and expressions of coefficients

表2 仿真参数Tab.2 Simulation parameters

2 新弹体分析

作为多回路反馈的高阶控制系统，三回路过载驾驶仪由内向外包括开环弹体以及姿态角速度、姿态角和加速度3 条反馈控制通道，把上述3 条反馈回路独立构成的飞行控制系统分别简称为阻尼回路新弹体、增稳回路新弹体和三回路驾驶仪。

2.1 开环控制系统

开环控制系统也称开环弹体，如图1 所示。假设舵机控制系统较快，忽略其动力学滞后，kACT为舵机增益，正常式气动布局弹体取kACT= －1，鸭式布局kACT=1，则系统传递函数为

式中:KC0=kACTvkϑ·为前向增益;k0为增益调整系数。(4)式表明开环控制系统受弹体气动性能和飞行环境的影响较大，鲁棒性较差，且通常为极度欠阻尼系统，ξm约为0.1[10]，弹体频率较高，抗干扰能力较弱，不能控制静不稳定弹体，因此，工程上常常需要设计控制器改善开环弹体的性能。

图1 开环控制系统Fig.1 Open loop control system

2.2 阻尼回路新弹体

阻尼回路新弹体是在开环弹体的基础上，通过姿态角速度反馈构成的控制系统，其结构如图2 所示，传递函数为

式中:KC1=(kACTkϑ·v)/(1 +kACTkg为闭环增益;为时间常数;ξ1= (2μmTm+为阻尼;k1为增益调整系数;kg为设计参数，当kgkϑ·≪1 时，有KC1≈kACTkϑ·v;T1≈Tm，ξ1≈μm+ |kgkϑ·Tα|/2Tm，通过设计kg使系统(5)式具有良好的阻尼系数，而新弹体的快速性和静稳定性与开环弹体近似，且系统增益易受弹体飞行状态的影响，鲁棒性较低。新弹体的开环幅值穿越频率ωCR可由(6)式近似计算[5]:

若要求新弹体稳定，需满足不等式组

将(8)式代入(6)式，得到ωCR＞|aα|/bα.

分析表明，1)对静稳定弹体，不等式(8)式始终成立，而对静不稳定弹体，控制系统的稳定性与平衡状态下攻角和舵转角的传递比的倒数|aα/aδ|相关，当舵效率较高时，即|aα/aδ|较小，阻尼回路新弹体更易达到稳定;2)开环增益kgkϑ·对系统的稳定性影响较大，但(6)式表明ωCR与kg呈正比，而考虑工程上为获得足够的稳定裕度通常期望ωCR远小于舵机频带或传感器频带，因此阻尼回路对静不稳定弹体的增稳性能将受到频带限制。

2.3 增稳回路新弹体

增稳回路新弹体是在阻尼回路的基础上，增加姿态角主反馈构成的控制系统，如图3 所示。

图3 增稳回路新弹体Fig.3 Stabilizing loop system

增稳回路的设计目的是在弹体响应的短周期内以姿态角速率的积分近似攻角，并将与攻角呈正比的恢复力矩信号反馈至输入端，从而增加了弹体的静稳定性，且这种增稳能力取决于控制系统的设计参数，因此可以被称为“合成稳定性”。在工程上，对姿态角的测量较为容易，因此增稳回路普遍采用姿态角作为主反馈量。(10)式给出了增稳回路新弹体的传递函数:

对比(10)式和(11)式可知，增稳回路新弹体与姿态驾驶仪具有相同的特征方程:

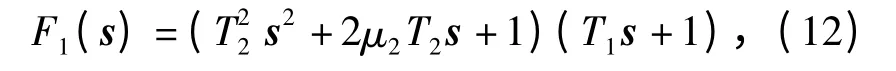
式中:T1和T2分别为一阶和二阶环节时间常数;μ2为阻尼系数。由姿态驾驶仪性能可知，当μ2≈0.5 时，存在如下关系[12]:T1＞Tα，T2＜Tm，即增稳回路新弹体的二阶环节时间常数小于开环弹体时间常数Tm，从而使新弹体的振荡频率加快，由于静稳定性与弹体无阻尼振荡频率呈正比，增稳回路新弹体的稳定性较开环弹体有所提高;同时一阶环节时间常数大于攻角滞后时间常数Tα，导致系统的响应速度很慢，并且由T1决定的一阶根为主导极点，而通常又有Tα≫Tm，因此系统闭环极点间的“距离”由此拉开。

若要求增稳回路新弹体稳定，需满足下列不等式组:

解得

可知当增稳回路和阻尼回路新弹体达到临界稳定时分别所需设计增益kgSL和kgDL的比为

(15)式表明，提高弹体静稳定性至临界稳定时，增稳回路新弹体所需设计增益kg远小于阻尼回路新弹体，而增稳回路的开环穿越频率ωCR仍可由(6)式近似计算[5]，那么当kg下降后ωCR也降低，即对舵机频带的要求也可随之降低，然而增稳回路新弹体的快速性和阻尼系数均下降。

2.4 三回路驾驶仪

三回路驾驶仪是在增稳回路的外层通过过载反馈构成的闭环控制系统，如图4 所示。其中，kA、ωI和kg为设计参数。

图4 三回路驾驶仪Fig.4 Three－loop autopilot

三回路驾驶仪的闭环传递函数具有如下形式:

式中:J3、J2、J1为闭环特征多项式系数;KC3为闭环增益。其表达式如下

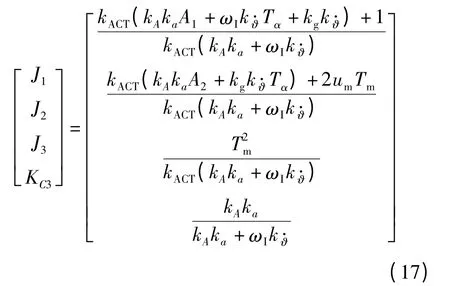
将(16)式的特征多项式分解为一阶和二阶环节的积，得到

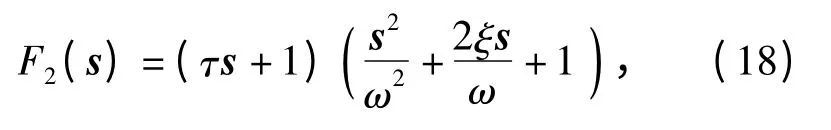
式中:τ 为一阶环节的时间常数;ω 和ξ 分别为二阶环节的角频率与阻尼系数，不失一般性，设ξ =0.5，解得

忽略由舵面升力带来的高频零点对闭环系统动态性能的影响，即A1≈0，A2≈0，同时设开环弹体参数Tm≪1，μm≪1，当ωITα≫kg≫2umTm/kϑ·Tα时，一阶环节为闭环主导模态，那么有

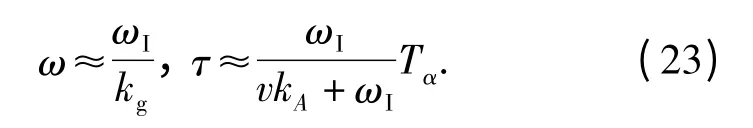
上述分析表明:1)一阶环节时间常数τ ＜Tα，时域响应比增稳回路快，且其快速性可通过设计参数调节;2)二阶环节的频率可由设计参数决定;3)当kg一定时，ωI的取值越大，二阶环节越快，一阶环节越慢。综上所述，三回路驾驶仪能够通过调节设计增益使一阶慢根为闭环主导极点，并“远离”开环弹体极点，且高频振荡极点的可控性较强，使控制系统具有较高的鲁棒性。

若要求三回路驾驶仪稳定，需满足不等式组

达到临界稳定时三回路驾驶仪和增稳回路设计增益的比分别为

分析表明:二者的阻尼回路设计增益kg基本一致;当aα＞－ωCRbα时，ωITL比ωISL略小，说明过载闭环后需要更大的反馈控制增益保证系统稳定性。

2.5 对静不稳定弹体的增稳能力对比

x*=aα/bα表征了静不稳定弹体的静稳定度，在临界稳定时，由不等式(7)式、(13)式、(24)式可分别得到阻尼回路新弹体、增稳回路新弹体和三回路驾驶仪的控制器参数对于x*的约束关系分别如(27)式～(29)式所示，且当x*的下限值越小，表明控制系统对静不稳定弹体的增稳能力越高。

1)阻尼回路新弹体

2)增稳回路新弹体

当ωCR＞－aω－bα时，有

3)三回路驾驶仪

当ωCR＞－ aω－bα且kA＞－ωI/v 时，有

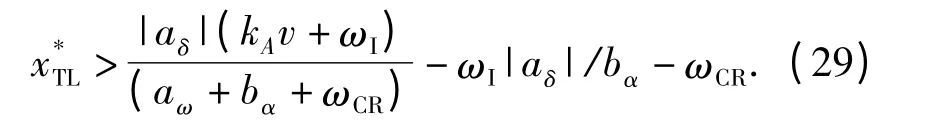
上述分析表明，当设计增益满足不等式(30)式时

3 种控制系统对被增稳弹体的x*下限值之比约为

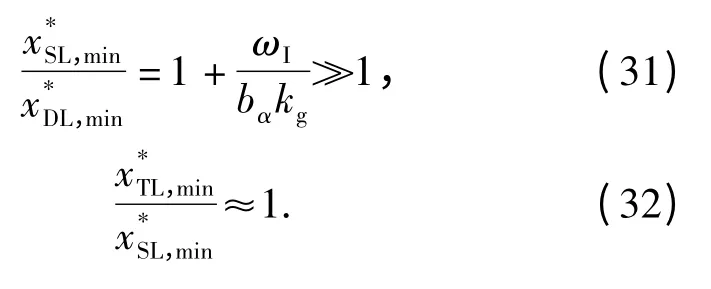
(31)式、(32)式表明，增稳回路对静不稳定弹体的增稳能力相比阻尼回路大幅提高，而三回路驾驶仪与增稳回路基本一致。综上所述，三回路驾驶仪的增稳回路能够有效提高控制系统的稳定性;过载反馈闭环之后，在提高系统响应速度的同时，对弹体的增稳能力依然较高。

3 三回路驾驶仪的无量纲分析

3.1 三回路驾驶仪的无量纲化

为便于分析设计参数对控制系统的影响，将三回路驾驶仪进行无量纲化。设闭环系统(16)式的低频主导极点和高频振荡极点分别为p1、p2和p3，为保证系统具有良好的稳定性，三回路驾驶仪的闭环极点均为LHP 极点，并存在如下关系:

上述分析表明，τ、ω 和ξ 是三回路驾驶仪的主要性能参数，并能够与闭环极点相互表示。在给定状态空间描述下，利用输出反馈的极点配置方法[9]，三回路驾驶仪的闭环极点能够任意接近期望极点，从而使驾驶仪的设计参数与闭环极点一一对应，并以此确定系统的开环性能。为便于分析，采用无量纲化方法，研究三回路驾驶仪的设计参数、闭环极点、开环和闭环系统性能参数之间的对应关系。

令λ=ωτ 为无量纲时间常数，表征了低频极点与高频极点的距离。定义无量纲算子忽略高频零点的影响，得到三回路驾驶仪闭环传函的无量纲表达式为

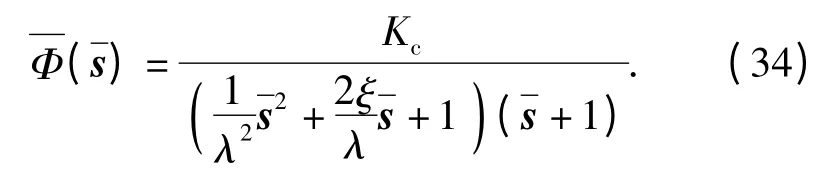
λ、ξ 和Kc决定了三回路驾驶仪无量纲系统的性能。在低频处较小而λ 较大，系统(34)式可近似为一阶惯性环节，传递函数为

3.2 无量纲系统的时域分析

为考察驾驶仪无量纲闭环系统的时域性能，令闭环增益Kc≈1，阻尼系数ξ=0.6[6]，获得三回路驾驶仪无量纲模型和一阶环节无量纲模型的单位阶跃响应上升时间随λ 的变化曲线如图5 所示。图6给出了当λ =7 时无量纲驾驶仪对单位阶跃过载指令的响应曲线。

图5 无量纲系统T63%随λ 的变化Fig.5 Non－dimensional λ

图6 无量纲驾驶仪的单位阶跃响应Fig.6 Response of the autopilot to a step command

仿真结果表明:1)驾驶仪和一阶环节的T63%近似，工程上可利用一阶环节近似估计三回路驾驶仪的时域性能;2)随λ 的增大而减小，当λ 足够大时趋近于1;3)当λ ＞5.5 时能够收敛至±20%的误差带以内;当λ ＞9 时基本不再随λ 变化;4)一阶环节为驾驶仪闭环主导环节。

3.3 无量纲系统的频域分析

通常弹体动力学的不确定性最大[7]，因此将三回路驾驶仪闭环模型在弹体环节处断开构成开环控制系统，其幅相裕度与穿越频率是驾驶仪的重要设计指标，在频域内考察λ 对相位裕度和穿越频率的影响。(36)式给出了驾驶仪的无量纲开环传递函数:

(36)式并不显含λ，且与弹体气动性能以及设计参数相关，但由前述对应关系可得到驾驶仪开环性能随设计指标的变化规律。令)的相位裕度为Pm，穿越频率为ωCRτ，在表2 给出的仿真条件下，Pm和ωCRτ 随λ 的变化曲线分别如图7 和图8 所示。研究结果表明:1)驾驶仪速度越快，随λ 增大，稳定裕度收敛越快;2)开环穿越频率随λ 近似线性变化，当λ 较大时，曲线的斜率ωCR/ω 约为常值;3)继续增大λ，稳定裕度将趋于常值，稳定性不再提高，而无量纲穿越频率将继续增大。

图7 开环相位裕度随λ 的变化Fig.7 Open loop phase margin versus λ

综上所述，本文提出了一种三回路驾驶仪的设计思路:通过增稳回路设计一个远离开环弹体频率且主要受系统设计参数决定的闭环一阶低频主导极点和一对阻尼合适的高频极点，在折衷了系统快速性的同时达到提高鲁棒性和稳定性的目的。控制系统付出的代价是:若增强低频极点的时域主导性需要增大高、低频极点间的频率差，而高频极点又直接影响驾驶仪的开环穿越频率以及舵机带宽，将导致响应较快的舵机系统搭配较慢的驾驶仪，使控制资源的利用率下降。

图8 无量纲穿越频率ωCRτ 随λ 的变化Fig.8 Non－dimensional crossover frequency ωCRτ versus λ

在驾驶仪设计中，首先根据总体需求确定控制系统快速性指标τ 和合适的阻尼系数ξ，其次选取合适的λ，同时检验开环穿越频率ωCR与舵机频带的匹配性和稳定裕度等指标，研究表明在保证舵机系统频带约为驾驶仪穿越频率的3 ～5 倍时，λ 可取6 ～9.该设计思路通过闭环系统设计并辅以开环指标检验，能够使驾驶仪具有合适的快速性、稳定性和鲁棒性。

4 结论

建立了纵向弹体控制模型，提出了三回路过载驾驶仪的两层内回路可独立构造新弹体的概念，并对比研究了开环弹体、阻尼回路新弹体、增稳回路新弹体和三回路驾驶仪的结构、快速性、鲁棒性以及对静不稳定弹体的增稳能力;推导了三回路驾驶仪的无量纲模型并进行了仿真分析;最后提出了一种三回路驾驶仪的设计思路。

研究结果表明:阻尼回路新弹体可抑制弹体摆动，但其增稳能力和鲁棒性较弱;增稳回路新弹体构造了一阶低频主导极点，具有良好的增稳能力和鲁棒性，但受弹体气动性能限制，其响应速度较慢;三回路驾驶仪的时频特性主要由设计参数决定，鲁棒性较强，其增稳回路提高了系统的稳定性，过载主反馈使驾驶仪具有较快的响应速度。

References)

[1]Mracek C P，Ridgely D B.Missile longitudinal autopilot:comparison of multiple three loop topologies[C]∥AIAA Guidance，Navigation，and Control Conference.San Francisco:AIAA，2005:2005 －6380.

[2]Mracek C P，Ridgely D B.Missile longitudinal autopilot:connections between optimal control and classical topologies[C]∥AIAA Guidance，Navigation，and Control Conference.San Francisco:AIAA，2005:2005 －6381.

[3]Wise K A.Robust stability analysisi of adaptive missile autopolit[C]∥AIAA Guidance，Navigation，and Control Conference.Keystone:AIAA，2008:1 －18.

[4]Kang S，Kim H J，Won D，et al.Robust roll－pitch－yaw integratedautopilot for a high angle－of－attack missile[C]∥AIAA Guidance，Navigation，and Control Conference.Keystone:AIAA，2008:2008 －7001.

[5]Nesline F W，Zarchan P.Robust instrumentation configuration for homing missile flight control[C]∥Guidance and Control Conference.Reston:AIAA，1980:209 －219.

[6]Zarchan P.Tactical and strategic missile guidance[M].5rd ed.Virginia:AIAA Inc，2007:483 －539.

[7]Garnell P，East D J.Guided weapon control systems[M].Oxford:Pergamon Press，1977.

[8]Lin D F，Fan J F，Qi Z K，et al.Analysis and improvement of missile three－loop autopilots[J].Journal of Systems Engineering and Electronics，2009，20(4):844 －851.

[9]Fan J F，Lin D F，Qi Z K，et al.Missile autopilot design using optimal control and frequency constraint[C]∥2nd International Syposium on Systems and Contron in Aerospace and Astronauties，ISSCAA，Shenzhen，China:IEEE，2008:1 －6.

[10]王辉，林德福，祁载康.导弹伪攻角反馈的三回路驾驶仪分析[J].系统工程与电子技术，2012，34(1):92 －98.WANG Hui，LIN De－fu，QI Zai－kang.Design and analysis of missile three－loop autopilot with pseudo－angle of attack feedback[J].Systems Engineering and Electronics，2012，34(1):92 －98.(in Chinese)

[11]Wang H，Lin D F，Wang J，et al.Design and analysis of missile two－loop autopilot with PI compensator under Multi－constraints[C]∥3rd International Conference on Advanced Computer Theory and Engineering (ICACTE).Chengdu IEEE，2010:V5－117－121.

[12]魏先利，夏群力，祁载康.姿态及过载自动驾驶仪比例导引对比研究[J].弹箭与制导学报，2003，23(4):5 －8，12.WEI Xian－li，XIA Qun－li，QI Zai－kang.Comparing study of proportion navigation guidance law of attitude and acceleration autopilots[J].Journal of Projectiles，Rockets，Missiles，and Guidance，2003，23(4):5 －8，12.(in Chinese)