不同过载自动驾驶仪的对比研究

姜易阳

(北京机电工程研究所，北京100074)

不同过载自动驾驶仪的对比研究

姜易阳

(北京机电工程研究所，北京100074)

针对三种不同结构的过载自动驾驶仪进行了对比研究，推导了驾驶仪控制回路的闭环传递函数，并对闭环稳态误差进行了分析。基于极点配置方法，设计了自动驾驶仪控制参数。在此基础上，研究了各驾驶仪控制回路对执行机构动力学延迟、非线性环节以及测量噪声的响应特性，并进行了对比分析，为飞行器过载自动驾驶仪的选型和设计提供了依据。

过载自动驾驶仪；三回路；伪攻角反馈

0 引言

自动驾驶仪是飞行器的重要组成部分，它的主要功能是在飞行包线范围内，维持飞行器的姿态运动和质心运动的稳定，并根据制导指令控制飞行器在一定的弹道上飞行。根据用途的不同，自动驾驶仪分为过载驾驶仪和角度控制驾驶仪两类[1]，目前使用较为普遍的是过载自动驾驶仪，结构主要有带PI校正的两回路过载控制结构、经典三回路过载控制结构[2]以及伪攻角反馈三回路过载控制结构等[3]，这三种过载自动驾驶仪具有相同的传感器需求，即均采用角速率陀螺测量弹体角速度，线加速度计测量弹体过载，但因结构的不同，使得其控制效果和鲁棒特性存在较大差异。

本文将理论推导和数学仿真结合，从稳态误差分析、参数极点配置、对非线性及噪声的适应性等方面，系统地对比了三种过载自动驾驶仪结构的异同，研究结论为飞行器过载自动驾驶仪的选型和设计提供了参考。

1 过载自动驾驶仪回路结构

本节以飞行器纵向过载控制为例，给出各自动驾驶仪的结构，并推导控制回路的闭环传递函数。回路中的弹体传递函数由线性化后的弹体动力学方程组推导得到[4]，如式(1)～式(3)：

(1)

(2)

(3)

1.1 带PI校正的两回路过载驾驶仪

带PI校正的两回路过载驾驶仪(以下简称两回路过载驾驶仪)在经典两回路过载驾驶仪的基础上发展而来，增加了过载跟踪误差的积分，以消除稳态误差，图1为采用该过载驾驶仪的控制回路结构框图。

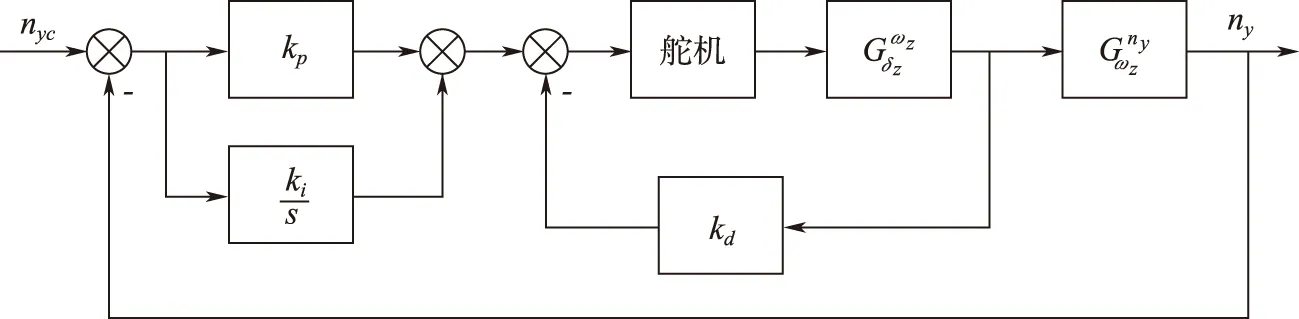
图1 两回路过载驾驶仪框图Fig.1 Structure of two-loop acceleration autopilot

其控制回路包含3个控制参数，忽略舵机环节，得到整个控制回路的闭环传递函数为

(4)

其中，各系数如下：

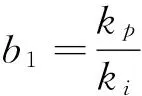
(5)

1.2 经典三回路过载驾驶仪

经典三回路过载驾驶仪在国内外飞行器上均得到了普遍应用，图2为采用该过载驾驶仪的控制回路结构框图，可见其包含3个回路，即阻尼回路、增稳回路和过载回路。共有4个控制参数，其中KDC用于补偿阶跃响应的稳态误差，使得回路闭环增益为1。

图2 经典三回路过载驾驶仪框图Fig.2 Structure of classical three-loop acceleration autopilot

忽略舵机环节，得到整个控制回路的闭环传递函数为

(6)

其中，各系数如下：

(7)

1.3 伪攻角反馈三回路过载驾驶仪

伪攻角反馈三回路过载驾驶仪(以下简称伪攻角反馈过载驾驶仪)也是一种三回路结构的过载驾驶仪，图3为其结构框图。对比图2、图3结构可知，经典三回路驾驶仪中的增稳回路为姿态角反馈，而伪攻角反馈驾驶仪将角速率陀螺的测量信号经过一个惯性环节后得到近似攻角，并将其作为增稳反馈。相比于经典三回路驾驶仪结构，其回路闭环增益为1，无需进行增益补偿。

图3 伪攻角反馈过载驾驶仪框图Fig.3 Structure of three-loop acceleration autopilot with pseudo angle of attack feedback

忽略舵机环节，得到整个控制回路的闭环传递函数为

(8)

其中，各系数如下：

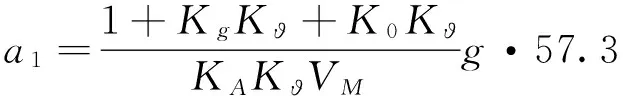
(9)

由以上分析可知，两回路过载驾驶仪传递函数存在零点，经典三回路驾驶仪需进行增益补偿，而伪攻角反馈过载驾驶仪需引入一项弹体动态特性参数，彼此各有特点。下面从稳态误差分析、参数极点配置、对非线性及噪声的适应性等方面进行详细对比研究。

2 回路闭环稳态误差分析

由式(4)可知，两回路过载驾驶仪的闭环稳态误差为0，且不受弹体动态特性摄动影响。对于经典三回路过载驾驶仪，因KDC与飞行速度相关，若速度存在测量误差，则闭环稳态误差不为0。考虑速度测量误差为ΔVM，则增益补偿为

(10)

根据驾驶仪结构可推得闭环传递函数如下

(11)

由终值定理可知，稳态误差为

(12)

可见经典三回路过载驾驶仪的稳态误差与速度测量误差及飞行速度相关，飞行速度越低，速度测量误差越高，则稳态误差越大。

忽略舵机环节，推导得到该回路结构的闭环传递函数如下

(13)

其中，各系数为：

(14)

可见，当控制回路使用的弹体动态特性参数存在误差时，回路闭环传递函数分母上升为四阶，并增加了一个零点，由终值定理可知，该条件下的回路闭环稳态误差仍为0，即伪攻角反馈过载驾驶仪的回路闭环稳态误差不受弹体动态特性摄动及速度测量误差的影响。

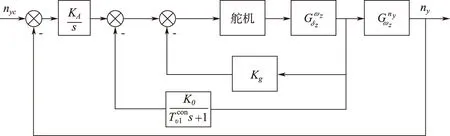
图4 伪攻角反馈过载驾驶仪框图Fig.4 Structure of three-loop acceleration autopilot with pseudo angle of attack feedback

3 驾驶仪控制参数极点配置

因各结构驾驶仪回路的闭环特征方程为三阶，可采用极点配置方法设置同时满足闭环回路稳定和时域特性要求的控制参数[5-6]。设极点配置所要求的3个极点由1对振荡根和1个负数实根组成，并设振荡根阻尼为μ，自振频率为ω，一阶滞后环节时间常数为τ，则系统期望的闭环特征方程为

(15)

完成极点配置应有回路闭环传递函数的分母各项系数与式(15)对应系数相等，得到3个方程，即可解得各控制回路的控制参数。将各过载驾驶仪控制回路的极点配置设为一致，得到阶跃响应曲线对比如图5所示。由曲线可知，因两回路控制闭环传递函数存在零点，其阶跃响应与期望回路响应相差较大，且存在超调；而对于经典三回路及伪攻角反馈三回路控制结构，将其极点配置固定后，回路阶跃响应与期望响应完全一致，这对回路设计与分析来说是个很大的优势。

由于采用极点配置，使得各驾驶仪控制回路的闭环传递函数极点相同，由自动控制理论可知，各控制回路的开环传递函数频率响应一致，图6为回路开环频率特性曲线，理论条件下回路的相角裕度和幅值裕度均较高。

图5 各过载驾驶仪回路阶跃响应对比曲线Fig.5 Step response of three acceleration autopilots

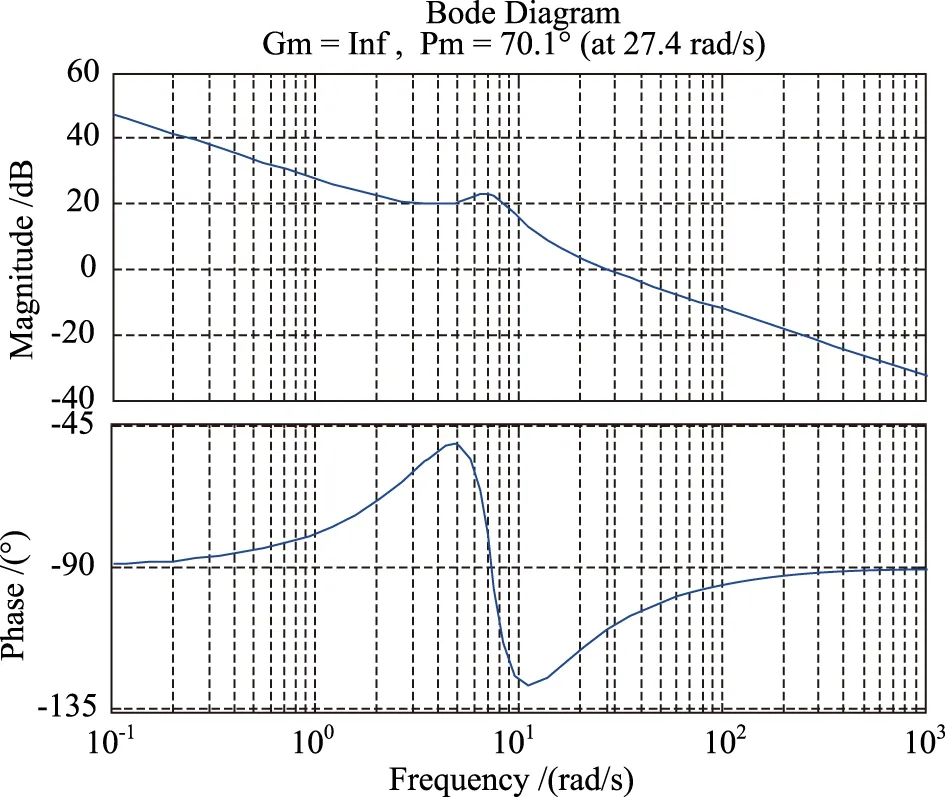
图6 开环频率特性曲线Fig.6 Phase-frequency characteristic of open loop

4 动力学和非线性环节的影响

第3节进行驾驶仪控制回路分析时忽略了舵机环节，然而舵机环节对回路的阶跃响应和回路裕度均有影响，甚至可能导致理论情况下的稳定回路发散。考虑如式(16)所示的舵机动力学环节

(16)

该舵机模型的带宽为13Hz。图7、图8分别为考虑舵机动力学环节后的回路阶跃响应曲线及开环频率特性曲线，可见回路的阶跃响应曲线变化较小，而频率特性受动力学环节的影响较大。在低频段，开环频率特性基本一致，随着频率的上升，舵机动力学环节带来的相位滞后和幅值衰减增大，使得回路的幅值裕度及相角裕度均有所下降。

图7 各过载驾驶仪回路阶跃响应对比曲线Fig.7 Step response of three acceleration autopilots

虽然各控制回路的裕度相同，但因回路结构的不同，阶跃响应存在区别，当延迟特性较大时该现象更为明显。图9、图10为在舵机环节输入前加入纯延时环节后各回路的阶跃响应曲线和舵偏角响应曲线。

可见，增大动力学环节的延迟后，两回路过载驾驶仪的阶跃响应超调已超出50%，且调节时间较长，而三回路过载驾驶仪对动力学延迟环节的适应性较两回路过载驾驶仪的强。另外，受设计、生产、加工等环节的影响，实际舵机不可避免地存在死区、间隙等非线性环节。其中，因舵机间隙环节会增大控制回路的相角滞后[7]，加大动力学延迟，其对飞行器控制系统的影响较大。图11、图12为考虑0.2°的舵机间隙条件下，不同驾驶仪结构回路的阶跃响应曲线及舵偏角响应曲线(局部进行了放大)。可以看到，两回路过载驾驶仪阶跃响应处于稳定的周期性振荡状态，而三回路过载驾驶仪的阶跃响应稳定无振荡，三回路结构的驾驶仪对舵机间隙的适应性较两回路结构的更强。

图8 开环频率特性曲线Fig.8 Phase-frequency characteristic of open loop(with or without actuator delay)

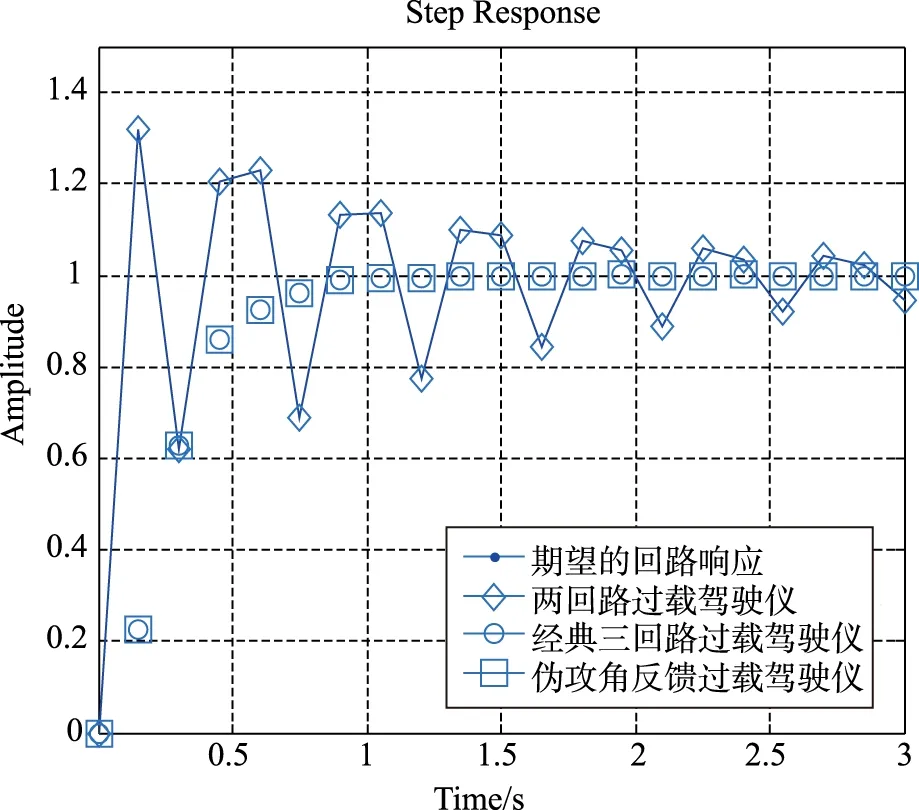
图9 各过载驾驶仪回路阶跃响应对比曲线Fig.9 Step response of three acceleration autopilots

图10 舵偏角响应曲线Fig.10 Actuator response of three acceleration autopilots

图11 各过载驾驶仪回路阶跃响应对比曲线Fig.11 Step response of three acceleration autopilots

图12 舵偏角响应曲线Fig.12 Actuator response of three acceleration autopilots

5 对测量噪声的抑制能力

对于采用纯比例导引或其改进形式作为导引规律的飞行器，控制回路输入的过载指令一般由导引头获取的视线角速度信号解算得到，其不可避免地存在测量噪声，对飞行器控制带来不利影响。图13、图14为在控制回路的输入端加入相同的零均值高斯随机白噪声后，回路的阶跃响应曲线及舵偏角响应曲线。

图13 各过载驾驶仪回路阶跃响应对比曲线Fig.13 Step response of three acceleration autopilots

可见三回路的驾驶仪结构对输入噪声的抑制要远强于两回路驾驶仪结构。进一步分析回路结构可知，两回路过载驾驶仪舵机输入信号中包含过载跟踪误差(即nyc-ny)的比例项，测量噪声直接输入舵机，而三回路结构的过载驾驶仪将过载跟踪误差经过了一个积分环节后，再作为舵机的输入，大幅降低了输入噪声的幅值和频率，有利于飞行器的稳定控制和执行机构的正常工作。

6 结论

本文针对三种典型结构的过载驾驶仪展开了对比研究，根据分析结果可知，三回路结构的过载驾驶仪在没有增加传感器需求的前提下，对动力学延迟、非线性环节及输入噪声的适应能力均强于两回路结构。经典三回路过载驾驶仪与伪攻角反馈过载驾驶仪的回路特性基本一致，但经典三回路过载驾驶仪的稳态误差与飞行器的速度测量误差相关，而伪攻角反馈过载驾驶仪的稳态误差不受气动摄动和测量误差的影响。在进行过载自动驾驶仪的选型时，若飞行器飞行速度较低且速度测量误差较大，伪攻角反馈过载驾驶仪更优。

根据本文的仿真分析，在引入舵机间隙环节后，两回路结构驾驶仪出现了极限环振荡，而三回路结构驾驶仪响应稳定无振荡，后续将采用非线性系统描述函数分析方法，对极限环的产生机理进行深入分析。

[1] 林德福，王辉，王江，范军芳.战术导弹自动驾驶仪设计与制导律分析[M].北京：北京理工大学出版社，2012.

[2] Paul Zarchan.Tactical and strategic missile guidance[C].Progress in Astronautics and Aeronautics，AIAA，2002.

[3] 王辉，林德福，祁载康.导弹伪攻角反馈三回路驾驶仪设计分析[J].系统工程与电子技术，2012，34(1)：129-135.

[4] 李新国，方群.有翼导弹飞行动力学[M].西安：西北工业大学出版社，2005.

[5] 朱敬举，祁载康，夏群力.三回路驾驶仪的极点配置方法设计[J].弹箭与制导学报，2007，27(4)：8-12.

[6] 刁兆师，单家元.基于预测校正的三回路驾驶仪极点配置设计[J].系统工程与电子技术，2012，34(8)：1668-1674.

[7] 程鹏.自动控制原理[M].北京：高等教育出版社，2007.

Comparative Study on Three Acceleration Autopilots

JIANG Yi-yang

(Beijing Electro-mechanical Engineering Institute，Beijing 100074，China)

Three different types of acceleration autopilot have been analyzed in detail.Based on the closed-loop transfer function derivation，the steady state errors of each control loop have been compared.The gains of the autopilot were derived through pole assignment method.Step responses of three autopilots with dynamic delay，non-linear element，and measurement noise have been evaluated.The comparative study provides the basis for acceleration autopilot design and selection.

Acceleration autopilot；Three-loop；Pseudo angle of attack feedback

2015-05-07；

2015-06-11。

姜易阳(1987-)，男，工程师，主要从事飞行器制导与控制技术方面的研究。

TJ765.2

A

2095-8110(2016)01-0040-07