一阶直流动态电路三种响应的仿真研究

纪明霞　王翠珍　王高翔

摘要：一阶直流动态电路是电路理论中的重要内容，其三种响应会随着电路时间常数的不同而表现出不同的特性。该文利用Multisum强大的仿真功能，对三种响应在不同时间常数情况下的输出信号进行仿真，从中观察分析三种响应的其变化规律以及时间常数的大小对过渡过程长短的影响，有助于对一阶动态电路过渡过程的理解。

关键词：一阶动态电路；三种响应；时间常数；变化规律；过渡过程

中图分类号：TP391.9 文献标识码：A 文章编号：1009-3044（2016）29-0219-02

1概述

一阶直流动态电路的响应，根据换路后是由外加激励还是动态元件的初始储能产生的，分为三种情况。一种是换路后，仅有外加激励作用下的零状态响应；一种是换路后仅有动态元件的初始储能产生的零输入响应；还有一种是换路后由外加激励和动态元件初始储能共同作用下的全响应n～。对于这三种响应的数学分析，可以用微分方程法或三要素法求解得到所有响应精确的数学表达式，但数学表达式对于三种响应的实质以及变化规律体现的并不明显。通过Multisum对三种响应的仿真，不仅有助于对数学理论知识的巩固，而且有助于对一阶动态电路过渡过程相关知识点（譬如时间常数对过渡过程长短的影响等）的理解。

2Muitisum主要功能及特点

Multisim是加拿大IIT公司推出的電子线路仿真软件EWB的升级版，它把电路图的创建、电路的测试分析和仿真结果等内容集成在一个电路窗口中。Multisim的元器件库提供了数千种类型的元器件，其中的虚拟元器件可根据需要任意修改元件参数。Multisim还提供了众多的虚拟仪器，如示波器、波形发生器等，其功能与实际仪表相同，可方便地进行电路的仿真测试分析。Muhisim的电路分析功能十分强大，能进行直流工作点分析、交流分析、傅里叶分析等多种分析。利用Muhisim强大的仿真功能，对动态电路过渡过程的分析是一条行之有效的思路。

3一阶直流动态电路的三种响应及其仿真

一阶动态电路根据所含动态元件（L或C）的不同，分为一阶RC动态电路和一阶RL动态电路，两者在分析方法上具有很强的对偶性，所以我们着重介绍RC一阶动态电路的三种响应及其仿真。

3.1零输入响应与零状态响应及其仿真

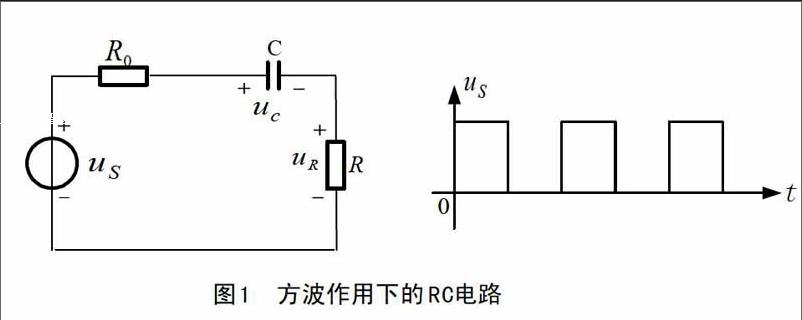
由于RC电路的时域响应，一般都是短暂的一次过渡过程。为了便于观察过渡过程中零输入响应与零状态响应的变化规律，采用周期变化的方波电压作为电路的激励电源，以便使过渡过程重复出现（如图1所示）。只要方波电压的半个周期T/2（也就是信号作用的时间）大于过渡过程的持续时间，则方波输出Us=0时，其所在电路部分相当于一条短路线，此时电路为零输入响应，Us#0时，就相当于电路的零状态响应。

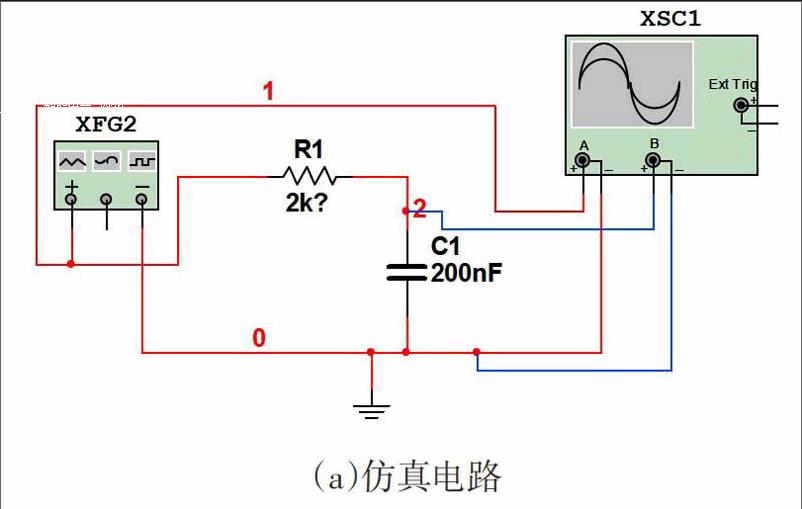
图2（a）为图1的仿真电路图，其中信号发生器XFG2设置为方波（占空比duty cycle为50%），频率100Hz，幅度（ampulitude）为5Vp。从仿真图中可以看出以下几个知识点：

3.1.1种响应的变化规律

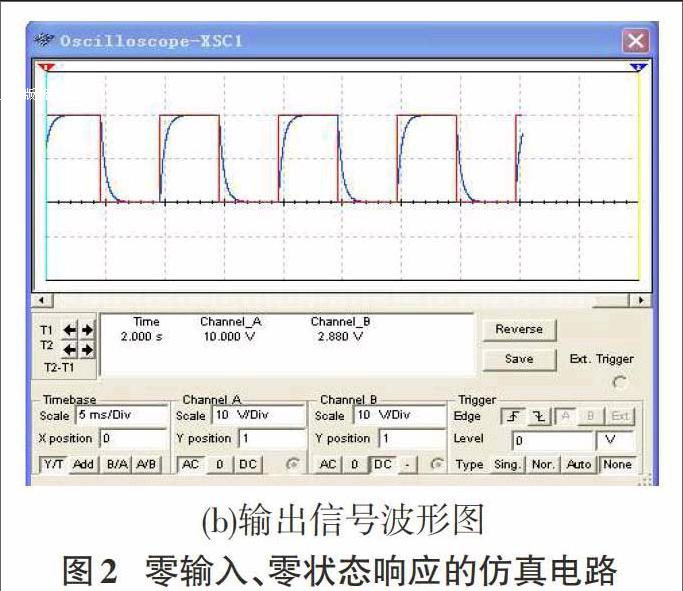
图2（b）为R=2K，C=200nf=0.2uF，即时间常数τ=RC=0.4ms的波形图。由于方波电压的半个周期时间为t=1/2f=0.005s=5ms>>τ=0.4ms，所以，从图中很明显看到零状态响应（Us≠0期间）和零输入响应（Us=0期间）的过渡过程皆早已结束，电路处于新的稳态，零状态响应电容两端的电压按照指数规律增长，最终充电完毕约为电源电压10V；零输入响应电容两端的电压按照指数规律衰减，最终趋向于0V。

3.1.2间常数τ与过渡过程长短的关系

当外加激励不变，改变电路中电容或电阻的参数，譬如将电容的值增大为C=2μF（τ=RC=4mS），则仿真的波形如图3（a）所示。从图中可以看出零状态响应，在方波下降沿到来时，电容两端电压远小于外加激励10V，过渡过程没有结束。同理零输入响应电源上升沿到来时，电容两端电压值远大于0，电容也没有放电完毕。这充分说明时间常数增大，过渡过程变长。

当继续增大时间常数，大约τ≈（3～5）T/2（C=7.5μF，τ=RC=15ms）得到如图3（b）所示波形，很明显，过渡过程远没有结束，两种响应波形近似为直线，体现了电容充放电很慢，过渡过程更长，输出几乎为三角波，近似为输入方波信号的积分，所以当RC电路的时间常数很大时，输出信号取自电容两端的电路工程上又称为积分电路。

若再继续增大R或C值，使T值增大到约为信号持续时间的10倍时，此时若从电阻两端输出信号，可以发现电阻两端电压波形几乎与输入信号重合，即u_R=u_S，也就是的电路工程上称为耦合电路。反之在时间常数很小的情况下（信号持续时间约为10倍的τ值），输入为方波，仍从电阻两端输出信号，可以发现输出信号波形形成尖脉冲，电容充放电非常快，输出近似为输入的微分，即工程上的微分电路。这两种电路读者可以自行仿真。需要注意的是输入信号和示波器要共地。

3.2全响应及其仿真

全响应的仿真电路如图4所示，若开关J2先接在V2（或V1）端，处于稳定后，电容两端具有一定的初始值3V（或6V），再将开关合到V1（或V2）处，此时电容两端输出信号是由电压V1（或V2）和电容的初始储能共同产生的，仿真波形如图5所示。其中AB段表示的是开关J2先接在V2且处于稳态，将游标1定位在AB端，从窗口中的坐标读出此时电容两端电压为3伏；B点时刻开关动作合到6V电源V1处，BC段波形表明换路后，电容两端电压从初始值3V被充电，其波形按照指数规律增长到新的稳态值，将游标2定位在图中所示的稳定处，从窗口中的坐标读出此时电容两端电压为6V，正好等于外加激励值，电容充电结束；C点时刻则表示开关由电源6V处动作合到3V电源处，此时电路中的响应也是有电容新的初始值（6V）和电源（3V）共同产生的全响应，CD段波形表明换路后电容两端电压从初始值6V放电，其波形按照指数规律衰减到新的稳态值3V，过渡过程结束，之后DE段重复AB段。由此波形分析得到全响应的变化规律：总是从初始值开始，按照指数规律过渡到稳态值（初始值>稳态值，按照指数规律衰减；初始值<稳态值，按照指数规律增长），过渡过程的长短和零输入、零状态响应一样取决于电路的时间常数，在此不再累述。

4结束语

一阶动态电路过渡过程的分析就是要分析三种响应中电压与电流的变化规律，以及影响变化规律的参数。通过本文中Mulfisum的仿真波形，可以形象直观地观察到三种响应的变化规律以及时间常数的大小对过渡过程长短的影响。不仅如此，对于外加非线性激励的一阶动态电路，采用数学微分方程求解的方法则变得更为繁琐，但若用Mtdtisum仿真，则跟本文中一样，简便、快捷、形象直观。