大挠度简支矩形薄板受热力磁耦合作用分岔与混沌

王 平，陈蜀梅，王知人2，

(1.燕山大学 建筑工程与力学学院，河北秦皇岛 066004;2.中国科学院 力学研究所非线性力学国家重点实验室，北京 100080;3.燕山大学 理学院，河北秦皇岛 066004)

弹性物体中耦合场理论的创立与发展，对处在高温、高压及强电磁场作用下结构元件强度和可靠性分析具有重要意义［1］。随着电磁结构在高新技术领域中的应用日益增多，针对工程中许多构件工作在温度变化环境中，对电磁耦合热弹性现象的研究有非常强的工程背景与理论价值［2-3］。热弹耦合振动以热弹耦合与振动理论为基础发展而来的新兴研究方向。Trajkorski等［4］分析了给定边界条件下圆板热弹耦合振动特性。戴宏亮等［5］研究了厚壁圆筒在热、磁耦合作用下的动态响应。树学锋等［6-7］建立圆板横向热弹耦合振动方程，并对常厚度及变厚度圆板非线性热弹性耦合振动进行分析。Yeh［8］研究大变形简支正交异性矩形薄板的热弹耦合振动。

混沌动力学的不断发展与完善极大丰富了非线性科学的研究领域，为许多古老研究课题注入新的活力，为力学学科发展提供新的动力。目前，各种形式构件热弹性耦合振动的混沌运动研究，也取得一些成果。韩强等［9］考虑几何非线性效应与温度效应影响，建立椭圆板周期激励作用下热弹耦合的非线性动力方程，利用Melnikov函数法给出系统发生混沌运动的临界条件。吴晓等［10］研究了矩形板非线性热振动分岔。Yeh等［11］对热弹耦合矩形板分岔与混沌进行研究。李映辉等［12］研究了变温环境下粘弹性梁的混沌运动。

综上所述，由目前研究成果看，对非铁磁类材料大挠度矩形薄板在热、力、磁耦合共同作用下热磁性耦合振动的混沌运动研究尚少。因此本文针对大挠度矩形薄板，考虑温度场影响，研究在横向稳恒磁场与机械载荷共同作用下的非线性热磁弹性耦合振动问题。结果表明，薄板在多场耦合作用下，具有丰富的非线性动力行为。通过改变机械载荷、电磁场及温度场参数，可控制系统的振动特性。

1 运动方程

将矩形薄板置于横向稳恒磁场B(0，0，Bz)中，同时受分布载荷P(0，0，q)作用.在笛卡儿直角坐标系oxyz中，oxy为薄板中面，z为法向坐标，不考虑极化、磁化影响，将洛仑兹力［2］ρfx，ρfy，ρfz作为质动力载荷加入板运动方程，得薄板热、力、磁耦合运动方程为:

式中:h为板厚;q为法向机械载荷分量;Nx，Nxy，Ny;Qx，Qy;Mx，Mxy，My为内力分量;θx，θy为角位移分量;ρ为质量密度;ρfx，ρfy，ρfz分别为对应x，y，z的洛仑兹力分量;mx，my为洛仑兹力矩。

洛仑兹力与洛仑兹力矩为［2］:

式中:u，v，w分别为中面内点x，y，z向位移;t为时间;σ为电导率;ex，ey为磁感应电场强度分量。

矩形板在热状态下的内力方程为［13］:

中面内力及挠度表示的相容方程为［14］:

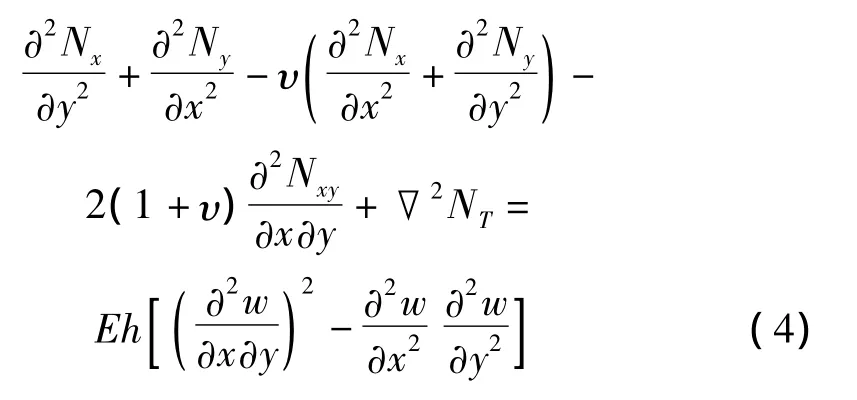
式中:NT为热力。热力、热矩的表达式为［14］:

式中:α0为热膨胀系数。

引入应力函数φ(x，y):

令机械载荷q=q0cos(ωt)，其中q0为机械力幅值，ω为激振频率。式(1)后三个式子中去掉惯性力项，由式(1)～式(4)及式(6)可得矩形板在热状态下非线性控制方程为:

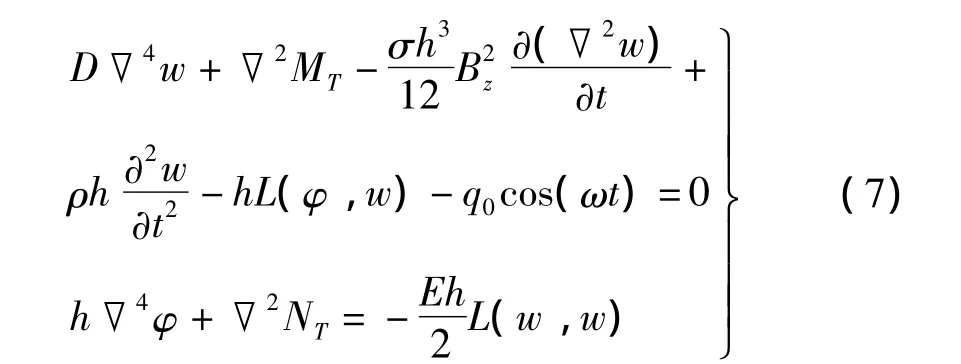
矩形薄板四边为不可移简支，a、b为板边长，边界条件为:

板端部表达式为:

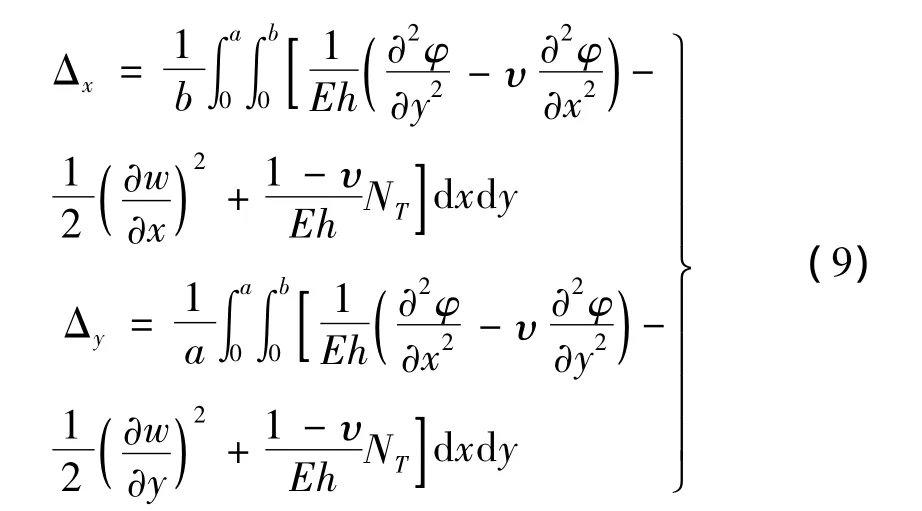
设温度函数为:

式中:T0为常数。由于工程实际中对最低阶振型感兴趣，故设:

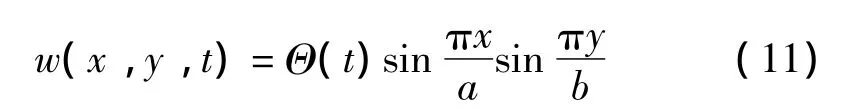
由式(5)、式(7)及式(11)得:

利用待定系数法［16］，设应力函数为:

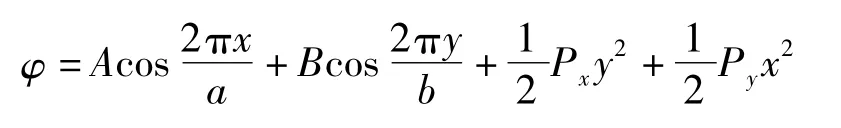
将其代入上式，两边比较系数，得:

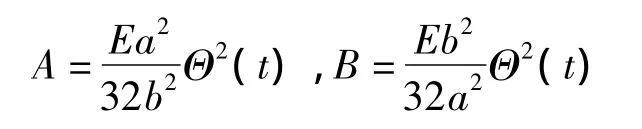
则应力函数为:

式中:Px，Py由式(9)求得(令:Δx=Δy=0)

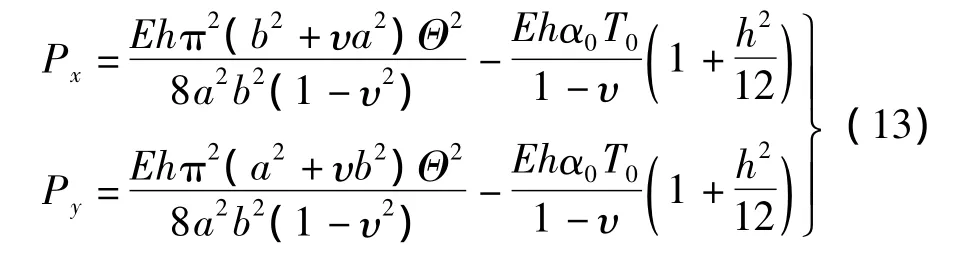
对式(7)中第一式利用Galerkin原理有:

将式(5)、(6)、(11)、(13)代入上式，计算得:

式中:

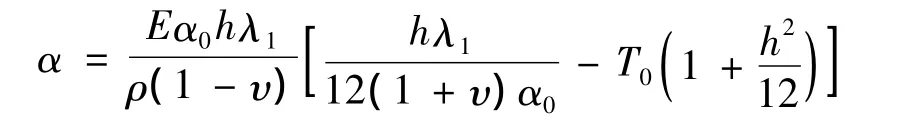
由β表达式看出β＞0，令η=|α|，则式(14)变为:

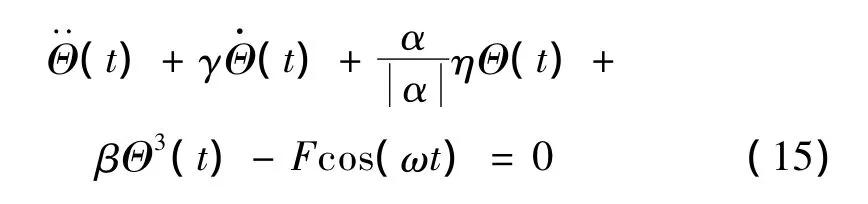
当ε=0时，式(17)为未扰动的Hamilton系统，即:

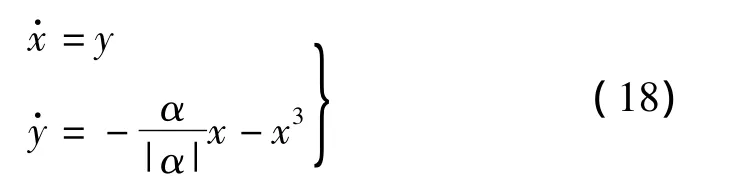
讨论α＜0情况，即式(16)为:

当α＜0时，未扰动的Hamilton系统有三个奇点，两个鞍点(±1，0)和一个中心点(0，0)。

2 数值解及算例分析

设薄板为铝质材料。板厚h=2×10-2m，密度ρ=2.67 ×103kg/m3，弹性模量E=71 GPa，泊松比ν=0.34，电导率σ=3.6 ×107(Ωm)-1，热膨胀系数α0=23×10-6(℃)-1。为便于计算，且α＜0，取a=3π m，b=2π m，ω0=1 rad/s。将其代入方程，用四阶R-K方法编程求解。计算中采用积分容忍误差为10-6。为模拟矩形薄板的混沌运动，采样周期为120，在积分所得时间响应中反复4 000次后开始取资料，以去掉足够的瞬态，保证系统动态响应已达到稳定状态。资料包括位移、加速度、时间等，用于产生分岔图、位移波形图、相平面轨迹图、及庞伽莱截面图。

2.1 机械载荷影响

当ω0=1 rad/s，Bz=1 T，T0=20℃时，通过改变机械载荷幅值q0大小，使f在0.01～10 N/m2之间变化，得系统随f变化时的分岔图(图1)。从图中看出，以机械载荷f为分岔参数，随着机械载荷幅值q0的不断增加，系统的混沌与周期区交替出现。在f=0.2 N/m2附近，系统由周期1运动经由阵发性进入瞬间混沌运动，转而又开始周期1运动，当f在1～1.6 N/m2之间系统有大面积混沌区，期间也存在一些零散的周期窗口，f=1.6 N/m2时系统离开混沌运动状态进入周期3运动，在f=1.8 N/m2附近转而又开始周期6运动，f在2～2.3 N/m2之间系统处于周期2运动状态，之后进入混沌区，在f=3.1 N/m2附近系统离开混沌进入周期1运动，后经由倍周期分岔，在f=4.8 N/m2附近进入混沌运动。后面空白处为周期窗口，之后再次进入混沌运动状态，如此反复。图2～图3给出在不同f值下系统位移波形图、相平面轨迹图及庞加莱截面图。当f=0.5 N/m2时，系统处于单周期运动状态;f=1.6 N/m2时，系统处于3周期运动状态;f=4.5 N/m2时，系统处于2周期运动状态;f=6.5 N/m2时;系统处于混沌运动状态。

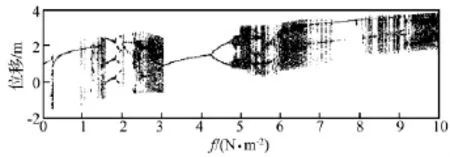
图1 ω0=1 rad/s，Bz=1 T，T0=20℃时系统随f变化时的分岔图Fig.1 Bifurcation diagram henf is variable(ω0=1 rad/s，Bz=1 T，T0=20℃时)

图2 f=0.5 N/m2时的位移波形图，相平面轨迹图及庞加莱截面图Fig.2 Wave diagram of displacement，Phase diagram and Poincare map(f=0.5 N/m2)

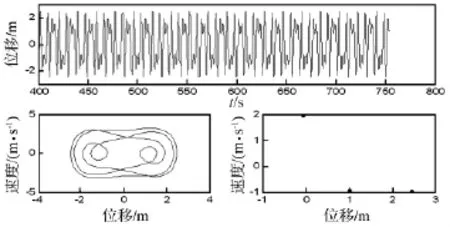
图3 f=1.6 N/m2时的位移波形图，相平面轨迹图及庞加莱截面图Fig.3 Wave diagram of displacement，Phase diagram and Poincare map(f=1.6 N/m2)

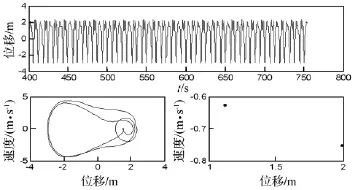
图4 f=4.5 N/m2时的位移波形图，相平面轨迹图及庞加莱截面图Fig.4 Wave diagram of displacement，Phase diagram and Poincare map(f=4.5 N/m2)

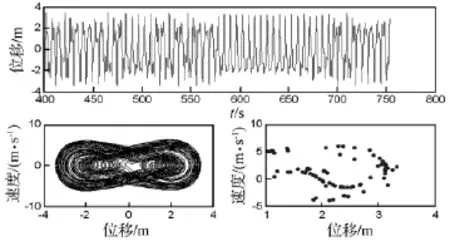
图5 f=6.5 N/m2时的位移波形图，相平面轨迹图及庞加莱截面图Fig.5 Wave diagram of displacement，Phase diagram and Poincare map(f=6.5 N/m2)

2.2 电磁场影响

当ω0=1 rad/s，T0=20℃，f=1.5 N/m2(q0=0.766 9 N/m2)时，通过改变磁感应强度大小，Bz取0.01～2T，得系统分岔图如图6所示。由图中看出，随着磁感应强度Bz的不断增加，系统运动状态有较明显变化。当Bz小于0.45T，系统一直处于混沌运动状态;在Bz=0.45T附近进入3周期运动状态;在Bz=0.78T附近离开3周期运动状态进入混沌运动状态;在Bz=0.78～1.28T范围内，系统基本处于混沌运动状态;在Bz=1.2T附近空白处有微小周期窗口;在Bz=1.28～2T范围内系统基本处于单周期运动状态;只是在Bz=1.45T左右有短暂的3周期运动。图7～图9为不同Bz值下系统位移波形图、相平面轨迹图及庞伽莱截面图。Bz=0.2T时，系统处于混沌运动状态;Bz=0.6T时，系统处于3周期运动状态;Bz=1.6T时，系统处于单周期运动状态。

图 6 ω0=1 rad/s，T0=20℃，f=1.5 N/m2时系统随Bz变化时的分岔图Fig.6 Bifurcation diagram whenBzis variable(ω0=1 rad/s，T0=20℃，f=1.5 N/m2)

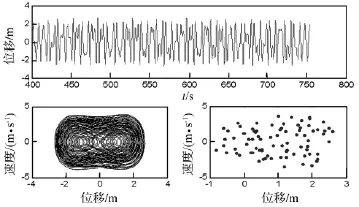
图7 Bz=0.2T时的位移波形图，相平面轨迹图及庞加莱截面图Fig.7 Wave diagram of displacement，Phase diagram and Poincare map(Bz=0.2T)

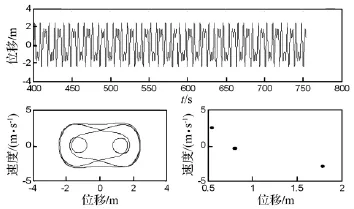
图8 Bz=0.6T时的位移波形图，相平面轨迹图及庞加莱截面图Fig.8 Wave diagram of displacement，Phase diagram and Poincare map(Bz=0.6T)

2.3 温度影响

图9 Bz=1.6T时的位移波形图，相平面轨迹图及庞加莱截面图Fig.9 Wave diagram of displacement，Phase diagram and Poincare map(Bz=1.6T)

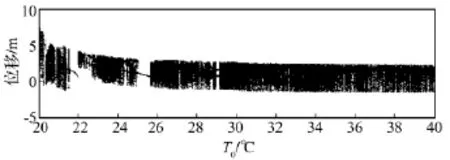
图10 ω0=1 rad/s，B=1T，q0=70 N/m2时系统随T0变化时的分岔图Fig.10 Bifurcation diagram whenT0is variable(ω0=1 rad/s，B=1T，q0=70 N/m2)

图11 T0=22℃时的位移波形图，相平面轨迹图及庞加莱截面图Fig.11 Wave diagram of displacement，Phase diagram and Poincare map(T0=22℃)

当ω0=1 rad/s，Bz=1T，q0=70 N/m2时，通过改变温度T0的大小(20～40℃)，得系统分岔图如图10所示。由图中看出，系统在T=22℃和T=25℃附近有短暂单周期区;在T=27℃和T=29℃附近及T=30～40℃范围内的空隙处存在微窄大周期区。图11～图14为在不同温度T0下系统位移波形图、相平面轨迹图及庞伽莱截面图。T=22℃时，系统处于单周期运动状态;T=27.8℃和T=29℃时，系统处于大周期运动状态;T=35℃时，系统处于混沌运动状态。

3 结论

(1)本文用Melnikov函数法，给出非线性动力系统Smale马蹄变换意义下出现混沌运动的判据.通过对系统进行数值模拟，在机械场、电磁场及温度场耦合作用下大挠度简支矩形薄板系统振动方程具有明显的非线性，运动特性较复杂，周期区与混沌区交替出现，混沌区中既有单周期窗口，也有倍周期窗口、大周期窗口，混沌与分岔现象较丰富。

图12 T0=27.8℃时的位移波形图，相平面轨迹图及庞加莱截面图Fig.12 Wave diagram of displacement，Phase diagram and Poincare map(T0=27.8℃)

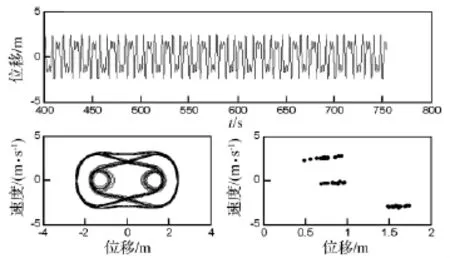
图13 T0=29℃时的位移波形图，相平面轨迹图及庞加莱截面图Fig.13 Wave diagram of displacement，Phase diagram and Poincare map(T0=29℃)

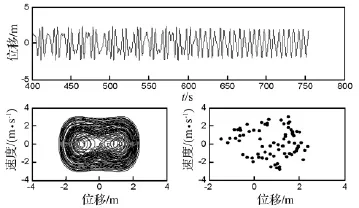
图14 T0=35℃时的位移波形图，相平面轨迹图及庞加莱截面图Fig.14 Wave diagram of displacement，Phase diagram and Poincare map(T0=35℃)

(2)单周期或k周期运动，对应相平面轨迹图为1条或k条连续的封闭曲线，在庞加莱截面图上显示1个或k个点，位移波形具有明显周期重复性;混沌运动，对应的相平面轨迹图轨线较紊乱，庞加莱截面图呈云片状、杂乱无章，位移波形呈类随机紊乱状态。

(3)通过变化机械载荷、电磁参数及温度可使系统进入混沌运动状态，或避免混沌运动，以实现对系统振动特性控制。本文研究结果可作为工程在温度环境下电磁结构安全性、可靠性设计参考。

［1］周又和，郑晓静.电磁固体结构力学［M］.北京:科学出版社，1999:1-8.

［2］白象忠.板壳磁弹性力学基础［M］.北京:科学出版社，2006.

［3］ Ghosh M K，Kanoria M.Generalized thermoelastic functionally graded spherically isotropic solid containing a spherical cavity underthermalshock［J］.Applied Mathematics and Mechanics，2008，29(10):1263-1278.

［4］ Trajkovski D，Cukic R.A coupled problem of thermoelastic vibrations of a circular plate with exact boundary conditions［J］.Mechanics Research Communications，1999，26(2):217-224.

［5］戴宏亮，戴庆华.厚壁圆筒在热磁耦合场作用下的动态响应［J］.动力学与控制学报，2003，1(1):78-83.

DAI Hong-liang，DAI Qing-hua.The dynamic responses of thick-walled cylinders under the coupling of temperature field and magnetic field［J］.Journal of Dynamics and Control，2003，1(1):78-83.

［6］树学峰，张晓晴，张晋香.周边固支圆板非线性热弹耦合振动分析［J］.应用数学和力学，2000，21(6):647-654.

SHU Xue-feng，ZHANG Xiao-qing，ZHANG Jin-xiang.Thermoelastic free vibration of clamped circular plate［J］.Mathematics and Mechanics，2000，21(6):647-654.

［7］李志刚，树学锋.一类变厚度圆板非线性热弹耦合的振动分析［J］.太原理工大学学报，2004，35(1):9-12.

LI Zhi-gang，SHU Xue-feng.Basic theory and method for analysing nonlinear thermoelastic vibration of round plate with variable thickness［J］.Journal of Taiyuan University of Technology，2004，35(1):9-12.

［8］ Yeh Y L.The effect of thermo-mechanical coupling for a simply supported orthotropic rectangular plate on nonlinear dynamics［J］.Thin-Walled Structures，2005，43(8):1277-1295.

［9］韩 强，张年梅，杨桂通.非线性热弹耦合椭圆板的混沌运动［J］.应用数学和力学，1999，20(9):896-901.

HAN Qiang，ZHANG Nian-mei，YANG Gui-tong.Chaotic motion of a nonlinear thermoelastic elliptic plate［J］.Mathematics and Mechanics，1999，20(9):896-901.

［10］吴 晓，马建勋.矩形板的非线性热振动分岔［J］.振动与冲击，1999，18(4):55-58，62.

WU Xiao，MA Jian-xun.The nonlinear thermal vibration bifurcation of rectangular plate［J］.Journal of Vibration and Shook，1999，18(4):55-58，62.

［11］ Yeh Y L，Chen C K，Lai H Y.Chaotic and bifurcation dynamics for a simply supported rectangular plate of themomechanical coupling in large deflection［J］.Chaos，Solitons Fractals，2002，13(7):1493-1506.

［12］李映辉，杜长城，高 庆.变温环境下粘弹性梁的混沌运动［J］.西安交通大学学报，2007，42(6):685-690.

LI Ying-hui，DU Chang-cheng，GAO Qing.Chaotic motion of a viscoelastic beam in time dependent temperature field［J］.Journal of Southwest Jiaotong University，2007，42(6):685-690.

［13］徐芝纶.弹性力学(上册，第三版)［M］.北京:高等教育出版社，1990:55-57，190-194.

［14］吴连元.板壳稳定性理论［M］.武汉:华中理工大学出版社，1996.

［15］高普云.非线性动力学:分叉、混沌与孤立子［M］.长沙:国防科技大学出版社，2005.