基于输入整形技术的太阳翼调姿残余振动抑制实验研究

那 帅，朱春艳，彭福军，唐国安，

(1.复旦大学 力学与工程科学系，上海 200433;2.上海市空间飞行器机构重点实验室，上海 201108;3.上海宇航系统工程研究所，上海 201108)

太阳翼为一端与航天器主体连接，另一端自由伸展的航天器能源采集组件，部分型号太阳翼的姿态调整由安装在根铰处的步进电机驱动。展开的太阳翼结构具有跨度大、厚度薄、刚度低、阻尼弱等特点，属柔性结构［1］，固有频率较低，而太空中几乎不存大气阻力，调姿激起的太阳翼残余振动很难自行衰减。该残余振动会影响航天器有效载荷的正常工作，降低其姿态稳定度与指向精度，缩短航天器及有效载荷的使用寿命。因此，采用被动或主动控制对调姿后太阳翼残余振动进行抑制非常必要。

传统的被动控制，如在太阳翼根部及表面加装阻尼材料或装置，结构简单、成本低。受结构质量、材料特性、空间环境等因素制约，减振效果不能满足对太阳翼振动控制的严格要求［2］。应用压电陶瓷、压电聚合物等压电材料为作动器主动控制技术发展迅速，控制效果显著［3-6］。然而，压电材料长时间暴露于太空强辐射及真空环境下的可靠性尚不清楚。同时，此类主动控制方案引进的作动器、相关控制配件及传感器元件会增加航天器的非有效载荷，对“能轻则轻”的航天器不利。对此，本文提出基于零位移输入整形技术(Zeroplacement Input Shaping Technique)对步进电机驱动太阳翼调姿残余振动抑制的前馈控制方案，以实现不增加航天器非有效载荷的同时大幅减小调姿激起的太阳翼残余振动［7-8］。

步进电机是将电脉冲信号转变为角位移的精确的开环控制元件。在非超载情况下，其转速与转角只取决于脉冲信号的频率和数量，而不受负载变化影响。本文从实验角度，设计、搭建了以步进电机驱动的太阳翼缩比梁模型，据其固有振动特性设计了相应的零位移输入整形器对调姿控制信号进行整形。通过将整形后控制信号转化成步进电机脉冲信号，借助VB开发的步进电机控制程序，实现了对实验模型调姿后残余振动的有效抑制，并对整形器的鲁棒性进行了实验分析。

1 实验设计

1.1 实验模型设计

图1为展开后的太阳翼结构示意图，安装于太阳翼根铰处的步进电机(图中未画出)输出调姿力矩，驱动太阳翼从初始姿态调整到目标姿态。整个调姿过程可用太阳翼根部所受步进电机施加的时变角位移载荷θ(t)描述。

图1 展开的太阳翼结构示意图Fig.1 Structure diagram of a deployed solar array

建立随太阳翼根铰转动的非惯性坐标系O-XYZ，太阳翼有限元模型在XOY平面内的横向弯曲振动运动方程为:

式中:M、C、K分别为模型的质量矩阵、阻尼矩阵、刚度矩阵;x={x1x2…xn}T为非惯性系内节点位移向量;ψ1为根铰加速度至节点加速度向量的变换矩阵，可借助将太阳翼模型绕OZ轴进行刚体模态分析获得。

仅关心太阳翼横向弯曲振动，忽略单块翼板间及太阳翼与航天器主体间的连接影响，认为太阳翼根铰在调姿过程中仅受调姿步进电机施加的角位移载荷，并忽略航天器轨道运行的刚体运动而将太阳翼随航天器刚体运动固化时，可将太阳翼简化为有集中质量的一维梁模型，梁根部与步进电机转轴固接，承受步进电机施加的时变角位移载荷θ(t)。

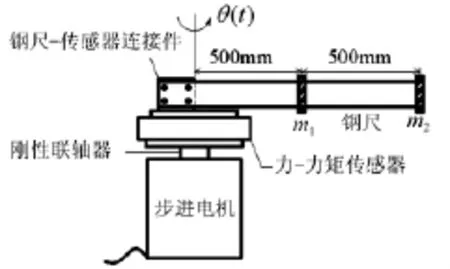
图2 实验模型简图Fig.2 Schematic diagram of the experimental model

图2为具有两个不同集中质量的太阳翼一维缩比梁模型，由长1 000 mm，宽35 mm，厚1.48 mm，密度7.564 g/cm3的不锈钢直尺代替，集中质量m1，m2分别用90 g，290 g金属块代替。为模拟太空无重力状态，实验模型水平放置，令横向弯曲振动平面与重力方向垂直，以保证振动方向无重力分量。实验以能反映梁模型振动强弱的根部竖直方向约束力矩为考察残余振动指标。具体做法是，将实验模型一端与某型号高强度刚性力-力矩传感器固接，并将该传感器通过刚性联轴器与步进电机转轴同轴连接。步进电机接收脉冲指令带动传感器转动，传感器对梁模型根部产生时变角位移激励的同时可采集梁根部的反作用力矩值。图3为实验装置图。

图3 实验装置实物图Fig.3 Photograph of the experimental facilities

1.2 整形器设计原理

如图4所示，输入整形是将初始指令与脉冲序列卷积生成的整形指令作为控制信号，以消除柔性系统残余振动非期望模态成分的前馈控制方法［9］。

图4 输入整形原理框图Fig.4 Schematic block diagram of input shaping technology

零位移输入整形法基于离散z平面的极-零点抵消，在非期望模态极点附近布置零点抵消目标极点［7］，从而抑制系统目标模态振动。

将式(1)动力学系统离散域内的传递函数表示为因式乘积形式:

式中:A为与系统固有频率及阻尼比有关的传递函数增益;l，n分别为系统共轭零、极点个数;zi，为系统第i对共轭零点;pj为系统第j对共轭极点，可引起系统第j阶弹性振动，形式为:

式中:ζj为系统第j阶模态阻尼比;ωnj，ωdj分别为系统第j阶固有频率及振动频率;T为离散采样周期。零位移输入整形思想即通过消除式(2)右端分母非期望极点消除系统对应模态的弹性振动。

将系统加入输入整形器的传递函数表示为整形传递函数H(z)与系统原传递函数G(z)的乘积形式:

为消除系统前m阶模态振动，H(z)应能抵消G(z)的前m对共轭极点。综合系统因果性及稳定性，将H(z)表示为:

式中:C为归一化调节参数，a1，…，a2m为关于自变量T的函数。为防止驱动器过载，T应在满足a1(T)，…，a8(T)均大于零的范围内取值。同时，为减小整形引起的系统响应迟缓，T的取值应尽可能小。为得到整形的调姿输入信号，利用映射关系z=exp(sT)及拉普拉斯逆变换，将式(5)变换到时域后与初始输入θ(t)卷积，得整形后的输入信号为:

1.3 整形器设计与残余振动抑制仿真

据式(5)，设计整形器时需确定系统的前m阶复特征值。利用MSC.Nastran，取实测的0.01全局结构阻尼因子对实验模型进行复特征值计算。为使计算值更接近真实值，需先对钢尺的弹性模量进行实测。即用图3的实验平台测量无集中质量的悬臂钢尺弯曲振动一阶固有频率，并代入悬臂梁基频公式:

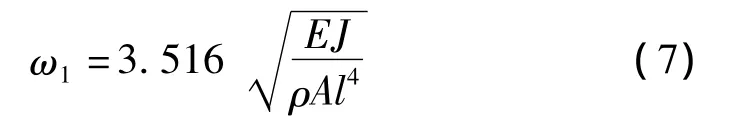
式中:J为钢尺截面对中性轴惯性矩，A为钢尺横截面积，ρ为密度，由计算得钢尺弹性模量为E=195 GPa。

考虑低阶模态更易引起太阳翼大幅振动，故在设计整形器时仅关心实验模型前四阶弯曲模态。将表1中前四阶复特征值代入式(3)，求出前四对共轭极点代入式(5)，得a1(T)，…，a8(T)，采样周取T=0.256 s，a1，…，a8函数值随之确定，见图5。

表1 系统前四阶模态复特征值Tab.1 Complex eigenvalues of the first four orders of the system

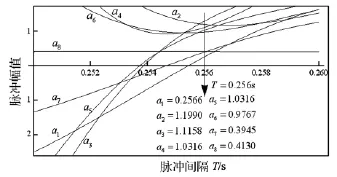
图5 整形器脉冲幅值Fig.5 Impulse amplitudes for the shaper

以表2太阳翼调姿工况5为例，整形后输入信号见图6。在此调姿信号激励下，实验模型根部竖直方向约束力矩的仿真结果见图7，整形后根部约束力矩的残余振动得到明显抑制。仿真结果表明，仅对实验模型前四阶模态施加前馈整形控制，便可大幅降低系统残余振动。

图6 工况5输入信号Fig.6 Input of operating mode 5

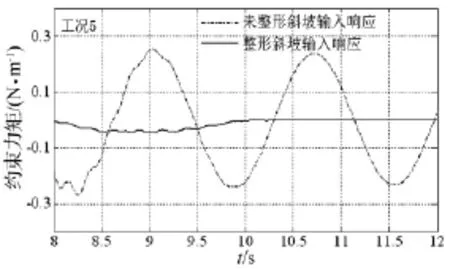
图7 工况5残余振动仿真Fig.7 Simulation of residual vibration of operating mode 5

表2 太阳翼调姿工况(单位:t/s，x(t)/rad)Tab.2 Operating modes for attitude control of the solar array(unit:t/s，x(t)/rad)

1.4 步进电机控制方案

图8为整个实验步进电机控制过程示意图。为实现对步进电机平稳精确控制，用高分辨率步进电机细分驱动器，将步进电机的实际步距角从0.02 rad缩小至0.000 5 rad。驱动器将PC接收的脉冲信号放大，并以脉冲频率交替为步进电机各相线圈通电，从而驱动步进电机以正比于脉冲频率的速度运转。图中虚线区域为整形器的设计过程，对确定的设计参数，此过程只需执行一次。

由于表2中太阳翼调姿工况是以角位移—时间关系描述的连续函数，无法直接用于控制步进电机，须对其进行近似处理。① 按式(8)将角位移—时间信号转换成步进电机脉冲—时间信号:

图8 控制过程示意图Fig.8 Control strategy of the system

式中:R()为四舍五入取整函数，θ(t)为转角弧度，K=12 800为步进电机细分驱动器参数(转一圈所需脉冲个数)。② 将所得脉冲—时间关系曲线沿时间轴分割成若干线性子区间。由于步进电机输出的转速正比于控制器单位时间输出的脉冲个数(脉冲频率)，故子区间线段斜率表示当前区间内的脉冲频率(输出转速)。子区间划分越密，控制步进电机脉冲信号越逼近理想控制信号，工况5离散脉冲—时间信号见图9，不难看出，随着离散时间间隔从1.5 s缩小到0.5 s，控制信号更逼近理想控制信号。为更好模拟理想整形后调姿信号，对所有工况整形输入信号均用0.05 s离散时间间隔，并以每段区间初末时刻脉冲数及区间线段斜率作为控制参数，调用VB定时器功能精确控制步进电机执行调姿指令。

图9 工况5离散脉冲—时间信号Fig.9 Discrete step-time signal of operating mode 5

2 实验结果及讨论

以20 Hz采样频率对分辨率0.01 N·m的传感器输出信号进行实时采集。图10为6种工况下实验模型在0～30 s区间内，受整形前后调姿输入信号引起的根部约束力矩变化情况。结合表2不难看出，由于工况1～5调姿速度较快、原始调姿信号引起的残余振动初始幅值较大，均达到0.5 N·m左右。但整形后残余振动初始幅值有效控制在0.1 N·m以内，平均约为整形前的17%。工况6调姿速度较慢，原始调姿信号引起的残余振动初始幅值约为0.2 N·m，通过输入整形，残余振动幅值有效控制在0.03 N·m左右，约为整形前的15%，整形效果显著。对比工况6与工况1～5，可看出整形效果的好坏与调姿动作的快慢无关，实际上，由式(4)知，整形器原理为消除目标阶模态振动，效果与原始输入信号形式无关。

同样，在每种工况调姿过程中，整形后信号引起的实验模型根部约束力矩幅值较未整形时成倍减小，即整形后的调姿信号对步进电机额定力矩要求下降。由此，可通过选择体积与功率更小的调姿作动器对太阳翼调姿定向，以达到节约机载能源、减轻航天器非有效载荷的目的。

3 残余振动抑制的鲁棒性分析

由式(3)、式(5)知，确定系统零位移输入整形器设计参数只依赖于非期望模态的复特征值，然而实验及数值模态分析均会产生模态辨识误差，影响整形效果。为考察整形器鲁棒性，设表1实验模型特征值为真实值，并分别上下调整10%、20%、30%，在其它条件不变情况下重新设计整形器，再对工况5进行调姿振动响应实验测量，所得实验模型根部约束力矩变化见图11，从图中不难看出，当系统模态识别误差为正时，整形器对实验模型残余振动的抑制效果与无识别误差时处于同一水平，甚至在存+20%误差时的整形效果更优，可能由此时的复特征值更接近模型实际特征值所致。存在-10%识别误差时的整形效果仍较理想。在存在-20%和-30%模态误差时，整形效果在9.5～10.5 s区间内较无误差时稍差，可能由此时的复特征值远离真实值所致，此时残余振动幅值仍与无误差时残余振动最大幅值处于同一水平，故不会对整形效果产生影响。可见，在存有一定系统参数误差情况下，整形输入仍能有效抑制实验模型残余振动。

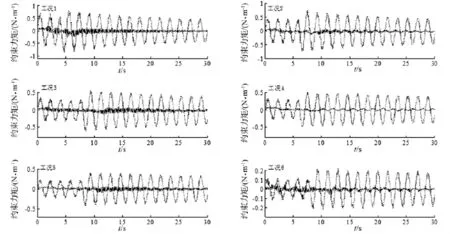
图10 整形前(虚线)后(实线)约束力矩比较Fig.10 Comparing of the constrain moment of unshaped input(dashed line)and shaped input(solid line)

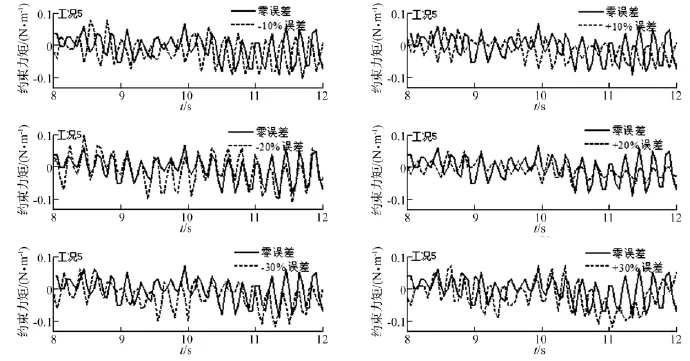
图11 存在模态辨识误差时的残余振动(工况5)Fig.11 Residual vibration when eigenvalues have errors(Operating mode 5)

4 结论

针对航天器太阳翼大角度快速调姿引起的残余振动，提出用零位移输入整形的前馈控制理论进行抑制。建立的以步进电机驱动太阳翼缩比梁模型，以整形后调姿信号控制步进电机对该模型进行6种工况的调姿实验。实验结果表明，将输入整形器应用于步进电机作动器的输入信号可将调姿激起的残余振动控制在整形前的20%以内，振动抑制效果显著。当系统存在±30%范围内的模态辨识误差时，整形器对残余振动抑制效果几乎不受影响，表明整形器具有较强鲁棒性。该控制方案整形器设计简单，用于航天器调姿驱动器，无需对现有航天器进行硬件改装或增加非有效载荷，可行性较高。该方法也有望应用于航天器在轨机动等导致太阳翼振动的抑制问题。

［1］李东旭.挠性航天器结构动力学［M］.北京:科学出版社，2010.

［2］ Maly J R，Pendleton S C，Salmanoff J，et al.Hubble space telescope solararraydamper［C］. Proc. SPIE， Smart Structures and Materials:Passive Damping and Isolation in Newport Beach，CA，1999:186-197.

［3］刘 强，何文杰，唐国安.采用电机驱动的太阳翼振动控制理论与仿真［J］.振动与冲击，2009，28(12):119-122.

LIU Qiang， HE Wen-jie， TANG Guo-an. Theoryand simulation of the solar array panel’s vibration control driven by electric motor［J］.Journal of Vibration and Shock，2009，28(12):119-122.

［4］ Meyery J L，Harringtony W B，Agrawal B N，et al.Vibration suppression of a spacecraft flexible appendage using smart material［J］.Smart Materials and Structures，1998，7(1):95-104.

［5］ Song G B，Agrawal B N.Vibration suppression of flexible spacecraft during attitude control［J］.Acta Astronautica，2001，49(2):73-83.

［6］ Hu Q L，Ma G F.Spacecraft vibration suppression using variable structure output feedback control and smart materials［J］.Journal of Vibration and Acoustics，2006，128(2):221-230.

［7］ Tuttle T D，Seering W P.A zero-placement technique for designing shaped inputs to suppress multiple-mode vibration［J］. ProceedingsoftheAmerican ControlConference，Baltimore，Maryland，1994，3:2533-2537.

［8］朱春艳，邵济明，那 帅，等.太阳电池翼调姿后残余振动抑制的整形器设计［J］.振动与冲击，2012，31(8):176-180.

ZHU Chun-yan，SHAO Ji-ming，NA Shuai，et al.Design and simulation of input shaper for residual vibration suppression after attitude adjustment of a solar array［J］.Journal of Vibration and Shock，2012，31(8):176-180.

［9］ Singer N C，Seering W P.Preshaping command inputs to reduce system vibration［J］.ASME Journal of Dynamic Systems，Measurement，and Control，1990，112(1):76-82.