基于改进峰值搜索法的旋转机械瞬时频率估计

胡爱军，朱 瑜

(华北电力大学 机械工程系，河北 保定 071000)

旋转机械在工业生产中应用广泛，不可或缺。为确保旋转机械的安全稳定运行，对旋转机械进行状态监测与故障诊断尤为必要。目前，状态监测的主要手段之一为振动监测。旋转机械升、降速过程的振动信号为典型非平稳信号，即旋转机械在稳定运行状态下，其转速是波动的，振动信号也具有非平稳性，不适合用常规的频谱法分析［1］。阶比分析为一种新的非平稳信号处理方法，通过等角度采样将时间域非平稳信号转化为角域平稳信号，对该信号进行分析可提取振动信号的非平稳特征［2］。传统的阶比分析方法分基于硬件的阶比跟踪与计算阶比跟踪。前者通过硬件实现转子的等角度采样，获得角域平稳信号;(而后者则对原始振动信号与转速脉冲信号同时进行等时间间隔采样，利用转速脉冲信号进行转速估计，由此获得等角度采样的发生时刻，并在此时对原始振动信号进行插值，实现等角度采样［3-4］。基于硬件的阶比跟踪对硬件要求较高，而计算阶比跟踪也需用健相装置测量转速，两种方法均较繁琐。为降低阶比跟踪对硬件的要求，文献［1］提出基于瞬时频率估计的阶比跟踪新方法，通过对原始信号时频分布进行峰值搜索获得一阶转速对应的瞬时频率，并取得一定效果。利用峰值搜索法从信号时频分布中获得转子的瞬时频率会受到信号中干扰频率成分影响，降低瞬时频率估计精度，影响阶比分析结果［5］。为降低干扰信号对提取瞬时频率影响，文献［6］提出STFT Viterbi拟合法进行瞬时频率估计，将原始信号进行STFT变换获得时频分布，在时频分布图中先确定瞬时频率起始点，利用Viterbi方法搜索下一个频率点，并取得一定效果。该方法需将频率范围分成多段，计算每个频率段内峰值对应的频率点，为确保某时刻瞬时频率点也在其中，必然会增大频率等分段数的选择难度。

为此，本文提出改进的峰值搜索法，通过小波分析获得原始信号的小波时频分布图。对时频分布图进行峰值搜索时，将瞬时频率中相邻两点一阶导数差值作为搜索峰值是否合理的判别条件，避免传统峰值搜索法在干扰信号作用下提取虚假峰值，提高瞬时频率的估计精度。

1 小波分析［7-9］

小波分析为多尺度时频分析方法。信号的时频特征(时间、频率、幅值等)可通过小波分解结果的时频参数获得。若ψ(t)为小波母函数，则需满足条件:

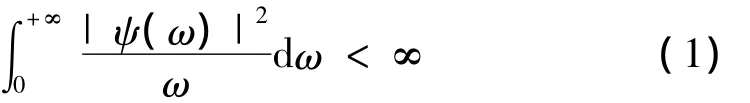
式中:ψ(ω)为ψ(t)的傅里叶变换。

通过对小波母函数平移及伸缩可得小波基函数:

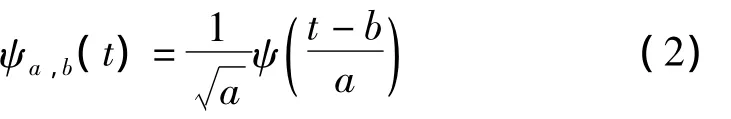
式中:a为尺度因子，b为平移因子。

若原始信号为s(t)，则其连续小波时频变换为:

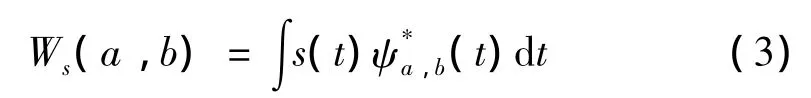
式中:(t)为ψa，b(t)的复共轭。

由尺度因子a及平移因子b的变化，可得小波系数Ws(a，b)，用灰度图表示可得小波时频分布灰度图。

2 改进的峰值搜索法

基于瞬时频率估计的阶比分析中，需利用原始信号估计参考轴转速。文献［1］利用峰值搜索法获得一阶转速，并计算原始信号的时频分布图，对时频分布图一阶转速附近进行峰值搜索，将峰值时刻对应的频率视为该时刻转子的瞬时频率，具体算法为:

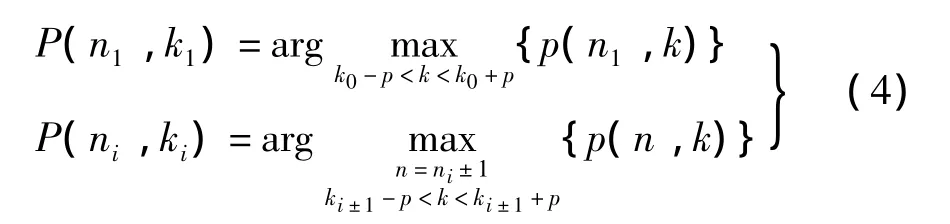
式中:arg max表示取最大值参数(此为k);p为设定的搜索范围;(ni，ki)为峰值坐标，即ni时刻对应的瞬时频率为ki。

当旋转机械振动信号中含幅值较大的干扰信号且该信号频率与一阶转速频率较接近时，利用式(4)搜索到的峰值将成为干扰信号峰值，其对应频率不再是一阶转速对应的频率，搜索到的一阶转速不再可靠。

旋转机械升速或降速过程中，在短时间段内参考轴作匀角加速运动［3，10］。据此知，旋转机械转速在任一短时间段内变化是平缓的，对应的时间—频率(转速)曲线一阶可导。在等时间间隔采样时，相邻两采样点的时间间隔较小，两个采样点对应的一阶导数近似相等。因此，本文提出改进的峰值搜索法，将相邻两点一阶导数差值作为搜索峰值是否合理的判别条件，避免传统峰值搜索法在干扰信号作用下提取虚假峰值。具体步骤为:

(1)选取信号时频分布图中一阶转速突出、与其它频率成分相距较远的区域据式(4)进行峰值搜索，确定相邻两峰值坐标(n0，k0)、(n1，k1)。

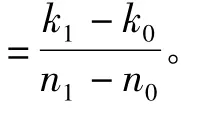
(3)设定n-1与n2时刻搜索范围分别为(k0-p，k0+p)与(k1-p，k1+p)。为确保瞬时频率点在搜索范围内，p取值应适当大。计算n-1时刻对应搜索范围内所有幅值，按幅值由大到小顺序，将该时刻幅值对应频率依次存入数组A;同样，计算n2时刻对应搜索范围内所有幅值，按幅值由大到小顺序，将该时刻幅值对应频率依次存入数组B。其中，A，B中第一个元素为最大幅值对应的频率。

(5)设定阈值s，分别比较ε-1，ε2与s的大小。若ε-1，ε2均小于s，认为此时A(1)与B(1)即为一阶转速在n-1和n2时刻对应频率;若ε-1大于s，则放弃A(1)，以A的下一点取代A(1)重复步骤(4)、(5);当ε-1小于s时，A(i)即为n-1时刻对应频率。同理，当ε2大于s时，可得n2时刻对应频率B(j)。

(6)用(n-1，k-1)、(n2，k2)取代点(n0，k0)、(n1，k1)重复步骤(2)～(5)可得(n-2，k-2)、(n3，k3)。依此重复可得各时刻一阶转速对应频率。

改进的峰值搜索法中，阈值s的选取影响瞬时频率提取效果。为讨论阈值s的选取，设(n0，k0)、(n1，k1)及(n2，k2)为时频图中瞬时频率相邻的3个点，有:

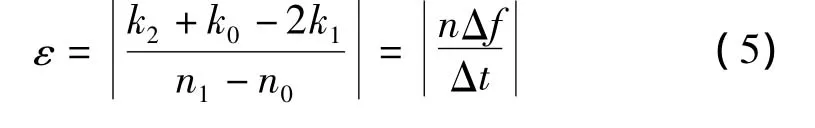
式中:Δt=n2-n1=n1-n0，Δf为时频分布图中相邻两频率点间隔，n=0，1，2…。

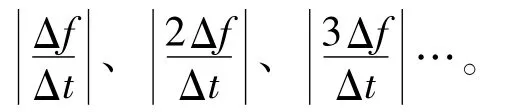
3 仿真信号分析

为证明改进峰值搜索法优势，分别利用传统峰值搜索法与改进峰值搜索法对仿真信号进行分析。采样频率fs=1 280 Hz，采样时间3.2 s，仿真信号为:

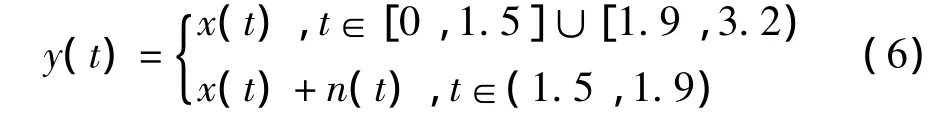
式中:x(t)=2sin(40πt2)，n(t)=8sin(100πt)。n(t)为在1.5～2 s间的干扰信号。对仿真信号进行小波时频分析，如图1所示。

图1中出现一条线性增大的瞬时频率曲线，与x(t)理论瞬时频率f=40t一致。同时，在1.5～2 s也可看到50 Hz的干扰信号n(t)，且频率与x(t)频率接近。

分别用传统峰值搜索法与改进的峰值搜索法计算仿真信号中x(t)瞬时频率。传统方法搜索范围与改进方法搜索范围均包含了干扰信号。前者计算的瞬时频率见图2，后者计算的瞬时频率见图3。

采用一次多项式分别对图2、图3中曲线进行最小二乘拟合。传统方法提取瞬时频率ft=38.86t-2.045，改进方法提取瞬时频率fi=39.4-0.203。理论瞬时频率、传统方法提取瞬时频率及改进方法提取瞬时频率如图4所示。

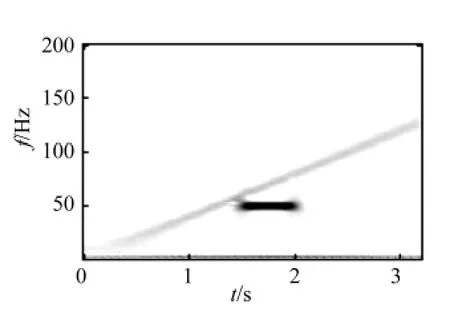
图1 仿真信号小波时频分布图Fig.1 Wavelet time-frequency diagram of simulation signal

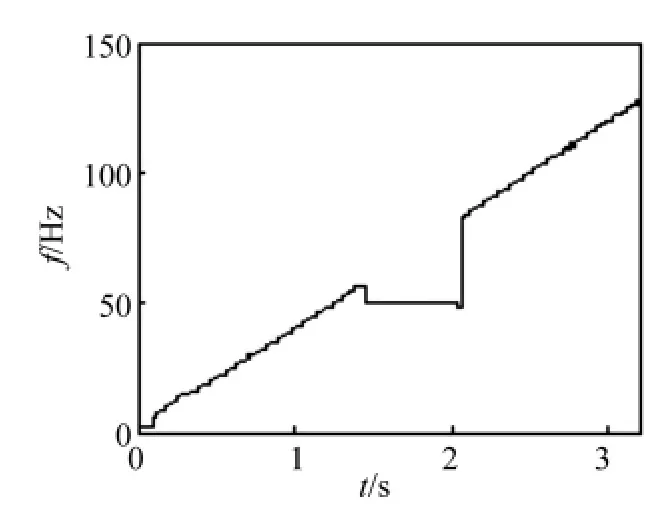
图2 传统峰值搜索法瞬时频率Fig.2 Instantaneous frequency calculated with the traditional peak search method

图3 改进峰值搜索法瞬时频率Fig.3 Instantaneous frequency calculated with the improved peak search method

图4 瞬时频率的最小二乘拟合结果Fig.4 Least squares fitting results of Instantaneous frequency

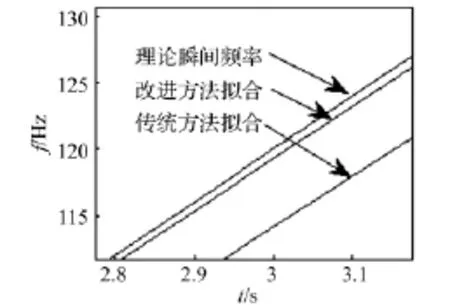
图5 最小二乘拟合结果局部放大图Fig.5 Partial enlargement figure of the least squares fitting results

为便于观察，将图4局部放大见图5。由图5看出，与传统峰值搜索法相比，改进峰值搜索法计算的瞬时频率与理论值更接近。为进一步证明改进方法的有效性，分别计算传统方法提取瞬时频率、改进方法提取瞬时频率与理论瞬时频率偏差:

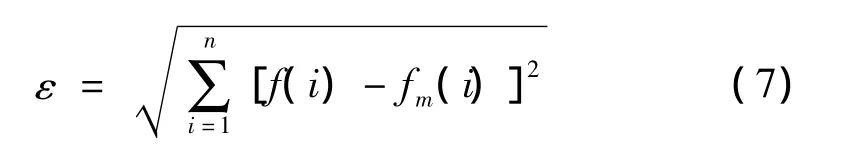
式中:f(i)为理论瞬时频率点，fm(i)为传统方法或改进方法瞬时频率点。经计算，传统方法提取的瞬时频率与理论瞬时频率偏差εt=4.009 Hz，改进方法提取的瞬时频率与理论瞬时频率的偏差εi=1.288 Hz。因此，改进峰值搜索法所取瞬时频率精度高于传统方法。

4 转子升速过程振动信号阶比分析

在Bently转子实验台上进行转子升速过程的油膜涡动实验。转子转速由零逐渐升高，用电涡流传感器测量升速中转子的径向振动，在靠近电机侧转子端部用光电传感器测量转速脉冲信号，采样频率fs=1 280 Hz。以转速n=2 900 r/min为起点，截取转子升速过程中一部分振动信号(图6)进行分析。升速过程振动信号的小波时时频分布见图7。

图6 转子升速过程振动信号Fig.6 Vibration signal of rotor speeding up process

图7 转子升速过程振动信号小波时频分布图Fig.7 Wavelet time-frequency diagram of vibration signal during rotor speeding up

图8 转子升速过程瞬时频率Fig.8 Instantaneous frequency of rotor speeding up process

对转子升速过程的振动信号进行阶比分析。采用改进的峰值搜索法计算转子的瞬时频率，并利用光电传感器采集脉冲信号计算转子瞬时频率，两种方法所得结果如图8所示。由图8看出，改进峰值搜索法提取的一阶瞬时频率与利用脉冲信号计算结果基本吻合。将改进峰值搜索法提取的一阶瞬时频率进行积分获取等角度采样健相时标，并据该时标对原始振动信号进行等角度差值采样，采样间隔0.1 rad。

等角度采样结果如图9所示。对采样结果进行FFT变换，所得阶比谱如图10所示。由图10看出，一阶转频幅值最突出，且0.47阶转频幅值较大。0.47阶转频成分的出现验证了转子升速过程中油膜涡动的发生。

图9 转子升速过程等角度采样结果Fig.9 Sampling results at constant angle increments during rotor speeding up

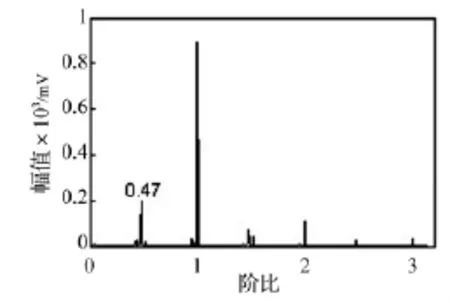
图10 转子升速过程振动信号的阶比谱Fig.10 Order spectrum of vibration signal during rotor speeding up

采用改进峰值搜索法对转子升速过程振动信号进行阶比分析取得良好效果，验证了改进峰值搜索法提取一阶转频的有效性。

5 结论

本文提出用于提取转子瞬时频率的改进峰值搜索法，并应用于旋转机械阶比跟踪。对仿真信号分析结果表明，改进峰值搜索法在提取瞬时频率时能降低干扰信号影响，提取瞬时频率效果优于传统峰值搜索法。通过利用改进峰值搜索法对转子升速过程油膜涡动故障信号进行阶比分析，准确识别出油膜涡动的特征频率，验证了改进峰值搜索法的有效性。

［1］郭 瑜，秦树人，汤宝平，等.基于瞬时频率估计的旋转机械阶比跟踪［J］.机械工程学报，2003，39(3):32-36.

GUO Yu，QIN Shu-ren，TANG Bao-ping，et al.Order tracking ofrotating machinery based on instantaneous frequency estimation［J］.Journal of Mechanical Engineering，2003，39(3):32-36.

［2］Potter R.A new order tracking method for rotating machinery［J］.Sound and Vibration，1990，24(9):30-34.

［3］Fyee K R，Munck E D S.Analysis of computed order tracking［J］.Mechanical Systems and Signal Processing，1997，11(2):187-205.

［4］郭 瑜，秦树人，梁玉前.时频分析阶比跟踪技术［J］.重庆大学学报，2002，25(5):17-20，24.

GUO Yu，QIN Shu-ren，LIANG Yu-qian.Order tracking method based on time-frequency analysis［J］.Journal of Chongqing University，2002，25(5):17-20，24.

［5］杨志坚，丁 康，杨 茜.基于频谱校正理论的阶比跟踪分析［J］.机械工程学报，2009，45(12):41-45.

YANG Zhi-jian，DING Kang，YANG Xi.Novel method of order tracking analysis based on spectrum correction［J］.Journal of Mechanical Engineering，2009，45(12):41-45.

［6］赵晓平，赵秀莉，侯荣涛，等.一种新的旋转机械升降速阶段振动信号瞬时频率的估计算法［J］.机械工程学报，2011，47(7):104-108.

ZHAO Xiao-ping，ZHAO Xiu-li，HOU Rong-tao，et al.A new method for instantaneous frequency estimation of run-up or run-down vibration signal for rotating machinery［J］.Journal of Mechanical Engineering，2011，47(7):104-108.

［7］冯志鹏，刘 立，张文明，等.基于小波时频框架分解方法的滚动轴承故障诊断［J］.振动与冲击，2008，27(2):110-114.

FENG Zhi-peng，LIU Li，ZHANG Wen-ming，et al.Fault diagnosis of rolling element bearings based on wavelet timefrequency frame decomposition［J］.Journal of Shock and Vibration，2008，27(2):110-114.

［8］邹 剑，陈 进，蒲亚鹏，等.转子裂纹仿真研究中的小波时频分析方［J］.应用力学学报，2002，19(4):10-13.

ZOU Jian， CHEN Jin， PU Ya-peng， et al. Simulation research on wavelet time-frequency analysis algorithm in identification of rotor crack［J］.Journal of Applied Mechanics，2002，19(4):10-13.

［9］ Zou J，Chen J，Pu Y P.Wavelet time-frequency analysis of torsional vibrations in rotor system with a transverse crack［J］.Computers and Structures，2004，82(15-16):1181-1187.

［10］唐海英，栾军英，郑海起，等.基于阶次跟踪和经验模态分解的滚动轴承包络解调分析［J］.机械工程学报，2007，43(8):119-122.

TANG Hai-ying，LUAN Jun-ying，ZHENG Hai-qi，et al.Envelope demodulation analysis of bearing based on order tracking and empirical mode decomposition［J］.Journal of Mechanical Engineering，2007，43(8):119-122.