平板断面颤振过程中能量输入特性研究

贾明晓，刘祖军，，杨詠昕

(1.华北水利水电学院 土木与交通学院，郑州 450011;2.同济大学 桥梁工程系，上海 200092)

数值方法与计算机技术进步提升了对颤振本质的认识，已能较准确预测桥梁颤振的临界风速、颤振频率及颤振形态。颤振属自激振动，其物理机理可从能量角度进行阐释。处于气流中桥梁的能量反馈机制表现为气流输入结构—气流系统中能量与结构阻尼耗散能量之间的平衡关系。当输入结构—气流系统中能量小于结构阻尼耗能时，结构在初始扰动下将作衰减(阻尼)振动;而当输入能量大于结构阻尼耗能时结构在初始扰动下将作发散振动;两者相等时结构在初始扰动下将作等幅简谐振动。

对桥梁自激振动能量分析，Scanlan［1］最早提出桥梁颤振的多模态分析方法，并从能量观点对桥梁颤振稳定性进行研究，给出一个振动周期内气流沿桥梁断面每延米输入的总能量与结构耗能表达式，但此仅为理论框架，如何从能量角度对桥梁进行颤振分析，并未给出具体方法。Larsen［2］以CFD方法为基础，据离散涡计算中涡旋运动规律提出简化分析模型。该模型描述桥梁断面扭转运动一个周期内涡旋的运动情况，并通过积分估算由涡旋产生的气动力对桥梁断面所做总功，用能量方法分析涡激力做功与结构稳定之关系。文献［2］颇具开创性，但其计算模型假定在旋涡沿横截面移动时，旋涡升力保持不变且结构阻尼为零，此与实际情况有很大不同。刘高［3］从结构与气流系统内部能量平衡观点对系统颤振进行研究，发展一种全桥多模态颤振分析方法-能量法，通过建立系统等效阻尼比与系统能量变化率之间的关系，推导出系统及各阶模态等效阻尼比计算方法，并据不同风速下系统能量变化率判断系统颤振稳定性。但该方法不能分析气流与结构间的细观作用，尤其结构自激振动中系统能量分布及转化情况。

在机翼气动弹性力学研究中，Frazer［4］分析了维持机翼强迫振动所需的能量条件;Nissim［5］提出气动能量概念作为对机翼主动控制的理论基础;Jones［6］分析颤振发生的能量特征;Carta［7］提出用于颤振失稳预测的能量稳定判据;Klose等［8］通过研究证明能量法用于颤振失稳的预测被认为特征值法在叶片高质量比下的特殊应用，并指出用能量法预测的失效情况。

本文通过风洞试验研究平板的流线断面颤振性能，基于流固松耦合的计算策略，利用现有流体软件的用户自定义(UDF)功能及CFD数值方法，模拟平板颤振过程，据分块分析思想研究颤振过程中振动模型表面不同区域吸收气流能量特点，分析旋涡非定常演化对模型表面不同区域压力特性影响。

1 平板断面风洞测振试验

1.1 平板风洞测振试验及结果分析

风洞试验在同济大学土木工程防灾国家重点实验室TJ-4边界层风洞中进行，该风洞为低速回流式风洞，测振试验段尺寸为:宽 0.814 m，高 0.8 m，长 2.0 m，设计最大试验风速30 m/s。平板断面风洞测振采用模型如图1所示，纵向长度0.8 m。为保证轻质高强，材料采用碳纤维材质。

图1 平板模型(单位:mm)Fig.1 The model of plate(unit:mm)

模型的基本参数:m=1.525 kg/m，Im=0.010 28 kg/m，竖向频率fh=2.588 Hz，扭转频率fa=5.026 Hz。用激光位移计记录模型试验风速下位移信号。

在平板测振试验中，记录的各级风速下结构位移响应结果见图2、图3。风速小于18 m/s时结构位移振幅较小，基本处于静止状态，风速超过18 m/s后结构振动位移值及方差突然增大，竖向振动参与程度不断增加，直之风速达20.4 m/s时结构出现颤振失稳现象。

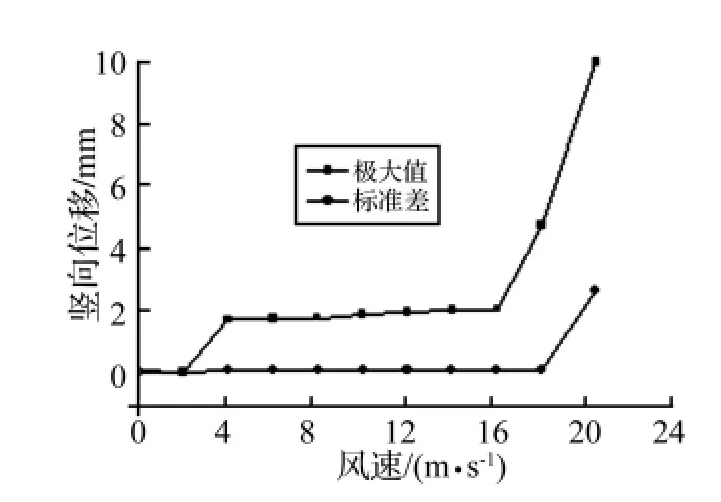
图2 竖向位移随风速变化关系Fig.2 Vertical vibration displacements vs wind velocity curve

图3 扭转振动位移响应-风速曲线Fig.3 Torsional vibration displacement vs wind velocity curve of plate section

图4 位移幅值谱(20.4 m/s)Fig.4 Displacement amplitude spectrum(20.4 m/s)

2 颤振过程的数值模拟

2.1 平板颤振数值模拟方法

气动弹性问题具有重要研究价值，当桥梁结构与空气存在相对运动时，桥梁结构会受到气动力作用，气动力会导致结构位置及形状发生改变。结构位形的改变引起流体占据实际空间发生变化，反过来又导致作用在结构上气动力改变形成流体与固体的相互耦合作用。桥梁的颤振发散也是流固耦合作用的结果。

处理流固耦合问题可采用强耦合与松耦合两种方法。强耦合求解方法以求解流体运动的迭代过程为主，将物体运动的求解耦合在流体运动求解中;松耦合方法为在每个时间步内分别对流体与结构依次求解，通过中间平台交换数据信息，实现两个场的耦合求解。此方法对计算机硬件要求不高，且可充分发挥CFD(Computational Fluid Dynamics)计算与CSD(Computational Structural Dynamics)计算的各自优点，能实现数值计算模块化［9］。分析桥梁结构风致振动问题时多采用松耦合的计算策略。

本文采用松耦合计算方法，用现有商业软件fluent提供的基于ALE(Arbitrary Lagrange Euler)方法的动网格技术，实现颤振数值模拟，通过软件用户自定义函数描述模型及周围气流的刚体运动，颤振数值模拟过程具体步骤为:

(1)进行流体域内固定断面的非定常绕流计算，提取静止状态下初始流场及作用在断面上的三分力，获得t时刻气动力。

(2)据计算所得升力、升力矩，通过数值方法对振动结构进行结构动力学求解。据newmarkk-β方法求解竖向及扭转振动方程，获得t+Δt时刻结构运动的竖向速度与扭转速度:

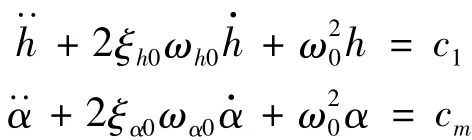
(3)将模型振动速度赋值给包围模型断面并随模型一起做刚体运动部分流体区域，通过fluent提供的用法自定以函数(UDF)描述模型及周围流体运动，采用动网格方法进行流体域求解，获得振动断面气动升力及升力矩。

(4)重复(2)、(3)步，获得桥梁断面振动响应时程。

(5)据断面响应时程曲线判断振动是否已发散，若已发散则该风速即为颤振临界风速，否则增加风速按(1)～(4)步重新计算直到振动发散。

具体计算流程如图5所示。

2.2 颤振数值模拟结果分析

数值模拟用商业软件Fluent提供的RANS方法的k-ωSST两方程模型，计算域大小参考同济大学土木工程防灾国家重点试验室TJ-4风洞中段试验端设置，计算域沿流线长度为3 m(上游1 m，下游2 m)，横向宽度0.8 m。计算时壁面附近最小网格尺度为0.000 4 m，计算域用分块结构化网格。网格数量16.2万。

计算参数设置:动量、湍动能、能量耗散均采用两阶迎风格式进行离散，压力速度耦合采用SIMPLE算法，求解器采用分离式，计算模式选用两阶隐式。边界条件设定:速度入口，湍流强度0.5%，压力出口，计算域上、下端设为对称边界条件，表面采用无滑移的壁面条件。

采用数值方法对颤振过程进行模拟及预测，数值模拟获得该平板颤振临界风速为21.2 m/s与试验结果20.4 m/s尚有一定差距。图6～图8为平板运动时程及幅值谱，数值模拟所得颤振频率为4.73 Hz，实测颤振频率为 4.59 Hz。

图5 颤振数值模拟流程图Fig.5 The process of flutter numerical simulation

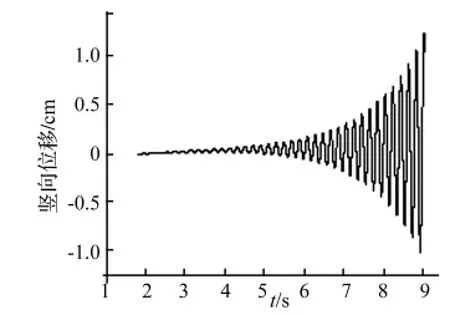
图6 竖向振动位移时程响应(20.4 m/s，CFD数值模拟)Fig.6 Vertical vibration displacement vs time curve of plate section(20.5 m/s，CFD)

图7 扭转振动位移时程响应(20.4 m/s，CFD 数值模拟)Fig.7 Torsional vibration displacement vs time curve of plate section(20.4 m/s，CFD)

图8 位移幅值谱(20.4 m/s)Fig.8 Displacement amplitude spectrum(20.4 m/s)

3 基于分块分析的颤振过程能量分析

3.1 分块分析能量计算方法

分块分析主要为详细捕捉表面压力变化，寻找引起颤振发散的主要能量输入特点，考虑尾部旋涡对气流能量输入方式影响及影响范围。对断面分区，分别计算不同区域的能量输入特点。单位区域能量为单位面积上一个周期内气动力输入到系统的能量，其计算式为:

面积为S(图9的网格线部分)的区域气动力输入能量w(s，t)计算式为:

式中:P(x，t)为结构表面压力，v(x，t)为结构运动速度，n(x，t)为压力与速度夹角。

图9 分块分析示意图Fig.9 The block analysis

据本文提出的分块分析思路编制计算程序，通过提取数值计算获得的模型表面压力，详细研究一个周期内气流向结构输送能量过程，对模型表面进行分区见图10。

图10 模型表面分区Fig.10 The partition of the model

图11～图14为平板扭转振动时不同分区输入到系统的能量。第1区域在前半个周期内上表面消耗能量，下表面吸入能量，后半个周期则反之。一个完整周期内输入到系统的能量为正，但数值较小。从上下表面输入到系统能量随时间变化关系曲线上可看出，输入的能量周期性明显，如图11所示。第4区域输入系统的能量特点与1区基本相似，能量输入也具有周期性特点，二者不同之处在于第4区域消耗系统能量。由于第4区及第1区靠近尾涡，因此受到尾部旋涡的周期性运动影响，该两区域的能量输入具有明显的周期性特征(图14)。

第2区域为系统提供了较多能量，在整个振动过程中下表面始终输入正能量，上表面在前1/4周期消耗能量，后3/4周期内吸入能量，总能量为正，数值较大，且增加较快，见图12。第3区域即风嘴部位为扭转系统最主要能量来源，在一个完整周期内上下表面均吸入系统能量(图13)，且该区域吸入的能量远大于其它区域对系统能量的贡献，为引起结构振动发散的主要能量源。从第2、3区域能量随时间变化关系曲线上可看出，该两部位能量输入周期性不明显，受尾部旋涡运动影响较小。

竖向振动主要能量输入则主要由第2区域引起，见图15，各分区对扭转振动能量的贡献如图16所示。通过上述分析知，风嘴为扭转振动的主要能量输入部位，对系统扭转振动稳定性起重要作用，见图17。

图11 扭转运动1区能量随时间变化关系Fig.11 The energy of torsion in the first partition vs.time curve

图12 扭转运动2区能量随时间变化关系Fig.12 The energy of torsion in the second partition vs.time curve

图13 扭转运动3区能量随时间变化关系Fig.13 The energy of torsion in the third partition vs.time curve

图14 扭转运动4区能量随时间变化关系Fig.14 The energy of torsion in the fourth partition vs.time curve

图15 各分区扭转振动能量随时间变化关系Fig.15 The energy of torsion in every partition vs.time curve

图16 各分区竖向振动能量随时间变化关系Fig.16 11 The energy of vertical in every partition vs.time curve

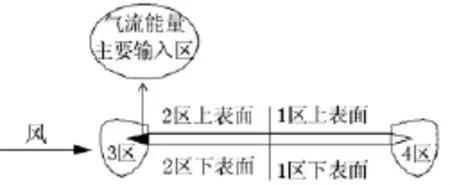
图17 气流能量输入图Fig.17 The energy input by air

3.2 颤振过程旋涡演化对模型不同区域压力特性影响

通过对CFD数值模拟计算结果研究分析发现平板流线型好的断面周围旋涡较难识别，由于振动模型周围流场千变万化，即使模型振动到同一位置，其周围流场也完全不同。因此先用相位平均方法［10］得出模型振动4分点相位的流场图，后用Snapshot POD旋涡识别方法［11］重建流场，所得流场特征见图18。

由数值模拟结果看出，平板因流线型较好，振动模型周围流场中旋涡识别较困难。据POD流场分解结果，平板处于颤振临界状态时，其尾部旋涡形状为较规则圆形，旋涡涡心位于同一高度，呈直线排列，涡街结构较稳定，随着模型振动而发生摆动，但涡心连线基本保持在同一条直线上。

由4区域输入至系统扭转振动能量随时间的变化关系可推测出尾部旋涡对气流输入系统能量的影响。靠近尾流区域受尾部旋涡运动规律作用，输入系统的能量周期性特点明显。为更详细研究尾流运动对结构振动的影响，图19给出4区域上下表面压力分布随时间的变化关系。为清楚说明尾部旋涡对模型不同部位影响，定义上下表面压力差的相对变化量为:=(CPu-CPd)/CPu，其中CPu，CPd为模型上下表面压力最大值。4区域上下表面的相对压力差为:(4)=2.21，(1)=1.61，(2)=1.11，(3)=0(图20)，由此看出，越靠近尾流区域，上下表面压力差值的相对值越大，第4分区最大，而距尾流区最远的第3分区上下表面之间的压力相对差较小，两曲线基本重合。即越靠近尾流区域，其表面压力变化特点与尾流旋涡运动规律越接近。平板振动时尾部旋涡成直线排列并随平板一起做大幅振动，会造成接近尾流区域的表面压力相对变化较大，而远离尾流区域影响较小。

图18 平板断面旋涡驱动结构运动流(颤振风速20.4 m/s，数值模拟)Fig.18 Vortex driven structural movement of plate section(20.4m/s，CFD)

图19 平板表面4个分区上下表面压力随时间变化关系Fig.19 Four regional of plate girder surface pressure vs.time

图20 平板表面4个分区上下表面相对压力差波动系数Fig.20 The volatility coefficient of relative pressure difference on the four model surface regional

4 结论

本文通过风洞试验测试了流线型较好平板断面的颤振性能，采用CFD数值计算方法，并基于流固松耦合计算策略模拟了平板颤振过程，结合分块分析思路定量研究气流对振动模型表面不同区域的能量输入特点及其对模型不同部位表面压力影响，结论如下:

(1)分块分析计算结果表明迎风端风嘴是扭转振动能量的主要输入部位，对系统扭转振动稳定性起重要作用;气流输入到平板的主要能量在一个周期内不断增加，导致平板颤振多为突然性失稳。

(2)由分块分析结果知，模型尾部风嘴处旋涡对气流能量输入方式影响较大。平板处于颤振状态时，尾部受旋涡的直接作用。尾端风嘴处稳定的涡街可控制模型尾端自由振动，使模型尾端运动与涡街摆动趋势基本同步;尾部涡街摆动的规律性，造成模型靠近尾流区域能量输入方式周期性明显;而迎风端的规律性较差，周期性不太明显。

(3)分块分析的结果表明平板尾部规律性摆动的涡街控制结构运动，造成尾部风嘴区域上下表面压力相对波动较大，而远离尾流区域影响较小，其上下表面压力波动程度相对较小。

(4)平板颤振过程中在模型尾部产生的旋涡尺度较小，形态基本为圆形，气流的能量分布在该尺度相当的旋涡之间，当模型振动到平衡位置时，涡街位于同一高度，然后随着模型的振动涡街发生相应摆动，而涡心连线基本保持直线。

［1］Scanlan R H.The action of flexible bridges under wind，Ⅰ:flutter theory［J］.J.of Sound and Vibration，1978，60(2):187-199.

［2］ Larsen A.Aerodynamics of the tacoma narrows bridgc-60 years later［J］.Joumd of Structural Engineering International，2000，10(4):243-248.

［3］刘 高.大跨度悬索桥颤振分析的能量法［J］.中国公路学报，2000，12(3):20-24.

LIU Gao.Flutter analysis of long-span suspension bridges by energy method［J］.China Journal of Highway and Transport，2000，12(3):20-24.

［4］Frazer R A.On the power input required to maintain forced oscillations of an aeroplane wing in flight［M］.ARCR＆M，1939.

［5］Nissim E.Flutter suppression using active controls based on the concept of aerodynamic energy［M］.NASA TND 6199，1997.

［6］Jones J G.On the energy characteristics of the aerodynamic matrix and the relationship to possible flutter［R］.The Aeronautical Quarterly，Part 3，1983:212-225.

［7］ Carta F O.Coupled blade-disk-shroud flutter instabilities in turbojet engine rotors［J］.Journal of Engineering for Power，1967，89(3):419-426.

［8］Klose A，Heinig K.A comparison of flutter calculations based on Eigenvalue and energy method［R］.AD-A2119741，1989.

［9］ Lubcke H，Schmidt S，Rung T，et al.Comparison of les and rans in bluff-body flows［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89(14-15):1471-1485.

［10］ Fujisawa N，Takeda G，Ike N.Phase-averaged characteristics of flow around a circular cylinder under acoustic excitation control［J］.Journal of Fluids and Structures，2004，19(2):159-170.

［11］ Berkooz G，Holmes P，Lumley J L.Proper orthogonal decomposition in the analysis of turbulent flows［J］.Annual Review of Fluid Mechanics，1993，25:537-550.