电梯悬挂系统在建筑摇晃引起位移激励下横向振动分析

王 文，钱 江

(同济大学 结构工程与防灾研究所，上海 200092)

随着城市建筑高度的不断增加，电梯已成为不可或缺的垂直交通运输工具，对电梯运行速度要求越来越快。高层建筑在风荷载与地震作用等水平荷载作用下，会产生或大或小的摇晃，从而引起电梯悬挂系统振动，严重影响电梯乘坐的舒适与安全。电梯悬挂系统振动包括沿轴线方向的纵向振动与垂直轴线方向的横向振动。研究表明高速运行电梯受到外界横向激励时，绳索的横向振动远大于纵向振动，是影响乘坐舒适性和运行安全性的主要因素［1］。国内外对电梯悬挂系统的横向振动已有大量研究。Terumichi等［2］研究在恒定速度下变长度提升系统的非稳态振动现象;Zhu等［3-8］研究运行电梯悬挂系统的横向自由振动及振动主动控制、试验模拟、外部激励下受迫响应;杜小强等［9］引入非线性时变元模型，对曳引绳—轿厢系统非线性水平振动进行研究;Kimura等［10］应用波动法，得到不变张力、恒定速度运行电梯绳索受迫振动的理论解。

本文主要研究高速运行电梯悬挂系统在建筑物摇晃引起的外部位移激励作用下横向振动响应。将高层建筑简化为悬臂梁，设建筑物按基本振型振动。应用Hamilton原理，建立电梯悬挂系统在受两点位移激励时的横向振动偏微分方程，应用Galerkin方法将其离散化为常微分方程组进行求解，得到电梯悬挂系统在不同激励频率下的位移响应，并研究轿厢弹簧刚度、集中阻尼及绳索分布阻尼变化对振动的影响。

1 悬挂系统的横向振动模型

竖向运行电梯悬挂系统可简化为下端附有一定质量的变长度纵向运动张紧绳，如图1所示。电梯轿厢用附加在绳索下端质量为me的刚体表示，假定其通过刚度为ke的弹簧、阻尼系数为ce的粘滞阻尼器与导轨相连，在高度为L的高层建筑中竖向运行。设绳索单位长度质量为ρ，弹性模量为E，绳索时变长度为l(t)。在电梯系统竖向运行过程中，曳引绳上x(t)处的横向振动位移为y(x，t)。

假设建筑结构按基本振型Φ(z)振动，顶点处振动用f(t)表示。则悬臂结构基本振型为:

图1 电梯悬挂系统模型Fig.1 Model of elevator hoisting system

令悬臂结构振动引起电梯悬挂系统上、下端位移激励分别为e1(t)，e2(t)［l(t)，t］，有:

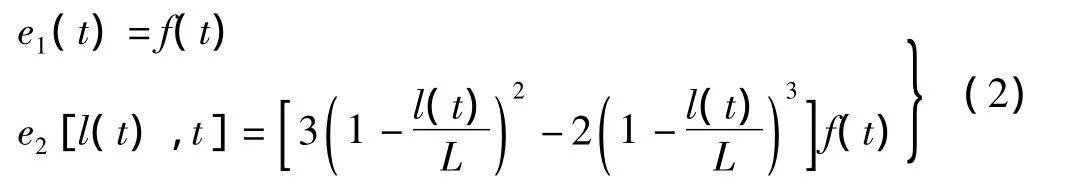
绳索系统动能为:

式中:微分算子:

绳索系统势能为:

式中:P(x，t)为绳索纵向张力:

阻尼力虚功为:

据Hamilton原理:

将式(3)、式(5)、式(7)代入式(8)，应用变分原理与分部积分方法简化可得绳索横向振动控制方程为:

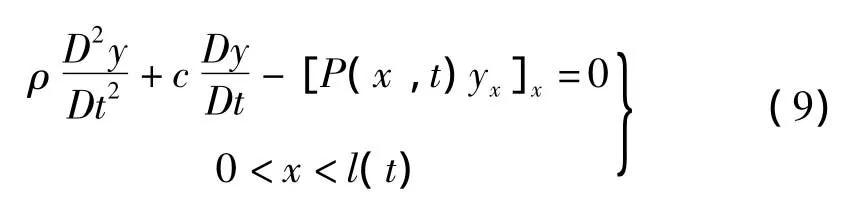
其边界条件为:

式(9)可转化为具有齐次边界条件方程。横向振动位移y(x，t)可表示为:

式中:u(x，t)为满足相应齐次边界条件部分，h(x，t)为不满足齐次边界条件部分。

将式(12)分别代入式(9)～式(11)得:

设h(x，t)可表示为一阶多项式，即:

式中:a0(t)=e1(t)，a1(t)=e2［l(t)，t］-e1(t)。

将式(16)代入式(13)、式(15)，得新的外部激励下偏微分方程组，解出u(x，t)后据式(12)可得绳索系统横向振动位移。

2 偏微分方程离散化求解

引入变量ξ=x/l(t)，将对x时变积分区域［0，l(t)］转化成关于ξ的定积分区间(0，1)。设(ξ，t)=u(x，t)，则u(x，t)对x，t的偏导数及(ξ，t)对ξ，t的偏导数存在关系为:

同理，令(ξ，t)=h(x，t)，则h(x，t)对x，t的偏导数及(ξ，t)对ξ，t的偏导数存在同样关系。

设:

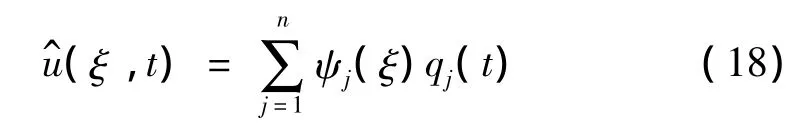
式中:qj(t)为广义坐标，ψj(ξ)为假设振型函数，n为振型数。

据文献［8］，ψj(ξ)可表示为:

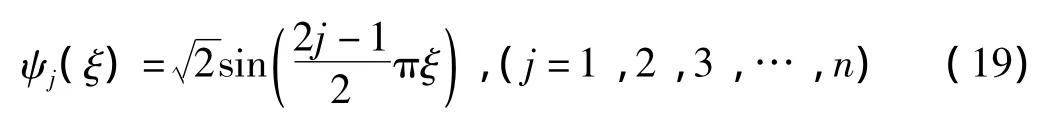
将式(18)、(19)代入式(13)、式(15)，再乘以ψi(ξ)(i=1，2，3，…，n)，并在ξ=［0，1］内积分，将偏微分方程离散化成常微分方程:

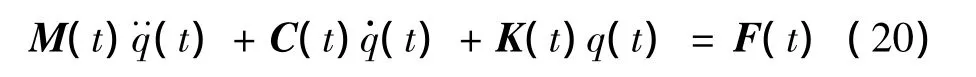
式中:M(t)，C(t)，K(t)，F(t)分别为质量矩阵、阻尼矩阵、刚度矩阵、广义力矩阵。各矩阵元素Mij，Cij，Kij，Fi的表达式分别为:

对式(20)进行逐步积分，可得不同时刻广义坐标q值，代入式(18)、式(12)可得横向振动位移y(x，t)。

3 算例与讨论

本文用文献［8］中典型高速电梯参数进行计算:ρ=1.005 kg/m，me=756 kg，ke=2 083 N/m，轿厢固有频率ωe=1.66。设电梯系统初始条件为静止状态，即y(x，0)=0，yt(x，0)=0。电梯上升过程中位移、速度、加速度及加加速度曲线如图2所示。设建筑物顶部位移激励为f(t)=Z1sin(ω1t)，其中Z1=0.1 m。数值计算所取振型数均为n=20。

图2 电梯上行运行曲线Fig.2 Upward movement profile of the elevator

图3为不同频率激励下轿厢上方10 m处曳引绳无阻尼横向振动位移响应，在远小于绳索基本频率低频激励下，横向振动最大振幅很小，绳索振动频率与激励频率近似相等。当激励频率等于轿厢自振频率时，恰好在绳索基本频率变化范围内，三者产生共振，绳索最大振幅突然增大，振动频率近似等于激励频率。随激励频率的增大，离开共振区绳索最大振幅迅速减小后逐渐增大。图中也可看到，随高速电梯的不断上升，绳索振动幅度及振动频率逐渐加大，此为造成乘员在该阶段的不适及听到嗡鸣声原因。

图4为激励频率ω1=1.66时轿厢上方10 m处曳引绳无阻尼横向振动位移随轿厢刚度变化情况。当ke增大时，绳索振动离开共振区，位移响应迅速减少;随ke的不断增大，位移响应缓慢增加。

由图3、图4可知，无阻尼情况下绳索振动幅度远大于激励位移幅度，而实际工程中是不允许出现的。图5、图6为分别考虑集中阻尼、分布阻尼变化对绳索振动位移影响。图5(a)、图6(a)为绳索系统处于共振情况，从图中看到随集中阻尼、分布阻尼的增大，绳索位移响应逐渐减少;图5(b)、图6(b)为绳索系统处于非共振情况，集中阻尼变化对绳索响应位移基本未产生作用，但分布阻尼微小增加能迅速有效减少绳索的响应位移。

图3 不同激励频率(rad/s)的绳索横向振动Fig.3 Transverse vibration of rope with different frequencies excitations(Unit:rad/s)

图4 不同弹簧刚度(N/m)的绳索横向振动Fig.4 Transverse vibration of rope with different spring stiffness(Unit:N/m)

图5 集中阻尼(N·s/m)对绳索横向振动影响Fig.5 Effect of lumped damping(Unit:N·s/m)on Transverse vibration of rope

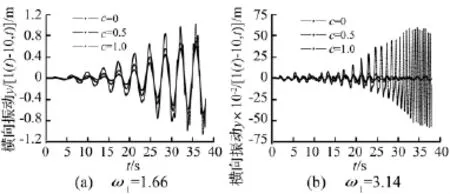
图6 分布阻尼(N·s/m2)对绳索横向振动影响Fig.6 Effect of distributed damping(Unit:N·s/m2)on Transverse vibration of rope

4 结论

通过对建筑物摇晃致高速运行电梯悬挂系统产生横向振动响应分析及算例计算，结论如下:

(1)电梯上行过程中，曳引绳的横向振动幅度与振动频率增大;尤其当激励频率、绳索自振频率与轿厢固有频率接近时，会产生共振，导致轿厢剧烈振动，造成乘坐不舒适感甚至轿厢脱轨。改变轿厢弹簧刚度可改变其固有频率，避免共振发生，能有效减少绳索振动幅度。

(2)发生共振时，增大分布阻尼与集中阻尼均能可不同程度减少绳索振动;在非共振区，增大集中阻尼不能改变绳索振动幅度，但分布阻尼的少许增大能迅速有效减小绳索振动幅度。

(3)本文对高速运行电梯悬挂系统在确定性两点位移激励下横向振动响应分析，为研究电梯悬挂系统在随机位移激励下的动力响应与振动控制提供参考。

［1］张 鹏，朱昌明，张梁娟.变长度柔性提升系统纵向—横向受迫耦合振动分析［J］.工程力学，2008，25(12):202-207.

ZHANG Peng， ZHU Chang-ming， ZHANG Liang-juan.Analysis of forced coupled longitudinal-transverse vibration of flexible hoisting systems with varying length［J］.Journal of Engineering Mechanics，2008，25(12):202-207.

［2］Terumichi Y，Ohtsuka M，Yoshizawa M.Nonstationary vibrations of a string with time-varying length and a massspring system attached at the lower end［J］.Nonlinear Dynamics，1997，30(12):39-55.

［3］Zhu W D，Ni J.Energetics and stability of translating media with an arbitrarily varying length［J］.Journal of Vibration and Acoustics，2000，122(7):295-304.

［4］Zhu W D，Xu G Y.Vibration of elevator cables with small bending stiffness［J］.Journal of Sound and Vibration，2003，263(3):679-699.

［5］ Zhu W D，Ni J，Huang J.Active control of translating media with arbitrarily varying length［J］.Journal of Vibration and Acoustics，2001，123(7):347-358.

［6］Zhang C Y，Zhu C M，Lin Z Q.Theoretical and experimental study on the parametrically excited vibration of mass-load string［J］.Nonlinear Dynamics，2004，37(1):1-18.

［7］Zhu W D，Teppo L J.Design and analysis of a scaled model of a high-rise，high-speed elevator［J］.Journal of Sound and Vibration，2003，264:707-731.

［8］Zhu W D，Chen Y.Forced response of translating media with variable length and tension:application to high-speed elevators［J］. JournalofMultibodyDynamics， 2005，219(1):35-53.

［9］杜小强，梅德庆，陈子辰.高速曳引电梯时变元模型与水平振动响应分析［J］.浙江大学学报(工学版)，2009，43(1):148-152.

DU Xiao-qiang， MEIDe-qing， CHEN Zi-chen. Timevarying element model of high-speed traction elevator and its horizontal vibration response analysis［J］.Journalof Zhejiang University(Engineering Science)，2009，43(1):148-152.

［10］Kimura H，Ito H，Fujita Y.Forced vibration analysis of an elevator rope with both ends moving［J］.Journal of Vibration and Acoustics，2007，129(4):471-477.